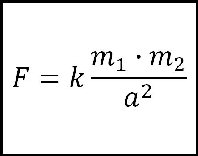I denne oversigt giver vi letforståelige beskrivelser af Keplers love, af Newtons love og af sammenhængen mellem dem. Først

Keplers love Kepler skabte grundlaget for himmelens mekanik: Han fremsatte på grundlag af Tycho Brahes observationer og en tro på Kopernikus´ teori sine tre love: Keplers tre love for planeternes baner: 1. lov: "Baneloven", der siger, at banerne er ellipser med Solen i det ene brændpunkt. 2. lov: "Arealloven" beskriver, hvordan en planet bevæger sig hurtigst, når den er nærmest Solen og langsomst, når den er længst væk fra Solen. 3. lov: "Afstandsloven" siger, at når man sammenligner to planeter, da har den, der er længst væk fra Solen, længere omløbstid end den anden. Tilsammen beskriver de tre love planeternes bevægelser i den forstand at man ud fra lovene kan forudberegne planeternes stilling på himlen. For en nærmere gennemgang, se under "1609 Keplers astronomi".

Så går vi over til at beskrive

Newtons love Newtons love er almengyldige naturlove. Når man specielt anvender dem på planeterne kan man udlede Keplers love. De tre centrale love hos Newton er følgende: A. Gravitationsloven. Den siger, at to legemer tiltrækker hinanden med en kraft. Jo mere legemerne vejer, jo større er kraften. Jo længere de to legemer er fra hinanden, jo mindre er kraften. B. Newtons 2. lov siger, at kraft er lig masse gange acceleration. Tidligere troede man, at når man påvirkede et legeme med en bestemt kraft, ville det få en bestemt hastighed. Newton siger: "Nej, det får en bestemt ændring af hastigheden, dvs. en bestemt acceleration." C. Newtons 3. lov: Når et legeme påvirker et andet med en kraft, så påvirker det andet det første med en lige så stor, men modsat rettet, kraft. Når f.eks. en magnet trækker i et stykke jern, så vil jernet trække lige så meget i magneten, bare den modsatte vej. Newton påviste, at de tre love A, B og C gjorde det muligt, med tilfredsstillende nøjagtighed, både at beregne faldtider her på Jorden og at beregne planetpositioner. Det, Newton påviste, er naturligvis lige så rigtigt i dag, som det var dengang.

Newton og Kepler Af Keplers tre love kan man slutte, at Newtons love må gælde for planetbevægelserne. Og omvendt kan man af Newtons love udlede, at Keplers love må gælde for planetbevægelserne.

Der er altså ialt i alt er 2×3=6 "veje" eller påstande, der skal bevises! De tekniske detaljer i fem af beviserne kan du finde ved at gå til listen under "Newton og Keplers love" og klikke på "Mere". Newton giver i sin Principia (1687) fyldestgørende beviser for disse 5 af de 6 påstande. Men der er én af vejene, som Newton ikke havde helt tjek på. Han prøvede dog at komme med lidt mere udførlige bevisskitser i de senere udgaver af Principia. Påstanden kaldes det omvendte Kepler-problem, og det siger følgende: Et legeme, der bliver tiltrukket mod et fast centrum med en kraft, der er omvendt proportional med kvadratet på afstanden fra centret, må bevæge sig på et "keglesnit" (f.eks. en "ellipse"), der har det ene brændpunkt i dette center.

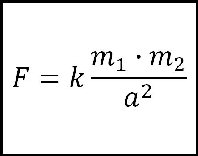Det var først schweizeren Johann Bernoulli (1667-1748), der fandt på et fuldgyldigt bevis for denne 6. "vej" i 1710. Bernoulli var en af Newtons ærkefjende Leibniz´ gode venner. Problemstillingen har helt op til vore dage givet anledning til megen forskning i fysikkens historie, se referencerne.

Hvis du støder på et ord, hvis betydning du ikke kender, så søg på ordet.