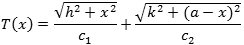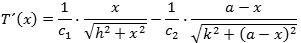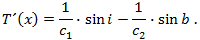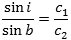Fermat formulerede selv sit princip for lysets brydning meget generelt. Det gælder således også for sollysets brydning i Jordens atmosfære, hvor brydningsforholdet hele tiden ændrer sig. Her vil vi kun beskrive princippet i det simpleste tilfælde, hvor lysets brydes i en plan grænseflade mellem to homogene (dvs. ensartede) medier med forskellige lyshastigheder c₁ og c₂. Fermats eget bevis for princippet er overordentlig kompliceret. Det findes i René Dugas´ bog, se referencerne. 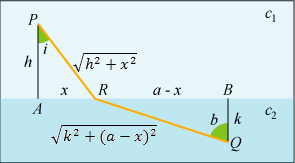Beviset nedenfor benytter differentialregning, som Fermat ikke havde til rådighed. Figuren viser den situation, vi vil betragte.

Vi vælger et punkt P i det ene medium og et punkt Q i det andet, og vi vil finde ud af, hvor på grænsefladen vi skal lægge R, så PRQ bliver den hurtigste vej for en lysstråle fra P til Q. Afstanden mellem punkterne A og B kaldes a, så hvis vi sætter AR = x bliver RB = a - x. Det er intuitivt klart, at der må være en værdi af x, hvor det går hurtigst for lyset at komme fra P til Q. Hvis f.eks. R ligger lige ved siden af A, bliver det bedre, hvis man rykker R et par mm til højre. For det ændrer jo ikke nævneværdigt på afstanden foroven, men forneden sparer man mærkbart. Tilsvarende bliver det hurtigere, hvis man, fra en position lige til venstre for B, rykker R lidt til venstre. Der må så være et eller andet sted derimellem, hvor det går hurtigst, og det sted vil vi nu finde. For en bevægelse med konstant hastighed er tiden lig afstanden divideret med hastigheden. Derfor må den tid, lyset bruger for at gennemløbe stykket PRQ, være

For at finde ud af, hvornår denne funktion har sin mindste værdi, differentierer vi den:

Nu burde vi så finde den værdi af x, for hvilken T´(x) = 0. Det fører imidlertid til et mareridt af besværlige udregninger. I stedet kan man mirakuløst opdage, at de to brøker med x-er ifølge trekanterne på figuren er henholdsvis sin i og sin b. Derfor er

T´(x) er altså 0, når

dvs. når Snells brydningslov i Huygens´ version er opfyldt. Omvendt kan man også se, at hvis lyset følger brydningsloven, da er T´(x) = 0, og lyset går derfor ad den hurtigste vej. Vi har altså vist

Fermat´s princip: En lysstråle gennemløber også under brydning den hurtigste vej mellem to punkter på lysstrålen.

Ovenstående argument er lidt mystisk og lidt overraskende. Vi lader, som om vi er ude efter en x-værdi, men undervejs opgiver vi det og når i stedet frem til, at Fermats princip er ensbetydende med brydningsloven. Og så er vi glade, selv om vi hverken fandt x eller i eller b.

I 1684 skrev Leibniz sin første artikel om differentialregning. Her viste han ved differentiation at man af brydningsloven kan udlede, at lyset under brydning følger den hurtigste vej.

Hvis du støder på et ord, hvis betydning du ikke kender, så søg på ordet.