Forside Søgning Liste

Drejningsmoment

I vores omtale af inertimoment har vi bestemt den kinetiske energi i et legeme, der drejer sig om en akse. Vi går nu over til at beskrive virkningen af kræfter, der påvirker et roterende legeme. En kraft der er parallel med aksen har ingen indflydelse på legemets bevægelse. Det samme gælder om en kraft der ligger på en linje, der skærer aksen. Vi kan derfor nøjes med at betragte kræfter, der er vinkelrette på aksen, og som ikke ligger på en linje, der skærer aksen.

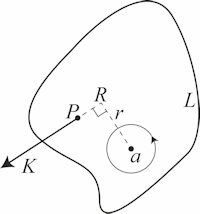
På figuren til venstre er omdrejningsaksen a vinkelret på skærmen. Legemet L er påvirket af en enkelt kraft K, og legemets inertimoment betegnes I. Afstanden fra a til den linje kraften ligger på kaldes r. Produktet H = Kr kaldes kraftens moment, og det har været kendt siden oldtiden, at det er momentet, der bestemmer kraftens virkning. Det følger heraf, at en kraft ikke ændrer sin virkning på legemet, når man forskyder kraftens angrebspunkt til et andet punkt på den linje, som kraften ligger på. Se vores artikel om vægtstangen, der er link foroven. Momentet regnes med fortegn på den måde, at momentet er positivt, når det prøver at dreje legemet den vej, som pilen nede ved a drejer. På figuren er momentet altså positivt, men hvis kraften pegede den anden vej, ville momentet være negativt. Momentet bevirker en ændring af den øjeblikkelige vinkelhastighed ω. I et kort tidsrum fra tidspunktet t til tidspunktet t + Δt ændres vinkelhastigheden fra ω til ω + Δω. I dette korte tidsrum er den kinetiske energi vokset med værdien

½I(ω + Δω)² - ½Iω² = ½Iω² + Iω Δω + ½I(Δω)² - ½Iω² = Iω Δω + ½I(Δω)² = Iω Δω. Her kan Δω godt være negativ.

Her har vi set bort fra leddet med (Δω) ² fordi det er enormt lille i forhold til Iω Δω. Resultatet er, at på Δt sekunder er den kinetiske energi steget med værdien Iω Δω.

Vi går nu over til at beregne det arbejde, som kraften K udfører i de samme Δt sekunder. Vi kan som nævnt antage, at kraften K angriber legemet i det punkt, som R befinder sig i til tidspunktet t. I tidsperioden fra t til t + Δt vil punktet R bevæge sig et stykke i retning af K. Da vinkler måles i radianer (se Vinkelmål, der er link for oven), vil det stykke, R bevæger sig være rωΔt. Derfor vil det arbejde, som Kraften udfører i disse Δt sekunder være K·rωΔt. Da arbejdet er lig med tilvæksten i energi har vi altså, at

K·rωΔt = Iω Δω

Hvis vi kalder drejningsmomentet Kr for H har vi altså, at

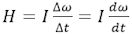
Denne formel er afgørende for den måling af elektrisk tiltrækning og frastødning, som Coulomb udførte i 1785.

Hvis legemet er påvirket af flere momenter, f.eks. H₁, H₂ og H₃ gælder ligningen ovenfor stadig,
når man sætter H = H₁ + H₂ + H₃.

Denne påstand svarer til at for en punktformet masse, der er påvirket af 3 kræfter, er summen af kræfterne masse gange acceleration. Jeg er ikke klar over, hvornår man første gang blev opmærksom på sådanne analogier mellem kræfter, der påvirker et massepunkt, og momenter, der påvirker et legeme, der kan dreje sig om en akse.

Hvis du støder på et ord, hvis betydning du ikke kender, så søg på ordet.