William Herschel var en meget flittig engelsk astronom. Han byggede sammen med sin søster Caroline fremragende teleskoper, og hans arbejder betød et stort fremskridt for astronomien.

1. Herschels teleskoper

I 1781 fandt Herschell planeten Uranus, se link for oven. Det var første gang siden græsk oldtid, at man fandt en ny planet, og fundet vakte opsigt i hele den videnskabelige verden. Inspireret af det, sendte Kong Georg III. bud efter Herschel, og gjorde ham til "hofinstrumentmager". Herschel og hans familie måtte derfor flytte til Windsor, hvor kongen residerede. Til at begynde med gik det dårligt, de havde ikke meget at leve af. Men da Kongen fik det at vide, fik Herschel en kolossal bevilling til bygning af teleskoper.

I det følgende får vi brug for nogle af de resultater, som Ibn al - Haitham fandt vedrørende billeddannelse i hulspejle, der er link for oven.

Til højre viser vi et billede af Herschels største teleskop. Det var 40 fod (dvs. 12 meter) langt, og det havde et spejl, der var 50 tommer (1,25 meter) i diameter. Læg mærke til at det kæmpemæssige apparat hviler på 12 ruller, så det hele, bl.a. hus og teleskop med ophæng, kan drejes om en lodret akse. Teleskopet er ophængt i et laangt tov af stål, som via 6 trisser ser ud til at komme op til den lille platform, som observatoren står på. Der har nok været et håndsving, som observatøren kunne dreje på, når teleskopet skulle hæves eller sænkes. Det fremgår ikke af tegningen om observatoren også kan dreje det hele om den lodrette akse, eller om han skal have hjælp til det af den skyggeagtige figur, der anes nederst i baggrunden. Det er klart at ved fremstillingen af dette store instrument var der brug for en lang række dygtige håndværkere. Til den bærende konstruktion krævedes der mange tømrere. Selve kikkertrøret er af metal, jeg gætter på kobber eller messing. Fremstillingen af røret, har krævet meget kompetente smede.

Som man kan se på billedet er teleskoprøret dobbelt. Den øverste del er tegnet stribet, og den nederste del, som er tegnet grå, har en ydre diameter, der er lidt mindre end den indre diameter af den stribede del. Den stribede del skal så placeres sådan at spejlbilledet af de stjerner man vil iagttage, er få cm væk fra den øverste munding. Herschels teleskoper adskiller sig fra Newtons på tre punkter: For det første er de meget større, Newtons teleskop er kun ca. 20 cm langt. For det andet har Newton et lille skråt spejl øverst i teleskopet, og det sender lyset ud gennem en lup, der sidder i en hul lidt under den øvre mundingsrand. Denne konstruktion udelod Herschel på grund af de billedfejl den bevirkede.

For det tredie sidder spejlet hos Herschel en smule skråt, sådan at billedet af en stjerne, som teleskopet sigter mod, befinder sig få cm inden for mundingsranden. Man kan se strålegangen på billedet til venstre. Så kan den velklædte observator, som man ser på billedet øverst, iagttage stjernen ved at holde hovedet lidt ind foran rørets munding. Pointen i dette er, at observators hoved kun skygger for en meget lille del af det lys, der fra stjernen kommer ind i kikkerten. Den del af synsfeltet, der er godt belyst, er ca 5° bredt. Til sammenligning fylder Månen ½°. Jeg tror ikke, at dette teleskop er særlig egnet til måling af stjernepositioner. Det er sikkert svært at indstille teleskopet, så det sigter præcist på en stjerne, hvis koordinater er kendt. Teleskopet har den store fordel, at lysstyrken af de stjerner, der befinder sig centralt i synsfeltet er kollossal sammenlignet med det blotte øje.

I 1789, kort tid efter at teleskopet var klar til brug, fandt Herschel en hidtil ukendt saturnmåne. Den fik navnet Minas; den er kun 400 km i diameter, så det var noget af en bedrift at få øje på Minas.

Dette store teleskop viste sig trods alt at være meget upraktisk, og de fleste af Herschels følgende iagttagelser blev gjort med mindre teleskoper, især et der var 6 meter langt og ½ meter i diameter. Disse mindre teleskoper var nok bedre end det store til at udføre præcise positionsbestemmelser. Herschell og hans søster Caroline fremstillede mange teleskoper, flere af vores kilder siger i hundrevis.

På billedet til højre viser vi et af de teleskoper, som Herschel brugte meget. Teleskopets spejl har en brændvidde på 2,1 meter, og det adskiller sig på mange andre måder fra Herschels store teleskop. En af forskellene er, at der sidder et skråt spejl inde i den øverste del af teleskopets rør, tæt ved de sted, hvor teleskopets spejl danner billede. Dette billede kan så iagttages gennem en lup, som sidder i et hul foroven i teleskopets rør. Luppen kan anes på billedet. En fordel ved dette arrangement er, at iagttageren ikke behøver at stikke hovedet ind foran den øverste åbning i teleskopets rør. Iagttageren skygger altså ikke for lyset fra stjernerne, men til gengæld skygger det lille spejl for oven en smule. En anden fordel er, at det er simpelt at indstille den astronomiske højde af det iagttagne område. Teleskopet bliver understøttet omtrent på midten, og den nederste ende af teleskopet kan hæves og sænkes med et snoretræk, som anes på billedet. Det ender i et håndsving, som iagttageren kan dreje på under iagttagelsen. Det fremgår ikke af billedet hvordan højden måles, men der må et eller andet sted have siddet en gradskala, som højden kunne måles på. Nær den øverste munding må der have været et trådkors der udgør to på hinanden vinkelrette diametre i mundingen. Den ene diameter skal være vandret. Når Herschel skulle sigte præcist på en stjerne, så skulle stjernen ses, hvor trådene skærer hinanden. Det fremgår ikke tydeligt af billedet hvordan teleskopet står på Jorden. Jeg tror ikke, at der er hjul forneden, det ville gøre observationerne upræcise. Det vil være hensigtsmæssigt, at stille teleskopet sådan, at når teleskopet er vandret, så sigter det præcist mod syd.

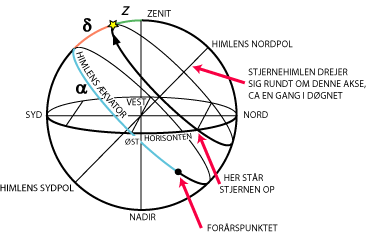Det som Herschel ønskede at beregne var koordinaterne til den stjerne, som teleskopet sigtede på, f.eks. stjernens rektascension α og deklinationen δ, der er link til disse begreber for oven. På billedet til venstre illustrerer vi situationen. For at kunne beregne en stjernes koordinater, var det nødvendigt at Herschel kendte observationstidspunktet i stjernetid, der er link for oven. Så Herschel havde også et 24-timersur, der gik efter stjernetid. Når Herschel skulle bestemme positionen for en bestemt stjerne valgte han at sigte på stjernen på et tidspunkt, hvor stjernen stod i syd, altså havde størst mulig højde, sådan som det er vist på billedet. Da han på uret kan aflæse observationstidspunktet i stjernetid kender han beliggenheden af forårspunktet og dermed den blå rektascension α.

Højden, som Herschel målte var vinklen fra punktet SYD og op til stjernen. Vinklen mellem horisontens plan og Ækvators plan er den geografiske bredde, som for Herschel var 51,5°. Differensen mellem disse to vinkler er den røde deklination δ, som Herschel derfor også kunne beregne.

Vi tænker os nu, at iagttagerens geografiske bredde er b > 0. Hvis vi så flytter stjernen på figuren ned under punktet SYD, vil stjernen hele tiden bevæge sig under horisonten, den vil altså aldrig kunne iagttages. Betingelsen for at en stjerne med deklination δ kan iagttages er altså at δ > -b.

2. Variationer i stjernehimlen

Før Herschels tid blev stjernehimlen stor set betragtet som noget stationært. Men under sine omhyggelige observationer af stjernehimlen opdagede Herschel, at stjernerne bevægede sig i forhold til hinanden. For hver enkelt lysstærk stjerne kunne Herschel måle både den øjeblikkelige position og størrelse og retning af den årlige flytning. Billederne nedenfor viser hvordan de store stjerner i Karlsvognen vil flytte sig i en periode på 36000 år. Det lyder som lang tid, men det er det ikke i forhold til stjernehimlens alder.

Sådan ser Karlsvognen ud i dag,

Pilene viser bevægelsesretningerne

- og sådan vil den se ud om 36000 år

La Cour skriver følgende: "Når man vandrer i en skov hen imod et mål, da ser man træerne derhenne vige til siderne. De, der er til højre for målet, viger til højre, de, der er til venstre, viger til venstre; og trætoppene der henne løfter sig, så vi siden får dem lige over hovedet."

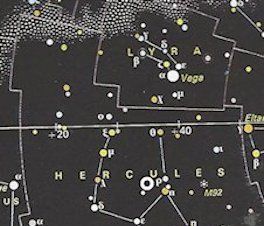
Sådan må det også være, hvis Solen med planeterne bevæger hen mod et punkt på stjernehimlen; så vil stjernene i nærheden af det punkt alle synes at bevæge sig væk fra dette punkt. Og Herschel fandt faktisk sådan et punkt. Det ligger i stjernebilledet Hercules, på stjernekortet til venstre er det markeret med en hvid cirkel, lige under u i Hercules. Naturligvis vil det modsatte punkt på stjernehimlen være sådan, at alle nabostjerner vil bevæge sig hen mod det. Længere nede på stjernekortet i stjernebilledet Herkules ses en animation, der viser, hvordan en dobbeltstjerne kan bevæge sig. Jeg gætter på, at på animationen er banens størrelse overdrevet. Vær opmærksom på, at når man iagttager en langsom bevægelse på animationen, så kan bevægelsen i virkeligheden være meget hurtig, men rettet mod iagttageren. Indtil dette tidspunkt havde astronomerne først og fremmest studeret planeternes og deres måners bevægelser. Herschel selv opdagede to nye måner ved Saturn, og efter at han havde opdaget Uranus fandt han også to måner ved Uranus. Herschels søster Caroline fandt 8 kometer, der ikke havde været iagttaget før.

En af de ting, som Herschel opdagede med sine nye teleskoper, var at antallet af stjerner er langt større end man kunne forestille sig ved iagttagelse med det blotte øje. Uden kikkert kan man se noget i retning af 5000 stjerner på hele himmelkuglen. Men Herschel kunne med sine teleskoper se langt flere.

3. Parallakse

Allerede Tycho Brahe og Rømer beskæftigede sig med begrebet stjerners parallakse. Begrebet illustreres på figuren til højre. Den diameter i Jordens bane, der et vist på figuren er den, der er vinkelret på retningen fra Solen til stjernen. Parallaksen p af stjernen defineres som den vinkel man ser den nævnte diameter under, hvis man opholder sig på stjernen. Jo længere væk stjernen er, jo mindre er dens parallakse. Man behøver nu ikke at tage op til stjernen for at måle parallaksen. Man kan først måle vinklen ST J P og dernæst ½ år senere måle vinklen ST P J , og så udnytte, at vinkelsummen i en trekant er 180°. Tycho prøvede at måle parallaksen, men han fandt, at den måtte være så lille at verdensrummet og stjernerne - efter den tids syn på det - ville være urimeligt store. Han foreslog derfor det tychoniske verdensbillede, hvor Jorden står stille mens Solen med sine 5 andre planeter bevæger sig rundt om Jorden. Tychos målenøjagtighed var ca. en hundrededel af en grad og stjerneparallakserne er alle mindre end 0,0003°, så det var langt under, hvad Tycho kunne måle. Når man kender en stjernes parallakse, kan man let beregne dens afstand.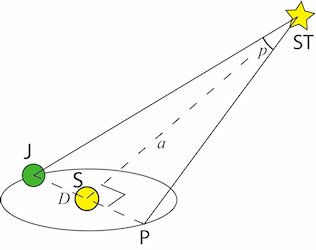

Herschels teleskoper satte nye rekorder, i hvad man kunne se på stjernehimlen. Han prøvede at måle stjerners parallakse, men det lykkedes ikke for ham. Men han gjorde andre interessante opdagelser. Den mest berømte er hans opdagelse af planeten Uranus, som vi her beskriver under 1781 Herschel, der er link for oven. I sit forsøg på at måle en stjernes parallakse brugte Herschel en metode, der vistnok først var foreslået af Galilei:

Ideen er at det kan være meget svært at måle den lille forskydning af en stjernes position, der sker mellem to iagttagelser med ½ års mellemrum. Så vil det være meget lettere at vælge 2 stjerner, der står meget tæt på hinanden på himlen, og som har meget forskellig lysstyrke, sådan som det er vist på billedet ovenfor. Så er det naturligt at antage, at den svage stjerne er meget længere væk fra Jorden end den stærke. Man kan så finde parallaksen for den store stjerne, ved at måle hvordan vinklen mellem de to punkterede linjer varierer i løbet af et år. Synslinjen til den svage stjerne flytter sig nemlig ikke, fordi stjernen er så langt væk. Derfor er det nok at måle, hvordan vinklen mellem de to punkterede linjer varierer i løbet af et år. Det er meget lettere at måle en vinkel mellem to retninger, der kan ses samtidigt, end det er af måle vinklen mellem to retninger, der kan iagttages med ½ års mellemrum.

På den beskrevne baggrund udvalgte Herschel sig en masse stjernepar på himlen, par bestående af en lysstærk og en lyssvag stjerne, der sås i næsten samme retning. For hvert par målte han de to stjerners afstand, og fulgte løbende deres bevægelser i forhold til hinanden. Herschel blev overrasket da han opdagede, at deres bevægelser ikke gentog sig med en periode på et år, som de skulle, hvis der var tale om en parallakse. I stedet opdagede han, at mange af stjerneparrene bevægede sig i forhold til hinanden som de skulle, hvis de kun var påvirket af den indbyrdes tiltrækningskraft. De to stjerner er altså næsten lige langt fra Jorden, og de udgør det, der hedder en dobbeltstjerne. Sådan en dobbeltstjerner beskriver vi nærmere i det følgende afsnit.

4. Dobbeltstjerner

Herschel beskrev 846 dobbeltstjerner, som bevægede sig i elliptiske baner rundt om hinanden. Vores kilde er ikke Herschel, vi har ikke adgang til Herschels stjernekatalog, men Herschel har gjort mange iagttagelser, der minder om den, vi nu beskriver.

Rigel eller α Centauris

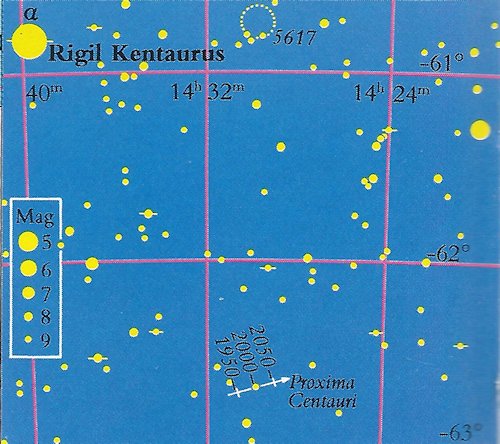Stjernen Rigel ligger i det stjernebillede, der på dansk hedder Tyren. Det er den stjerne, der er nærmest Solen. Lyset, der går 300.000 km/sek, er kun 4,3 år om at nå frem til os. Ikke desto mindre er 4,3 lysår en meget lille afstand set fra universets synspunkt. De to stjerner, som udgør Rigel er kun 9" fra hinanden; 1" kaldet et buesekund , er 1/3600 - del af 1°. Det er så tæt, at man ikke på kortet til venstre har kunnet afbilde begge stjerner. Man kan se dem adskilt i et teleskop. I 1994 var de to stjerner 20" fran hinanden, og man har beregnet at afstanden i 2035 vil være 2", og man har også beregnet, at omløbstiden er 80 år. Det betyder, at stjernerne ses i næsten samme retning, ikke at de er kommet tættere til hinanden. Hvis du nu synes, at det er et mærligt tilfælde, at lige præcis den stjerne er er en dobbeltstjerne, så har du ikke ret. Flertallet af alle stjerner er nemlig dobbeltstjerner. På billedet kan man se, at Rigel har deklinationen - 61°. Den kan altså ikke iagttages fra vores breddegrad, som er 55°. -Beklager!

Herschel fulgte ikke nogen dobbeltstjerne i et helt omløb, men han fulgte mange par så længe, at han kunne beregne omløbstiderne.

Senere blev det opdaget, at de to stjerner, som Rigel består af er ledsager af en tredie stjerne; så i virkeligheden er der tale om en "tripelstjerne". Heller ikke det er usædvanligt. Den tredie stjerne hedder Proxima Centauri, og dens position i 1950, 2000 og 2050 er vist på kortet.

På kortet er der vist yderligere 7 dobbeltstjerner; de er vist som en stjerne med en kort vandret streg igennem.

Det såkaldte tolegemeproblem handler om at beregne banebevægelserne for to legemer, der kun er påvirket af hinandens massetiltrækning, når passende begyndelsesbetingelser samt stjernes masser er givne. Dette problem kan løse ved hjælp af differential- og integralregning. Resultatet er, at med fornuftige begyndelsesbetingelser bliver banerne to ellipser med et fælles brændpunkt og de to stjerners tyngdepunkt ligger i dette brændpunkt. Jeg har ikke kunnet finde ud af, hvem der først løste tolegemeproblemet, men der er intet i vores kilder der antyder, at Herschel kendte løsningen.

Som et eksempel kan vi nævne stjernen ξ i stjernebilledet Karlsvognen. Begge stjerner kan under gunstige omstændigheder ses med det blotte øje Det er den næstyderste stjerne på Karlsvognens vognstang og den stjernes position målte Herschel i 1781, 1803 og 1825, og det fulde kredsløb blev iagttaget i 1842, formodentlig af sønnen John Herschel. På denne baggrund kunne man foretage en komplet baneberegning og konstatere, at Keplers og Newtons love ikke kun gælder for vores sol og planeter, men også ude i Verdensrummet, en opdagelse af fundamental betydning.

I 1780 - erne offentliggjorde Herschel to kataloger over ca 700 dobbeltstjerner. Nogle få af dem viste sig senere ikke at være dobbeltstjerner, men blot tilsyneladende være tæt ved hinanden. Mange af "dobbeltstjernerne" bestod af mere end 2 stjerner, der kunne være 3, 4, 5, ?? stjerner i et sådant system. Det vi iagttager er kun banernes projektioner på en plan vinkelret på retningen til Jorden. Vi kan derfor synes, at banerne er meget aflange ellipser, mens de i virkeligheden kan være tæt på at være cirkulære. Efter William Herschels død fortsatte sønnen John både med observationer og med offentliggørelse af kataloger.

4. Mælkevejen

Øverst på billedet i slutningen af afsnit 2 er der et område, hvor stjernerne ses meget tæt. Det område kaldes Mælkevejen, og den strækker sig som et mælkefarvet bånd hele vejen rundt på stjernehimlen. På billederne herunder viser vi med gråt hvor Mælkevejen kan iagttages mellem stjernerne.

Den nordlige himmel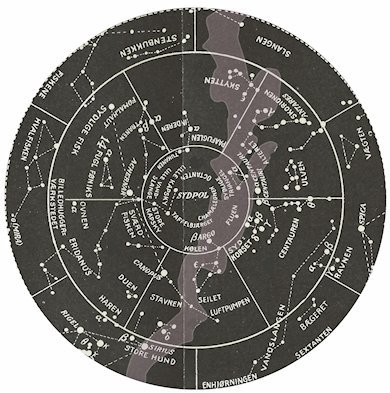

Den sydlige himmel

Til venstre viser vi et moderne fotografi af Mælkevejen. Herschel skønnede at der var 18 millioner stjerner i Mælkevejen, men i dag ved vi, at der er noget i retning af 200 milliarder stjerner i Mælkevejen. Alle de stjerner, vi kan se, tilhører Mælkevejen. Afstandene ud til stjernerne og mellem stjernerne kendte man stadig ikke. Herschel fandt ud af, at Mælkevejen er en flad rund skive bestående af talrige stjerner. Han tænkte sig, at Solen er en af stjernerne i Mælkevejen og at det er Mælkevejens flade form der gør, at den viser sig for os som et lysende bånd på himlen. Han tænkte sig, at alle de stjerner, vi kan se på himlen tilhører Mælkevejen; de er bare dem, der er nærmest ved os.

Herschel prøvede på forskellige måder at finde ud af flere detaljer om Mælkevejens form, men det lykkedes ikke for ham.

5. Stjernehobe og stjernetåger

Herschel var også opmærksom på, at der ud over stjernerne på himlen og Mælkevejen også findes talrige tågeagtige pletter på himlen. Før Herschel kendte man godt 100 sådanne tåger. Herschel opdagede at der var to slags stjernetåger. Der var dels de såkaldte stjernehobe, som i Herschels fremragende teleskoper kunne opløses i enkeltstjerner. Til højre viser vi et billede af sådan en stjernehob. I dag ved vi, at der er ca 150 af disse stjernehobe. De er en del af Mælkevejen, men de befinder sig i et kugleformet omåde, som omkranser resten af Mælkevejen.

Herschel fandt også, at der er en masse tågeagtige objekter på himlen, som han ikke kunne opløse i enkeltstjerner. I 1802 offentliggjorde Herschel et katalog med positioner af 2500 af disse stjernetåger, og i 1820 et katalog med 5000 tåger. I dag ved vi, at disse tåger er er fjerntliggende strukturer, der minder om Mælkevejen. På billedet til venstre viser vi et nutidigt billede af den stjernetåge, der i dag hedder NGC 2683. Herschel opdagede denne tåge den 5. februar 1788.

Hvis du støder på et ord, hvis betydning du ikke kender, så søg på ordet.