Forside Søgning Liste

Mere om Joseph Sauveurs bestemmelser af lydfrekvenser.

Jeg lærte i skolen, at enhver ordentlig fristil skulle begynde med ordene "Allerede de gamle grækere ...". Så ...

Allerede de gamle grækere vidste, at højden af en tone afhang af hvor mange svingninger, der er i lyden hvert sekund. Hvis f.eks. lyden var frembragt af en svingende streng, var det antallet af gange, strengen svingede frem og tilbage hvert sekund, der bestemte tonehøjden. De vidste også, at for en bestemt streng, udspændt af en bestemt vægt, var frekvensen - og altså tonehøjden - omvendt proportional med strengens længde. Derfor vidste de også, at f.eks. oktaven til en tone svinger dobbelt så hurtigt som tonen selv. Der relative værdier af frekvenserne at standardtonerne var altså kendte. Men hvor store frekvenserne var, det fandt grækerne ikke ud af. I slutningen af 16-tallet blev det almindeligt at dele en oktav i 12 lige store dele på den måde, at forholdet mellem frekvenserne af en tone og den foregående er 1,059, nemlig den tolvte rod af 2. På Sauveurs tid var forholdet mellem frekvenserne af to tilfældige toner i den anvendte toneskala altså kendt.

totoner.mp3

Det var ikke meget, man vidste om lyd, før Sauveurs undersøgelser. Men lydens hastighed kendte man. Det er ikke svært at få en fornuftig ide, om hvor stor lydens hastighed er. Hvis man står et sted, hvor der er ekko, kan der f.eks. gå ca 2 sekunder fra råbet til man hører ekkoet. Hvis der så er 300 meter hen til den væg, der danner ekkoet, så har lyden gået 600 meter på de to sekunder, altså 300 meter pr. sekund. Jeg kan også huske, at jeg engang som dreng stod på en mark og så på en landmand, der på nabomarken slog på en maskine med en hammer. Og så nåede lyden først hen til mig, når landmanden havde hævet hammeren til næste slag. Det vil jo også kunne give en bestemmelse af lydhastigheden.

En tidlig mere omhyggelig måling af lydens hastighed blev udført af Rømer, Picard og Cassini omkring 1680. De målte tiden mellem glimtet og braget fra en kanon. Resultatet var, at lyden var 7 sekunder om at bevæge sig de 7680 pariserfod, der var hen til kanonen. Da en pariserfod er 32 cm, giver det en lydhastighed på 350 m/s. Et fornuftigt resultat, da det moderne tal er 340 m/sek.

En anden ting, der skal ligge klart, før man kan forstå Sauveurs frekvensbestemmelse, er det såkaldte superpositionsprincip, som gælder for mange typer af bølgebevægelser. Princippet siger, at to bølgebevægelser, der samtidig findes i et medium, kan foregå, uden at de påvirker hinanden. Princippet gælder for lysbølger og lydbølger. Det viser sig f.eks. ved, at en gul og en blå lysstråle kan krydse hinanden uden at farverne blandes. Og man kan jo også godt snakke i munden på hinanden, uden at det man siger, bliver forvrænget hos tilhørerne.

På billedet til venstre illustrerer vi superpositionsprincippet med et billede af vandbølger. Der er to samtidige bølgebevægelser: Der er nogle store bølger med en bølgelængde på et par meter, og der er nogle små, hvis bølgelængde er ca 20 cm. De to typer af bølger påvirker ikke hinanden. Superpositionprincippet siger, at de små bølgers bølgetoppe bliver lagt til de store bølgers overflade, og de små bølgers bølgedale bliver trukket fra de store bølgers overflade.

Den fænomen, der førte Sauveur frem til bestemmelse af en lydbølges frekvens, var velkendt af orgelbyggere. Det viste sig, når man samtidig spillede to dybe toner, der ligger tæt på hinanden, som f.eks. et c og et cis. Så kunne organisten tydeligt høre, at begge toner var der, men den samlede tonestyrke varierede langsomt, i et øjeblik var lyden stærk og et øjeblik senere var den svagere. Fænomenet gentog sig periodisk. Sauveur fandt forklaringen.

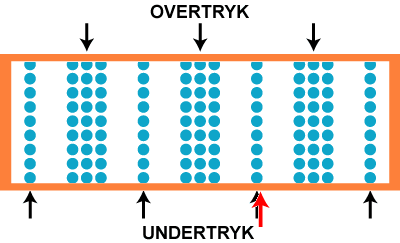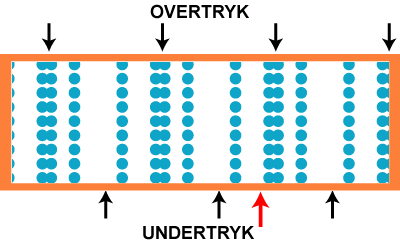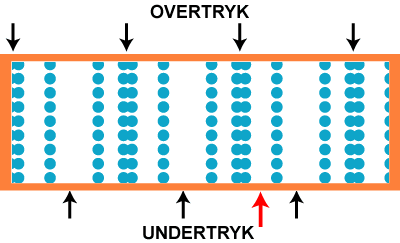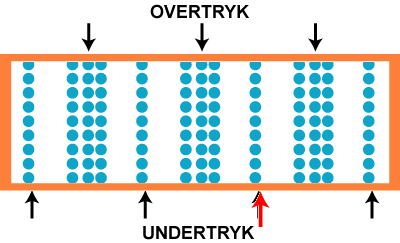På figuren til venstre viser vi 144 luftpartiler. De ligger stille og roligt, og luftens tryk er konstant. Så bliver der sat gang i en lydgiver ude til højre, det kan f.eks. være en orgelpibe, der spiller et dybt c. Det er en ren tone, dvs. en tone med én bestemt frekvens. Så begynder hver enkelt luftpartikel at svinge frem og tilbage, sådan som det er vist på animationen til højre. Lydens frekvens er antallet af svingninger pr. sekund. At det er en ren tone betyder, at svingningerne er sinusformede.

Hvis vi nu stiller os på et bestemt sted, f.eks. der hvor den røde pil peger, oplever vi skiftende overtryk og undertryk. Trykvariationen i tidens løb kan beskrives med en kurve som den øverste på figuren nedenfor. Vi har vist 21 perioder af svingningen. Vi kalder frekvensen f.

Hvis vi dernæst beder organisten om at spille en lidt højere tone, cis, får vi en trykkurve, der ser lidt anderledes ud. Denne gang er der i samme tidsinterval plads til 23 perioder. Den nye trykkurve er vist i midten på figuren nedenfor. Vi kalder dens frekvens for g.

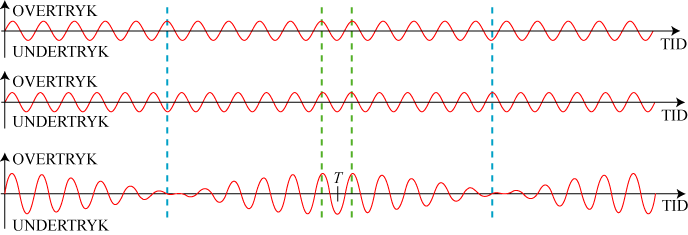
Så beder vi organisten spille begge de to toner samtidig. Så får vi en ny trykkurve. Ifølge superpositionsprincippet kan vi regne det nye tryk til et bestemt tidspunkt ud ved at addere de to tryk på kurverne ovenfor til samme tidspunkt. Det har jeg så gjort til ethvert tidspunkt, og derved fremkommer den resulterende trykkurve, som er vist nederst. Det mærkelige udseende er måske lidt overraskende, men ved lidt eftertanke forstår man det: Lige til at begynde med er de to øverste kurver næsten ens. Derfor får man ved additionen en kurve, der har dobbelt så store udsving. Men efterhånden som tiden går, kommer de to øverste svingninger ud af takt, og når man kommer hen i nærheden af den første punkterede blå linie er svingningerne næsten modsatte, og ved additionen får man derfor en kurve meget tæt på aksen. Når man så kommer hen til de grønne punkterede linier, er svingningerne kommet i takt igen, og vi får igen store udsving forneden.

Det, som vi har forklaret her, er Sauveurs forklaring på organisternes iagttagelse af den varierende tonestyrke. (- Det er egentlig ulogisk, at det hedder iagttagelse, også når det foregår gennem øret.) Det var i første omgang en kvalitativ forklaring, men Sauveur gjorde det til en kvantitativ. Som nævnt ovenfor er g = 1,059f. Svingningstiden for den langsomt varierende tonestyrke er markeret T på den nederste kurve. På T sekunder er der præcis én svingning mere i cis-et end i c-et. I T sekunder er der Tf svingninger for oven og Tg svingninger i midten. Derfor er Tg = Tf +1. Heraf fås ved division med T at 0,059f = 1/T. Den søgte frekvens f er altså f = 1/(0,059·T). Ved anvendelse af dybe toner bliver T så stor, at den umiddelbart kan måles. Hvis f.eks. T = ½ sek bliver f = 35 Hz, en tone som er hørbar. Når man først har fundet én frekvens er det som nævnt let at udregne frekvenserne for alle de andre toner i vores toneskala.

Når man kender hastigheden og frekvensen for en bølgebevægelse, kan man regne bølgelængden ud. Den er forholdet mellem hastighed og frekvens. F.eks. har kammertonen (et a ca. midt på klaveret) frekvensen 440 sek^-1. Da lydens hastighed er 340 m/sek bliver bølgelængden for kammertonen 0,77 meter. Hvis animationen ovenfor viser kammertonen, er der altså 77 cm mellem de sorte pile.

Forestil dig, at du før Sauveur havde sagt til en fysiker: "Det er godt at vide, at frekvensen for en tone er dobbelt så stor som for oktaven under. Men det ville sige mig mere, hvis jeg kunne få at vide, hvor store frekvenserne faktisk er. Kan du ikke finde ud af det?" "Håbløst," ville han svare, "hvordan skulle man kunne tælle svingningerne af noget, der svinger så hurtigt som strengene på et musikinstrument?" Så ville du nok holde din mund, men det gjorde Sauveur ikke. Han fandt frekvenserne ved at udnytte et kendt fænomen, der svingede så langsomt, at frekvensen kunne måles. Det var virkelig smart gjort!

Hvis du støder på et ord, hvis betydning du ikke kender, så søg på ordet.