|
Forside
Søgning
Liste |  |
Mere om d´Alemberts artikel om tandhjul i Encyclopedien
Indledende bemærkninger
I Encyclopedien har D´Alembert en række artikler om formen på tænderne af et tandhjul. Her beskriver vi den artikel, der står under horologi under opslagsordent "dent" dvs. tand. Jeg anbefaler, at man sætter sig ind i artiklen om Rømers tænder inden man går i gang med denne side. Hovedindholdet er en beskrivelse af en tandform, der sikrer, at når det ene af to tandhjul i indgreb drejer sig med konstant vinkelhastighed, så vil det andet også dreje sig med konstant vinkelhastighed. De tandhjul, som Rømer beskrev, kalder vi her for "rømerske".
I vores kommentarer her kalder vi to tandhjul i indgreb for "jævne", hvis det ene drejer sig med konstant vinkelhastighed, når det andet gør det. De rømerske tandhjul er én (blandt mange) former for jævne tandhjul.
| 0 | Artiklen Inddelingen i numre er forfatternes Oversættelse af Maia Nielsen | Kommentarer | ||
| 1 | Tand bruges også inden for Mekanik, om de små udstående dele omkring et hjul, som kommer i forbindelse med tænderne i et mindre tandhjul for at få det i omløb. | I hele artiklen er det et stort tandhjul, der driver et mindre | ||
| 2 | Hjultændernes udformning er af stor betydning, og man bør give den meget omhu, når man bygger en maskine. | . | ||
| 3 | Man kan have beregnet med stor nøjagtighed forholdet mellem to tandhjul, og dermed hvilket moment en maskine kan gives med en bestemt kraft; | 1.sætning betyder forholdet mellem antallene af tænder. 2. sætning må handle om forholdet mellem de momenter, som tandhjulene påvirker hinanden med. Der skelnes åbenbart ikke mellem kraft og moment. | ||
| 4 | men hvis det større hjuls tænder, og det mindre hjuls tænder, som de påvirker, ikke er udformet sådan, at det mindre hjul gives en ensartet bevægelse, hvilket vil sige at den kraft det større hjul skal udøve for at få det mindre hjul i omløb ikke konstant er den samme, vil beregningen ikke sige noget om maskinens egentlige effektivitet. | Det er uklart hvad der menes med effektivitet, og der siges intet intet om et bremsende moment, der må virke udefra på det lille hjul. Hvis der ikke var sådan et moment, og hvis der ikke var gnidningsmodstand, ville jævne hjul kunne dreje i det uendelige uden ydre påvirkning, hvad enten de var rømerske eller ej. Hvis der er gnidning, og hvis der er et ydre moment er der et energitab som varme i begge tilfælde. | ||
| 5 | for da det større hjul sommetider skal udøve mere, sommetider mindre kraft, kan man ikke regne med mere end maskinens lavest mulige effektivitet; hvilken ofte er meget svær at kende. Dette viser hvor nødvendigt det er, at tændernes udforming er korrekt. |
| ||
| 6 | Ikke desto mindre, og til trods for at man i flere århundreder har bygget maskiner som bruger tandhjul, har Mekanikerne ganske overset disse aspekter, og overladt det til arbejdsmændene at udarbejde denne del af maskinerne, og disse havde ingen anden regel heri end at det større og det mindre tandhjuls tænder skulle være formet sådan at de frit kunne gribe ind i hinanden, og altså ikke var årsag til nogen standsning. | I 1675 benyttedes enkelte rømerske tandhjul i Rømers planetmaskiner og ure. | ||
| 7 | Hr. de la Hire, af det Kongelige Videnskabs Akademi, talte først om emnet. Han behandlede det i længden i sin traktat om epicykloider. | Rømers tandhjul blev beskrevet af Huygens i 1674. De la Hires bog om bl.a. epicykloider udkom i 1695. De la Hire fandt ikke andre tandformer end Rømers, men muligvis uafhængigt af Rømer. | ||
| 8 | Af de forkellige krumninger for tænder som han afgør for de forskellige typer mindre hjul er det dog kun den for de tænder som driver et såkaldt lanternehjul (formet som et bur eller en lanterne) som kan føres ud i livet. Hr Camus har udfyldt de mangler som fandtes i Hr de la Hires traktat. |
Den indledende påstand er forkert. Det virker ikke som om D´Alembert har forstået meningen med det hele. | ||
| 9 | Denne lærde matematiker afgør i sit "memoire af år 1733" hvilke kurver tænder bør have på det store og det mindre hjul for at det sidste drives ensartet af det første, enten ved at det større hjuls tand møder det mindre hjuls tand langs linje RI (fig 102, plan XIX. Urværk) som kaldes centerlinjen; |
Tandhjulene på figuren kan ikke dreje, og kurveformen er ikke angivet. | ||
| 10 | eller ved at de mødes (fig. 99) før denne linje og forbliver i forbindelse efter den; |
Rotationsretning og tandform er ikke beskrevet. Det lille tandhjul ligner et rømersk tandhjul, specielt derved at de retlinede dele af tænderne peger mod hjulets centrum. I artiklen er der 7 illustrationer af tandhjul i inndgreb. Illustrationen her er den eneste fornuftige. De andre er enten umulige eller uhensigsmæssige | ||
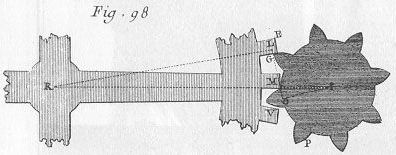
| 11 | eller endelig ved at (fig 98) tanden på det større hjul møder tanden på det mindre hjul før centerlinjen og driver det mindre hjul op til denne linje: man kan sige at han herved at gjort Urværk en meget stor tjeneste. |
Opdelingen i de to tilfælde 10 og 11 er meningsløs. Det er uhensigtsmæssigt, at det lille hjul på figuren her kan dreje sig lidt frem og tilbage , uden at det store flytter sig. | ||
| 12 | For omend dygtige urmagere måtte have ganske rigtige ideer om emnet, forblev den korrekte udformning af hjultænderne en slags problem for dem. | Påstanden er korrekt. | ||
| 13 | Helst ville vi her indsætte samme værk, som vi erkender at have draget mange oplysninger fra; men da det er lidt for langt, og desuden demonstreret på en lidt for abstrakt måde for de fleste urmagere, vil vi forsøge at afhjælpe det ved at demonstrere ad anden vej, det som angår udformningen af tænderne på det større og det mindre hjul. | Hm, det gjorde det vist ikke lettere. | ||
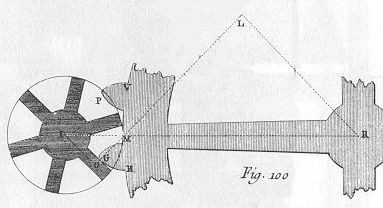
| 14 | Hvis vi forestiller os et hjul REV (fig. 98 og 100) og et mindre hjul PIG siger jeg at, hvis det større hjul skal give det mindre en ensartet bevægelse skal, i enhver situation som tænderne på det ene og det andet hjul kan befinde sig i under omløbet, de linjer som ligger vinkelret til tændernes flader, på det punkt hvor de kommer i berøring, alle mødes og gå igennem et punkt M på centerlinjen, og dette punkt skal være sådan placeret på linjen at RM står i samme forhold til MI som antallet af tænder på det store hjul til antallet af tænder på det mindre. |
Det fremgår af linje 28, at D´Alembert planlægger at bevise, at når alle de nævnte normaler går gennem M, så er tandhjulene jævne. Påstanden er rigtig. Se et bevis her på hjemmesiden undet 1742: En sætning om jævne tandhjul. | ||
| 15 | For at demonstrere dette, lad os forestille os LO, som ligger vinkelret til fladen på det mindre hjuls tand på det punkt G hvor det berører tanden på det større hjul; og IO, RL, linjer som er lagt vinkelret til denne linje fra I og R, som er center henholdsvis for det mindre hjul og det større hjul: linjerne RL og IO vil være udtryk for henholdsvis RL : den momentarm med hvilken det større hjulet skubber til det mindre; OI, den momentarm med hvilken det mindre hjul bliver skubbet. |
Jeg forstår ikke argumentet. Og jeg har mistro til det, fordi påstanden er rent geometrisk. Den siger jo, at når en variabel linje går gennem et bestemt punkt er tandformen jævn. Der tages ikke hensyn til at de to tandhjul normalt vil røre hinanden mere end et sted. Hvis tandhjulene er jævne, og hvis det lille tandhjul ikke er påvirket af andre momenter end det fra det store, er dette 0. Og hvis der er andre momenter, må de indgå i argumentationen. "Beviset" fylder frem til 27. Påstanden er rigtig. Se et bevis her på hjemmesiden undet 1742: En sætning om jævne tandhjul. | ||
| 16 | Det vil forekomme åbenlyst, hvis man noterer at RL´s momentarm ligger vinkelret til OI linjen og dermed at de uendeligt små buer som i øjeblikket dannes af punkter L og O vil have den samme længde: som sker, når en momentarm har en øjeblikkelig virkning på en anden som ligger vinkelret. | . | ||
| 17 | RL er altså udtryk for det moment med hvilket det større hjul skubber det mindre, og IO for det med hvilket det mindre hjul skubbes; det er klart at hvis den momentarm som det mindre hjul skubbes af altid står i det samme forhold til den momentarm som det større hjul skubber den med vil det større hjul altid, på ethvert punkt i føringen, måtte udøve en ensartet kraft for at holde det mindre hjul i omløb. | Nej, der skal ingen kraft til at holde det lille hjul i omløb. Hvis tandhjulene ikke er jævne og hvis man tager hensyn til deres masser skal der et hurtigt varierende moment til, og det skal så indgå i argumentationen. | ||
| 18 | da værdien, målt i grader, for hver af de buer som dannes, i samme øjeblik, af momenterne RL og OI står i modsat forhold til deres længde, eller i samme forhold som OI til RL; står værdierne, målt i grader, af de buer som dannes af det større og det mindre hjul på et og samme øjeblik igen i samme forhold som OI & RL: | |||
| 19 | Men da de momentarme som svarer til IO og RL altid står i samme forhold, på alle punkter i omløbet, må værdien i grader af de buer som dannes i samme øjeblik af det større og det mindre hjul ligeledes være den samme. Og vinkelhastighederne for det mindre og det større hjul svarer til disse buer. | |||
| 20 | Herudover er det kendt, via Mekanikkens principper, at for at to kræfter skal være i balance skal de stå i omvendt forhold til deres hastighed. Derfor vil to konstante kræfter som i modsat retning påvirker henholdsvis det større og det mindre hjul, og som kommer i balance på et hvilket som helst punkt af omløbet, stå i forhold til det mindre og det større hjuls vinkelhastigheder på dette punkt: men da disse hastigheder på alle punkter af omløbet står i det samme forhold vil krafterne altid være i balance; derfor er den kraft, hvormed det større hjul driver det mindre på alle punkter den samme; altså drives det mindre hjul ensartet. | Jeg ved ikke hvilket mekanisk princip, der hentydes til. | ||
| 21 | Dette Mekanikkens princip værende fastslået, lad os nu forestille os at tanden på det større hjul (se fig. 98 og 100) befinder sig i en hvilkensomhelst E G situation, og at den vinkelrette linje fra punkt G går igennem et punkt M som ligger på centerlinjen ; RL er, som set heroverfor, udtryk for den momentarm, hvormed det større hjul skubber til det mindre, og OI for den momentarm, hvormed det mindre hjul bliver skubbet. |
Der skal som nævnt ikke noget moment til at vedligeholde det lille tandhjuls rotation. | ||
| 22 | Lad os ligeledes formode, at tanden på det større hjul og tanden på det mindre hjul befinder sig på centerlinjen og dermed kommer i berøring på dette samme punkt M, RM er nu den momentarm med hvilken det det større hjul skubber til det mindre, & MI er momentarmen med hvilken det mindre hjul bliver skubbet. | |||
| 23 | Men på grund af ligheden mellem trekanterne RLM, MOI, har vi nu RL:OI::RM:MI; i henhold til princippet ovenover vil det større hjul altså føre det mindre ensartet på de to punkter M og G, siden forholdet mellem momentarmene RM og MI på punkt M er det samme som forholdet mellem momentarmene RL og OI på punkt O. | |||
| 24 | Det samme kan demonstreres på samtlige andre punkter i omløbet, sålænge vinkelrette linjer til tandfladen på både det større og det mindre hjul går igennem samme punkt M. Ydermere skal det større og det mindre hjuls vinkelhastigheder stå i omvendt forhold til deres antal tænder da det større hjul skal drive det mindre ensartet, bør deres forskellige vinkelhastigheder på ethvert punkt i omløbet stå i det selvsamme forhold. | |||
| 25 | Er disse antal tænder givet, er det mindre og det større hjuls vinkelhastigheder det derfor ligeledes. Og da det mindre hjuls vinkelhastighed på punkt M står i samme forhold til det større hjuls på samme punkt, som momentarm MR til momentarm MI ; skal MR stå i samme forhold til MI som antallet af tænder på det større hjul til antallet af tænder på det mindre hjul. | |||
| 26 | Ellers stod det mindre hjuls vinkelhastighed på dette punkt ikke i samme forhold til det større hjuls som det større hjuls tandtal til det mindres hjuls. Derfor må punkt M skære linje RI således, at RM står i samme forhold til MI som det større hjuls antal tænder til det mindres hjuls. | |||
| 27 | For at et større hjul kan drive et mindre hjul ensartet kræver det altså at linjer som ligger vinkelret til tandfladen på det større hjul og til tandfladen på det mindre hjul på alle punkter i omløbet falder sammen med en linje som går igennem et punkt M, som skærer centerlinjen således at RM står i samme forhold til MI som antallet af tænder på det større hjul til antallet af tænder på det mindre. QED. | Her er det uklart, hvad der er givet, og hvad der skal bevises. Beviset slutter her. Det kan godt være, at det er rigtigt nok, men jeg har ikke forstået det. | ||
| 28 | Denne demonstration dækker tydeligvis de tre muligheder, for tanden på det større hjul kan befinde sig i enhver situation i omløbet - altså både op til eller efter centerlinjen. Det står nu klart at hvadenten tanden på det større hjul møder tanden på det mindre hjul netop på centerlinjen, eller de mødes i opløbet til denne linje og skilles netop på den, eller de mødes inden centerlinjen og skilles efter denne; vil det mindre hjul bliver drevet ensartet hvis de linjer som står i en ret vinkel til punkterne hvor tænderne på det større og det mindre hjul kommer i berøring, i enhver situation under omløbet, går igennem et bestemt punkt M som ligger på centerlinjen og er således placeret på denne, at RM står i samme forhold til MI som antallet af tænder på det større hjul til antallet af tænder på det mindre hjul. | Først her bliver det klart, hvad D´Alembert mener at have bevist: Betragt to tandhjul i indgreb. Ved en normal forstås en linje gennem et røringspunkt mellem to tænder, som er vinkelret på den fælles tangent til de to tænder i røringspunktet. Så siger D´Alembert, at når alle normaler går gennen M, så er tandhjulene jævne. Påstanden er rigtig. Se et bevis her på hjemmesiden undet 1742: En sætning om jævne tandhjul. | ||
| 29 | Ydermere gælder denne demonstration for mange forskellige typer drivværk hvor det er ønskeligt at det større hjul driver det mindre hjul ensartet, hvordan end tænderne på de to hjul måtte være udformet. | Ja, hvis ellers alle de nævnte normaler går gennem M. | ||
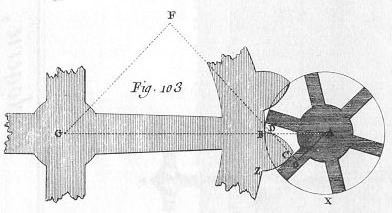
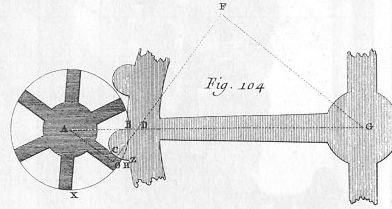
| 30 | Det følger af demonstrationen overfor, (se fig. 103 og 104) at hvis en vinkelret linje til tanden på det større hjul på et bestemt punkt C hvori den kommer i berøring med tanden på det mindre hjul, ikke går igennem punkt M men igennem punkt F, placeret imellem R og M; da vil tanden på det større hjul udøve mere kraft for at drive det mindre hjul på dette punkt C end da de to tænder befandt sig på centerlinjen og kom i berøring på punkt M; |
Argumentationen er fornuftig, men fra et matematisk synspunkt indeholder den irrelevante begreber som kraft og moment. | ||
| 31 | og hvis samme retvinklede linje tværtimod går igennem et punkt T placeret imellem M og I vil denne kraft være mindre; det giver sig selv, siden det mindre hjul i det første fald vil dreje langsommere, vinkelhastigheden i forhold til det større hjul værende, som vi har vist det, i samme forhold som RF til FI; og i det andet fald vil det mindre hjul dreje hurtigere, da dens vinkelhastighed står i samme forhold til det større hjul som RT til TI. | |||
| 32 | Alt dette kunne have været demonstreret på kortere og mere geometrisk vis, men vores bedste overbevisning var at alt måtte vige for klarheden og nødvendigheden af at gøre os forståelige for fagfolk. Da vi nu har set hvilke betingelser skal opfyldes i et tandhjulsdrev for at det større hjul skal drive det mindre hjul ensartet; vil vi her videre demonstrere at når det større hjul møder det mindre på eller efter centerlinjen kræver det, for at opnå samme effekt, at tandfladen på det mindre hjul er en lige linje som peger mod centrum, at tandfladen på det større hjul er et segment af en epicykloide draget af et punkt på en cirkel hvis diameter er det mindre hjuls radius, som er i omløb udenom det større hjuls omkreds. | d´Alembert hævder her, at hvis et par tandhjul er jævne, da vil et lille hjul have tænder med retlinede sider, der peger ind mod hjulets sider. Denne
påstand er forkert, se et modeksempel her, som er hentet fra vores side om Rømers tandhjul.
| ||
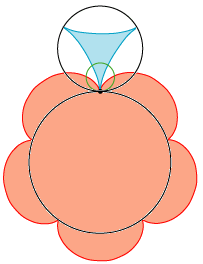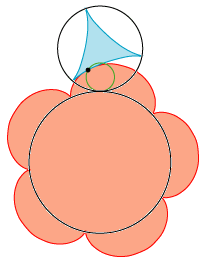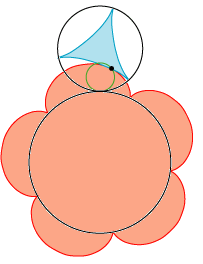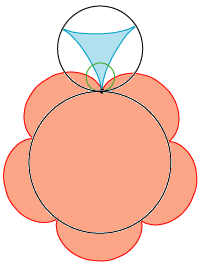
| 33 | Hvis en cirkel COQ (fig. 97 n° 2) er i omløb uden om omkredsen på en anden cirkel ALE, eller indenfor denne, som i M, vil ethvert punkt C på den første cirkel danne, i sin bevægelse, en linje af den type som kaldes epicykloide. Se epicykloide. | 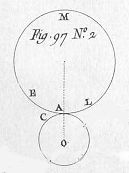 Det er Rømers ide at bruge epicykloider i tandhjul. Det er Rømers ide at bruge epicykloider i tandhjul.
| ||
| 34 | Hvis cirkel COQ har en anden cirkel ALEs radius til diameter, vil den da, i dens kurs inden-for denne cirkels omkreds, som ved M, tegne en lige linje som er diameter til denne cirkel ALE. Se epicykloide. Med det in mente, lad os antage cirklerne PIG og RVE (fig 95. nr 2) som henholdsvis forestiller det mindre og det større hjul, og hvis diametre HI og HR står i samme forhold til hinanden som deres antal tænder: lad os forestille os to små cirkler COQ hvis diameter er det mindre hjuls radius & som ligger så præcist over hinanden at de falder sammen; | 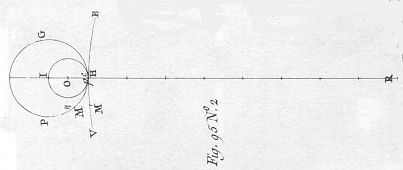 | ||
| 35 | centrum for dem ligger præcist i det samme punkt O på centerlinjen og punkt C i H eller D på samme linje: lad os nu tænke (fig. 94 nr 4) at det større og det mindre tandhjul er i omløb om deres centrer, fra M til X, og at disse to små cirkler også er i omløb, det ene indenfor det mindre tandhjuls omkreds, det andet udenom det større tandhjuls omkreds, på en sådan måde at hver bue som gennemgås af det større og det mindre tandhjul i den ene retning gennemgås af disse to små hjul ligeledes i modsat retning; | 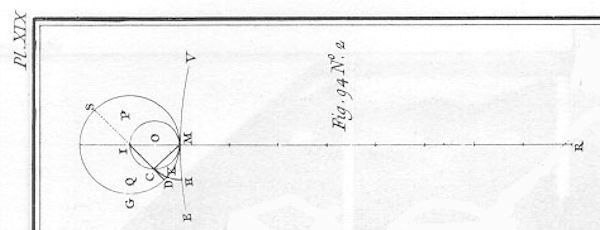 | ||
| 36 | sådan at når det store og mindre hjul har bevæget sig, det ene i buen M H, det andet i buen M D, har de to COQ cirkler også dækket, men i modsat retning, det ene udenom det store hjul og det andet indeni det mindre, den samme bue, MC, som er lig med buen MH eller MD. | |||
| 37 | Denne bevægelse af de to COQ cirkler vil forårsage, at deres center O ikke vil forlade centerlinjen R I, dersom hver gang de forsøges drevet bort fra denne centerlinje af det større og det mindre tandhjuls bevægelse langs en hvilken som helst bue vil de føres tilbage til den, ved at de triller tilbage, i modsat retning, ad en bue af samme længde. | |||
| 38 | Lad os nu forestille os et øjeblik at det større hjul, i sin bevægelse fra M til H, driver det mindre hjul udelukkende ved at gnide imod den, vil effekten dog være den samme; det mindre hjul vil blive drevet ensartet, da man vil kunne se dens forhold til det større hjul som to ruller hvoraf den ene får den anden i omløb simpelthen ved at de kommer i berøring. Men de små cirkler i bevægelse, det ene indeni det lille hjul, det andet uden om det store hjul, vil være i samme situation som cirklerne COQ, M (fig. 96, nr 2) & COQ som trillede henholdsvis indenfor ALE's omkreds og udenom den. | |||
| 39 | Således vil punkt C i cirkel COQ, som ruller indenfor det mindre hjul bevæge sig langs en ligne linje DS, som er diameter for det mindre hjul, og en del af hvilken, kaldt CD, vil svare til en anden bue, CM, som denne cirkel på samme tid gennemgår. Ligeledes vil punkt C på cirklen COQ som triller udenom det større hjuls omkreds danne en epicykloide en del af hvilken, CH, på samme måde svarer til buen MH, som er lig med CM. | |||
| 40 | Men da disse to cirkler har samme diameter og og altid i samme retning danner buer af samme længde, på grund af det større og det mindre hjuls ensartede bevægelse, vil det punkt som udgør C i den cirkel som triller indenfor det mindre hjul stå på samme sted som det punkt som udgør C i den cirkel som triller udenom det store hjul. Dermed vil punkt C, på DI segmentet af den lige linje DS og punkt C på epicykloid CH være beskrevet på en gang. | |||
| 41 | Og i en hvilken som helst situation af det punkt som udgør C vil linjen MC, som går igennem punkt M på centerlinjen, altid være vinkelret til linjen CD, eller ID, da disse to linjer altid vil danne en vinkel hvis spids vil ligge på cirklen COQs omkreds og hvile på dens diameter. Ligeledes vil linjen MC også ligge vinkelret til den uendeligt lille del af epicykloiden CK som på samme tid beskrives, da MC vil være som den radius, som drager CK, en uendeligt lille cirkelportion. | |||
| 42 | Hvis altså det mindre hjuls tandflade, så vel som det større hjuls tandflade, er dannet ved at følge et punkt på en cirkel hvis diameter er lig med det mindre hjuls radius og som bevæger sig indenom dens omkreds og udenom det større hjuls omkreds, vil de derved have samme egenskaber som linjerne CS og CH, og derfor, i alle situationer de måtte befinde sig i, vil de linjer som ligger vinkelret til de punkter hvor de to tænder kommer i berøring falde sammen alle gå igennem samme punkt M. | |||
| 43 | Men dette punkt M vil, per konstruktion, skære centerlinjen efter samme forhold som antallet af tænder på henholdsvis det mindre og det større hjul. Altså, hvis det mindre hjuls tandflade dannes af en lige linje som peger mod center, og det større hjuls tandflade dannes af en epicykloide draget af en cirkel hvis diameter er det mindre hjuls radius og som triller udenom det større hjuls omkreds, vil det større hjul drive det mindre hjul ensartet, siden de linjer som ligger vinkelret til det mindre hjuls og det større hjuls tænders flader på alle punkter hvor de kommer i berøring falder sammen, og altid må gå igennem et punkt M på centerlinjen, som skærer denne linje i henhold til de opstillede betingelser. | |||
| 44 | Det er let at se at den samme demonstration gælder for andre typer epicykloider, hvilket vil sige at et større hjul altid vil drive et mindre hjul ensartet, hvis det mindre hjuls tænders flader er segmenter af epicykloider draget af et punkt af en cirkel som triller indenfor det mindre hjul, og det større hjuls tænder har flader udformet efter andre epicykloider, draget af samme cirkel i omløb udenom det større hjuls omkreds. Da den kraft som det større hjul udøver for at få det mindre hjul i omløb altid er ensartet, er det omvendt indlysende at den kraft hvormed det mindre hjul påvirker det større ligeledes er det. | D´Alembert skriver her om en epicykloide, der beskrives af et punkt på en cirkel, der ruller inden i en anden cirkel. Sådan en kurve vil vi i dag kalde en hypocykloide. | ||
| 45 | For hvis det mindre hjuls kraft på et hvilket som helst punkt i omløbet var en anden end på et andet punkt ville det større hjuls modvirkende kraft også være det: altså ville denne kraft ikke altid være ensartet; hvilket er selvmodsigende. I det tilfælde hvor PIG, det mindre hjul, driver REV, det større hjul (fig. 102) er det indlysende, at det mindre hjuls tand vil møde det større hjuls tand før centerlinjen, og drive den op til denne; heraf er det nemt at udlede at et stort hjul hvis tand møder et mindre hjuls tand inden centerlinjen og driver den dertil, befinder sig præcis i samme situation. | 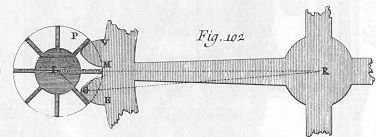 | ||
| 46 | Men vi har set at det mindre hjul driver det større ensartet sålænge det større hjuls tænder har flader som linjer, der peger mod centrum, og det mindre hjuls tænder har flader som segmenter af en epicykloide tegnet af en cirkel hvis diameter er det mindre hjuls radius og som er i omløb på det større hjuls omkreds. Altså kræver det, for i dette tilfælde at opnå en ensartet bevægelse, at det større hjuls tænder har flader som lige linjer, der peger mod centrum, og at det mindre hjuls tænder har flader som segmenter af en epicykloide tegnet af en cirkel med diameter som det større hjuls radius,og som er i omløb udenom det mindre hjuls omkreds. | |||
| 47 | Ligeledes igen når (som i fig. 99) tanden på det større hjuls driver tanden på det mindre hjuls både op til og efter centerlinjen, skal den være udformet efter to linjer, den ene, GK, en lige linje som peger mod det store hjuls centrum, skal drive det mindre hjul op til centerlinjen, og den anden, GE, en kurve som driver det derefter; og det mindre hjuls tand skal være udformet efter to andre linjer, den første en kurve, GS, hvormed tanden på det større hjuls driver det mindre hjul op til centerlinjen, og den anden en lige linje DG, som peger mod det mindre hjuls centrum og med hvilken tanden på det større hjuls driver det mindre hjul efter centerlinjen. Kurven på det større hjuls tænder skal have form efter en epicykloide tegnet af en cirkel hvis diameter er det mindre hjuls radius, og som er i omløb udenom det større hjul; kurven på det mindre hjul skal være en epicykloide draget af en cirkel hvis diameter er radius på det større hjul, og som er i omløb udenom det mindre hjul. | 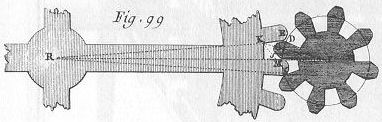  Det lille tandhjul her minder meget om et af Rømers tandhjul, som dels er beskrevet af Huygens, og som Rømer også fik fremstillet, formodentlig af den berømte franske instrumentmager Thuret. Nedenfor viser vi en af de tegninger af Rømers tandhjul, som Huygens lavede. | ||
| 48 | Vi har lige vist hvilke kurver det større og det mindre hjuls tænder skal følge, i de tre forskellige situationer som de kan mødes i; det er ikke længere nødvendigt at spekulere på hvilket af de tre tilfælde er mest fordelagtigt. Det er indlysende at det er tilfældet hvor tanden på det større hjul møder tanden på det mindre hjul netop på centerlinjen; fordi 1. det minimerer gnidningen af de to tænder mod hinanden, da de ikke stemmer mod hinanden som de gør i de to andre tilfælde, og 2. fordi snavs, i stedet for at blive fejet indad som i de to andre tilfælde, bliver fejet udad. | |||
| 49 | Kun i en omstændighed bør man foretrække at forbindelse dannes før og varer til efter centerlinjen; nemlig når det mindre hjul har et for lille tandtal, som 6, 7 osv op til 10, udelukkende; det skyldes at hvis det mindre hjul har så få tænder, og hvis tænderne på de to hjul først mødes på centerlinjen, kan de slet ikke gribe ind i hinanden, som det er nemt at udlede af at afstanden mellem toppen af det større hjuls tænder er større end afstanden mellem toppen af det mindre hjuls tænder på samme punkt. Vil man bekræfte dette ved en beregning, vil man notere at i trianglen RIG (fig 102) hvor af man kender to to sider og vinklen ligeledes, er det nemt at kende den tredje, som vil give omsætningsforholdet, og så vel som vinklen IRG, som for at tænderne skal kunne gå i greb bør være mindst 2 grader mindre end halvdelen af vinklen mellem toppen af to nabotænder. |  | ||
| 50 | Med hensyn til den kurve som det større hjuls tænder bør have for at kunne drive et mindre hjul som ligger i et andet plan, som for eksempel i et kronhjul, bør den være et segment af en cykloide; og forestiller vi os at fladen på det mindre hjuls tand er en lige linje pegende mod centrum bør denne cykloide være draget af en cirkel hvis diameter er det mindre hjuls radius. Forklaringen på dette vil være indlysende, blot man har forstået overstående. | |||
| 51 | Der ville være meget mere at sige om dette emne, som er blevet ganske overset og som dog spreder sig meget længere end man almindeligt forestiller sig; men det ville gøre nærværende artikel endnu længere, end den allerede er. Man vil finde under artiklen Lanternehjul alt hvad angår udformningen af tænder på større hjul som skal i greb med denne type mindre hjul. Se ligeledes Drev, Hjul, Pignon, Lanterne, Aile (tand på mindre hjul), Menee (føring), Epicykloide, Cykloide, osv. | Til slut må jeg sige, at jeg er skuffet over indholdet af denne artikel af
D´Alembert i Den Store Franske Encyclopedi. Indholdet kan sammenfattes til to ting:
1. Via de la Hire har D´Alembert fået kendskab til rømerske tandhjul, men man får ikke indtryk af, at han har forstået den grundlæggende ide. Der er ingen figur med tandformer forskellige fra Rømers. specielt har D´Alembert ikke kendskab til Eulers tandhjul. 2.Den eneste nyhed i artiklen er sætningen om hvornår tandhjul er jævne, den sætning vi beviser her på hjemmesiden under 1742: En sætning om jævne tandhjul. Jeg ved ikke hvem der først har bevist denne sætning. D´Alemberts bevis er utilfredsstillende. |
| Hvis du støder på et ord, hvis betydning du ikke kender, så søg på ordet. |