Amperes formel

Den 21. juli 1820 sendte Ørsted en udførlig beskrivelse af sin opdagelse af at der er et magnetfelt i omegnen af en ledning, som der går en strøm i. Det medførte en voldsom aktivitet blandt europæiske fysikere. Omkring den 1. oktober opdagede den franske fysiker André-Marie Ampére blandt andet at to lange parallelle strømførende ledninger tiltrækker eller frastøder hinanden, afhængigt af strømretningerne. Disse forhold beskriver vi i vores artikel om Ampéres tidlige arbejder, der er link for oven. I den følgende tid arbejdede Ampere med et magnetfelt som skabes af to korte strømførende ledninger.

På billedet nedenfor har jeg tegnet et vandret rødt rektangel og et lodret grønt rektangel. Selve apparatet består i al sin enkelthed af to korte ledninger. Deres længder er ds og ds´.

Det er sådan, at d-et i længderne betyder at længderne er enormt små. F.eks er de så små, at man kan sige, at afstanden mellem de to ledninger er r, uden at man behøver at sige hvilke punkter på de to ledninger man måler afstanden mellem. Ved hjælp af ledninger, som ikke er vist, sendes der strømme af størrelsen i og í gennem ledningerne. Det er indrettet sådan at magnetfeltet fra de ikke viste ledninger ikke influerer på feltet i området mellem ledningerne. På billedet viser vi 6 af de 8 variable størrelser, som Ampere benyttede i den formel han fandt. Der er tale om i og í, der er strømstyrker, og ds og ds´, der er ledningslængder, og θ og θ´, der er vinkler. Ud over disse variable er der den nævnte afstand r mellem ds og ds´, og ω, der er vinklen mellem den blå trekant og den gule trekant.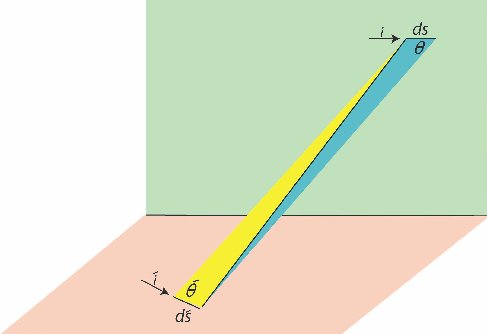

På Amperes tid havde man ikke enheder for strøm og spænding, og man kendte ikke begrebet modstand. Alligevel var det i nogle tilfælde muligt at finde ud af, hvor mange gange en elektrisk størrelse blev større eller mindre, når man foretog en eller anden ændring. For eksempel lykkedes det for Biot og Savart i oktober 1820 at bevise at feltstyrken omkring en lang lige ledning aftager med kvadratet på afstanden fra ledningen. Der er link til artiklen for oven.

Ampere sammenlignede sit arbejde om magnetfelter med Newtons arbejde med tyngdeloven, og han skrev følgende:

Jeg har helt igennem bygget på mine eksperimenter, og jeg har fundet den formel for for de kræfter, som bliver frembragt. Jeg har ikke søgt at finde nogen årsag til disse kræfter, idet jeg er overbevist om at al forskning af denne art må bygge på eksperimentel viden om lovene. Dernæst følger udledelse af retningen af disse kræfter, der virker i retning af en ret linje,der forbinder de to punkter langs hvilke kræfterne virker.

Den eksperimentelle baggrund for Amperes formel var fire ligevægtseksperimenter. Ampere beskriver principperne for sine eksperimenter således:

Principielt består eksperimenterne i at påvise, at en bevægelig ledning forbliver nøjagtigt i ligevægt når den er påvirket af lige store kræfter eller af lige store drejningsmomenter; kræfter og momenter som er skabt af faste ledninger af vilkårlig form og størrelse, uden at ligevægten bliver forstyrret under de givne betingelser. Herfra bestemtes ved beregning værdien af den indbyrdes påvirkning som to infinitisimale ledere skal påvirke hinanden med, uafhængigt af dimensioner, der er i overensstemmelse med forudsætningerne.

Baseret på disse eksperimenter udledte Ampere følgende formel

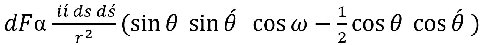
Formlen udtrykker en sammenhæng mellem alle de størrelser, som er beskrevet ovenfor og så den feltstyrkeændring dF, der sker når man ændrer på de nævnte størrelser. Efter dF står det græske bogstav α; det betyder ikke "lig med", men snarere noget i retning af "proportional med".

Jeg må indrømme, at jeg ikke forstår indholdet af formlen ovenfor. Hvis du er en læser, som forstår formlen, hører jeg meget gerne fra dig, se under forfattere på forsiden.

Hvis du støder på et ord, hvis betydning du ikke kender, så søg på ordet.