|
Forside
Søgning
Liste |  |
Archimedes (Arkimedes)
÷287 - ÷212

Archimedes var en græsk matematiker, fysiker, tekniker og opfinder. En anden stor matematiker, tyskeren Karl Friedrich Gauss (1777 - 1855) udtalte, at kun Isaac Newton kunne nå Archimedes´ niveau som matematiker.
Archimedes blev født i Syrakus, som ligger på Siciliens østkyst, men som dengang var græsk. Bortset fra studieophold i Alexandria, boede han i Syrakus det meste af sit liv. Hans far var astronom. I Alexandria blev han venner med bl.a. Eratosthenes, som han tilegnede et par af sine skrifter, bl.a. "Om Metoden". Eratosthenes blev senere leder af det store bibliotek i Alexandria. Archimedes blev dræbt hjemme i Syrakus under den anden puniske krig, hvor romerne, ledet af general Marcellus, erobrede Syrakus. Marcellus havde stor respekt for Archimedes og havde givet sine soldater ordre om at skåne ham; men det gik altså galt alligevel.
Archimedes adskilte sig fra de andre græske forskere: Han var både en stor "ren" matematiker og en stor "anvendt" matematiker. De andre græske matematikere nedlod sig ikke til andet end "ren" matematik og matematisk astronomi, måske fordi den græske overklasse havde slaver til det praktiske. Archimedes blev skaberen af den matematiske fysik og af mekanikken og hydrostatikken.
Teknik og opfindelser
Archimedes standsede ikke ved matematikken og fysikken; men han var også en stor tekniker og opfinder.
Han opfandt bl.a. "Archimedes´ skrue
eller snegl", et redskab til at løfte vand til bl.a. kunstvanding, som nedenfor vises i et billede og en animation:
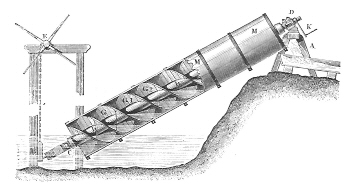
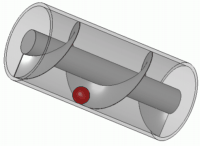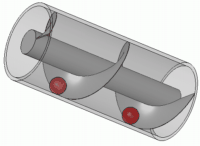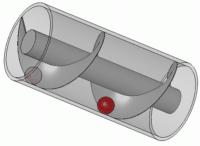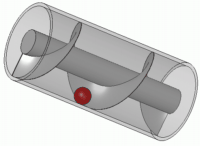
Archimedes opfandt (eller var én af opfinderne af) taljen, et instrument til at løfte tunge byrder, og hulspejlet. Historien om, at Archimedes konstruerede et enormt hulspejl, som skulle sætte fjendens, dvs romernes, skibe i brand, er dog kun en myte.
Han var også interesseret i skibe, nok p.gr.a. sin arbejdsgivers behov og ønsker, han var nemlig ansat hos kong Hieron 2. af Syrakus.
Én af Archimedes´ opfindelser er en slags planetarium eller himmelregnemaskine. Der er ikke bevaret nogen fysiske rester; men Cicero nævner, at general Marcellus, som erobrede Syrakus for romerne, hjembragte 2 eksemplarer af sådan et instrument. Det interessante er nu, at man i 1901 fandt et gammelt skibsvrag ud for den lille græske ø, Antikythera, som bl.a. rummede fragmenter af et lignende instrument, der blev dateret til perioden ÷150 - ÷100. Det var teknisk meget avanceret, og man har ikke andre fund af så avanceret teknik før ca. 1000 år senere. Se vores indførsel under ÷125 Antikythera.
Archimedes´ dilemma
På trods af Archimedes´ store bedrifter som praktiker, syntes han imidlertid selv, at de var lidt pinlige, - så præget af den græske, filosofiske ideologi var han alligevel. Archimedes´ dilemma belyser vi nedenfor i et citat fra Plutarch´s biografi om Archimedes. Plutarch (45 - 120) var en græsk-romersk filosof og forfatter af biografier om store græske og romerske personligheder.
"Archimedes besad en så ophøjet ånd, så dyb en sjæl og en sådan rigdom af videnskabelig forskertrang, at han - selv om han på grund af sine opfindelser havde vundet navn og ry for snarere at have en guddommelig end en menneskelig forstand - ikke ville nedlade sig til at efterlade sig et eneste skrift om sådanne emner. Han anså den mekaniske profession og enhver praktisk kunst for uværdig og vulgær og viede sig kun nidkært til sådanne emner, hvis elegance og dybsindighed ikke besværes af livets fornødenheder."
Citatet er gengivet fra Olaf Pedersen og Mogens Pihl: Historisk Indledning til den Klassiske Fysik.
Fysik
Inden for mekanik arbejdede Archimedes med tyngdepunkter og vægtstænger, og han grundlagde dermed statikken. Han arbejdede ikke med bevægelseslære (dynamik eller kinematik).
Archimedes´ første bog om definition af tyngdepunkter, som hed noget i retning af "Om Tyngdepunkter", er desværre ikke bevaret. Dog kan man få et indtryk af den hos Pappos, som arbejdede ca. 600 år senere end Archimedes.
I tobindsværket, "Om Plane Figurers Ligevægt og om Plane Figurers Tyngdepunkter", gennemgår Archimedes vægtstænger og tyngdepunktsbestemmelser.
Han grundlagde hydrostatikken i tobindsværket "Om Svømmende Legemer". Bl.a. fandt han "Archimedes´ lov", som siger følgende: "Når et legeme nedsænkes i væske, så taber det lige så meget i vægt, som den fortrængte væskemængde vejer".
Archimedes blev meget berømt på at løse en opgave, som hans protektor, kong Hieron 2. af Syrakus, stillede ham: Han skulle bestemme guldindholdet i kongens nye guldkrone, som kongen mistænkte for at være forfalsket ved iblanding af sølv. Archimedes løste opgaven uden at ødelægge kronen, ved at bestemme dens vægtfylde ved nedsænkning i vand, og så anvende sin "Archimedes´ lov". Konklusionen var, at kronen var forfalsket! Historien viser, at Archimedes kendte begrebet vægtfylde.
Matematik
Matematikerne Eudoxos (÷345) og Archimedes opfandt en form for integralregning. Archimedes brugte den bl.a. til at beregne arealer, begrænset af kurver, og arealer af krumme flader. De kaldte den "exhaustionsmetoden", og den beskriver en grænseovergang på en præcis måde. Ordet stammer fra arbejdet med "irrationale tal", dvs tal, der ikke kan skrives som hele tal eller brøker. Dem kunne grækerne ellers ikke lide og normalt heller ikke forholde sig til. De syntes ikke, at de var "rigtige tal". Archimedes kunne angive et irrationalt tal som grænsetallet for to talfølger, hvoraf den ene består af "rigtige tal", der alle er større end det undersøgte tal, mens den anden talfølge består af "rigtige tal", der alle er mindre end det undersøgte. Han talte så om, at det undersøgte tal blev fundet, eller "exhausted", af de to talfølger.
Archimedes bestemte arealet af en figur begrænset af krumme kurver ved at lave en lang række om- og indskrevne polygoner omkring den oprindelige figur, og så "gå til grænsen". Han benyttede bl.a. denne metode til at finde π med flere korrekte decimaler end tidligere bestemmelser, og hans værdi for π blev først forbedret flere århundreder senere. (π er forholdet mellem omkredsen af en cirkel og cirklens diameter. Det er et meget vigtigt tal i matematikken). Dette resultat for π skrev Archimedes om i "Om Målingen af Cirklen".
Det fortælles, at da Archimedes havde fundet formlen for kuglens overflade (4πR2), skrev han følgende til en fagfælle i Alexandria: "Jeg har fundet, at størrelsen af kuglens overflade er 4 storcirkler. - Sådan har det altid været; men jeg er den første, der har vidst det."
Archimedes´ "palimpsest"
Det er meget interessant at studere, hvordan Archimedes arbejdede som "anvendt" matematiker. Han skriver selv om det i et enestående værk, som den danske filolog og historiker Johan Ludvig Heiberg (1854-1928) (ikke forfatteren) genfandt i Konstantinopel i 1906: "Mekaniske Læresætningers Anvendelse", også kaldet "Om Metoden". Man havde ellers anset det for tabt.
Palimpsestets historie
Et palimpsest er et gammelt manuskript på pergament, hvor man senere har forsøgt at genbruge det dyre pergament ved at vaske og skrabe det, og dernæst skrive en ny tekst på det, som regel en religiøs tekst.
Archimedes´ palimpsest er en kopi fra 900-tallet af forskellige Archimedestekster, hvoraf nogle ellers ikke var bevarede. Det rummede også et par andre tekster. I 1100-tallet forsøgte man så at genbruge pergamentet som ovenfor beskrevet. Heiberg, som fandt det i 1906, lavede sort-hvide fotografier af det, transskriberede det og fik det senere udgivet på græsk.
Siden 1906 har manuskriptet ført en omtumlet tilværelse: Det blev et kostbart samlerobjekt, som gik fra hånd til hånd, indtil
det blev offentlig eje i Walters Art Museum i Baltimore i Maryland, USA. I perioden fra 1998 til 2008 udsatte man palimpsestet for
moderne billedbehandling i form af digital signalbehandling v.hj.a. ultraviolet, infrarødt og synligt lys og røntgenstråler.
Resultatet kan ses nedenfor, eksemplificeret ved en enkelt side:
 |
En typisk side fra Archimedes´ palimpsest |
 |
Palimpestsiden efter moderne billedbehandling |
Om Archimedes´ metode
Archimedes dedicerede sit værk "Om Metoden" til sin ven Eratosthenes, og i forordet står der bl.a.:
"Da jeg (A) anser dig (E) for at være en alvorlig student, en mand af betydelig dygtighed i filosofien og en beundrer af matematiske undersøgelser, anså jeg det for rimeligt i denne bog at beskrive og forklare dig i detaljer de karakteristiske træk ved en vis metode, ved hvis hjælp du vil blive i stand til at undersøge nogle af matematikkens problemer ved mekanikkens hjælp ... Thi visse ting blev først klare for mig ved en mekanisk metode, skønt de senere måtte bevises geometrisk, fordi undersøgelserne af dem ved den nævnte metode ikke udgjorde noget egentligt bevis. Men når vi ved denne metode har erhvervet os noget kundskab til spørgsmålene, er det naturligvis lettere at finde et supplerende bevis, end det er at finde dette uden nogen forudgående viden."
Citatet er gengivet fra Olaf Pedersen og Mogens Pihl: Historisk Indledning til den Klassiske Fysik.
Når Archimedes fik sine ideer, lavede han således tit fysiske ræsonnementer ud fra "forkert, men næsten rigtig" matematik. Bl.a. beskrev han en plan eller rumlig figur, f.eks. en cirkel, ved hjælp af parallelle, tynde stænger, der "næsten" udfyldte figuren. Så anvendte han sine resultater om vægtstænger og tyngdepunkter. Derefter lod han de tynde stænger blive mindre og mindre, - man kalder sådanne "uendelig tynde eller små" tingester for "infinitesimaler". Så "gik han til grænsen" og fandt nu løsningen på det givne problem. Men når han så bagefter skulle skrive om resultatet, benyttede han Platons og Euclids strenge, formalistiske og deduktive metode. Se det, vi har skrevet om "exhaustionsmetoden" i afsnittet om matematik ovenfor.
Astronomi
I modsætning til andre græske forskere arbejdede Archimedes imidlertid ikke ret meget med astronomi. Hans væsentligste bedrift her var, at han i værket "Sandregneren" omtalte Aristarchos´ teori om, at det er Jorden, der drejer sig om Solen, og ikke omvendt. Det er første gang dette heliocentriske synspunkt bliver nævnt i de bevarede kilder, og vi ved ikke, om Archimedes selv troede på det eller ej.
Sandregneren er også spændende, for på trods af, at grækerne havde et anstrengt forhold til tal (igen - muligvis, fordi de havde slaver til det praktiske) og specielt til store tal, så er det i Sandregneren, at Archimedes for første gang i historien skriver om meget, meget store tal!
Betydning
Archimedes påvirkede bl.a. hollænderen Simon Stevin og Galilei. Galilei videreudviklede den matematiske fysik ved at inddrage systematiske eksperimenter og observationer, og så bruge matematiske modeller. Archimedes havde mest brugt tankeeksperimenter. Galilei blev derved skaberen af den moderne fysik.
Archimedes´ infinitesimaler og exhaustionsmetode blev forløberen for Newtons og Leibniz' infinitesimalregning, som har fået en enorm betydning for både matematikken og fysikken (og al moderne anvendt matematik). "Infinitesimalregning" betyder differentialregning + integralregning. Se vores forklaringer under 1670. Det var imidlertid først i slutningen af 1800-tallet, at det formelle grundlag for disse discipliner blev bragt i orden af Weierstrass. Archimedes havde kun forløberen for integralregning, ikke nogen ækvivalent til "differentialregning". Da disse to begreber er forbundet som hinandens omvendte, var hans udregninger af arealer og rumfang mere besværlige end i dag.
Archimedes er én af historiens allerstørste fysikere og matematikere. Han var en forløber for den naturvidenskabelige revolution
i 1500-, 1600- og 1700-tallet.
| Hvis du støder på et ord, hvis betydning du ikke kender, så søg på ordet. |