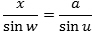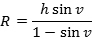Al-Biruni arbejdede inden for mange fagområder. Vi kan ikke komme ind på det hele her, men vi vælger at beskrive nogle udvalgte eksempler:

1. Astronomi Inden for astronomi er han især kendt for to ting: For det første målte han ekliptikakoordinaterne (længde og bredde) for en lang række stjerner. Målingerne blev foretaget med et astrolabium. Og for det andet arbejdede han med Solsystemets struktur. Han hævdede at planeterne bevæger sig i ellipseformede baner, og at der også virker tyngdekraft mellem himmelegemerne. Han indså også, at de astronomiske iagttagelser ligeså godt kunne forklares ved at antage, at Jorden drejer sig om sig selv og går rundt om Solen, som ved det verdensbillede, de fleste troede på dengang. 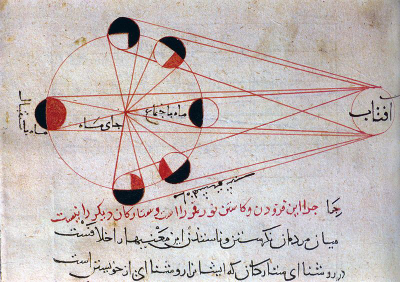Billedet til højre er fra en af al-Birunis bøger, der naturligvis var håndskrevne. Det illustrerer månens faser. Den håndværksmæssige kvalitet er høj.

2. Begrebet vægtfylde er implicit hos Archimedes, men hos al-Biruni møder man for første gang et systematisk studium af begrebet. Vægtfylde kaldes også massefylde og densitet. Et stofs vægtfylde defineres som vægten af en rumfangsenhed, altså f.eks. vægten i gram af en kubikcentimeter af stoffet. I andre kulturer og i gamle dage bruges andre enheder. Da 1 gram er defineret som vægten af 1 cm3 vand har vand vægtfylden 1g/cm3. En portion vand vejer altså lige så meget som dets rumfang. En vægtfylde kan bestemmes ved hjælp af Archimedes lov. Den siger, at når et legeme sænkes ned i vand, mister det lige så meget i vægt, som vægten af den fortrængte væskemængde. Vægttabet er altså lig med legemets rumfang. 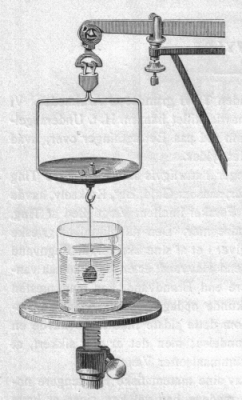På billedet viser vi, hvordan målingen kan foregå. Billedet viser det yderste af den ene arm af en gammel skålvægt. Lad os sige, at vi vil bestemme vægtfylden af kobber. Så tager vi et lille stykke kobber og hænger det op under vægtskålen. -Vandet er der ikke endnu. Vi lægger lodder på den anden vægtskål og finder ud af, at kobberet vejer skal vi sige 135 gram. Så stiller vi skålen med vand som vist på billedet og opdager, at vægtskålen bevæger sig opad. Det hænger sammen med Archimedes lov. Så måler vi vægttabet ved at lægge lodder på den synlige vægtskål indtil der er ligevægt, sådan som det er vist på billedet. Lad os sige, at vægttabet er 15 gram, de to lodder på figuren. Rumfanget af kobberstykket er altså 15 cm3. Heraf følger, at kobbers vægtfylde er 135/15 = 9 g/cm3. Al-Biruni brugte andre enheder, mens ellers var det denne metode, han brugte til vægtfyldebestemmelse. Han bestemte vægtfylden af 18 mineraler, og opdagede også, at saltvand har større vægtfylde end ferskvand.

Her følger en tabel over vægtfylder i g/cm³, sådan som vi kender dem i dag:

ilt	kork	egetræ	olie	vand	magnium	glas	granit	kobber	sølv	guld	platin
0.0014	0,2	0,7	0,8	1	1,7	2,4	2,8	9	10	19	21

Det er mærkeligt, at al-Biruni skrev sine vægtfylder som et helt tal efterfulgt af brøker med tælleren 1 og heltallig nævner ≤ 10. Det var en skrivemåde, der blev anvendt i det gamle Ægypten. Mon der er kontinuitet her??

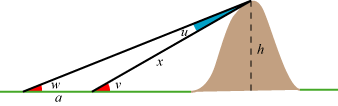
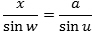
3. Bestemmelse af bjerges højder Al-Biruni opdagede, hvordan man kan bestemme højden af et bjerg uden at gå derop. Han stod nede i det flade land og målte fra to tilfældige punkter retningerne af sigtelinierne til bjergtoppen. Afstanden mellem punkterne kaldes a, og de to røde vinkler kaldes v og w. Så bliver u = v - w og stykket x kan så bestemmes af sinusrelationen, og dernæst er h = x·sinv. Lad os tage et taleksempel: Hvis a = 300 m, v = 10° og w = 8° bliver u = 2°, x = 300·sin8°/sin2° = 1,2 km og h = 1,2·sin10° = 208 meter. En af vores kilder hævder, at det er den første praktiske anvendelse af sinusrelationen.

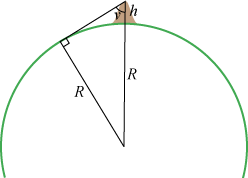
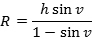
4. Bestemmelse af Jordens størrelse Denne gang er al-Biruni nødt til at gå op på bjerget. Deroppe måler han vinklen v mellem lodlinien og retningen til horisonten. - Det er bedst, hvis bjerget ligger ude ved havet, -eller ved Aralsøen. Af den retvinklede trekant på figuren får vi, at (R + h)sinv = R, hvoraf En af vores kilder nævner, at al-Biruni ved hjælp af denne formel bestemte Jordens rarius til R = 6340 km, hvilket passer fint med det moderne tal 6356 km. Vi tror nu ikke på det. For h = 1 km og v = 88,9° giver formlen R = 5425 km og for v = 89° giver formlen R = 6565 km. Derfor skal vinklen v aflæses med mindst 2 decimalers nøjagtighed, og det ligger langt ud over hvad man kan opnå med et astrolabium. Men selv om al-Biruni skønnede vinklen v til at være 89° ville det jo give et for den tid helt tilfredsstillende resultat. - For øvrigt kan det undre, at man kender den længdeenhed, som al-Biruni anvendte, tilstrækkelig nøjagtigt. Al-Biruni benyttede også triangulering, og i den sammenhæng kan han godt have fundet en bedre værdi af Jordens radius.

Al-Biruni var en af middelalderens mest fremtrædende fysikere!