Forside Søgning Liste

Archimedes vigtigste arbejder var inden for matematik. De er helt vidunderlige, men det skal vi ikke komme ind på her. Men han grundlagde også den matematiske fysik inden for områderne mekanik og hydrostatik.

I sine mekaniske arbejder fremlagde Archimedes resultater om vægtstangen, om tyngdepunkter og om svømmende legemer.

1. Vægtstangen

Archimedes fremstilling af teorien om vægtstangen er formet som en matematisk, deduktiv teori. Det sker sikkert under påvirkning af den succes, som den aksiomatiske metode havde i matematikkens samtidige udvikling. Archimedes bruger 8 aksiomer som grundlag for mekanikken. For at give et indtryk af dem, nævner vi her fire af aksiomerne:

• Lige store vægte ophængt i lige store afstande er i ligevægt.
• Hvis vægte, ophængt i visse afstande, er i ligevægt, og hvis noget tilføjes til én af dem, så vil der ikke længere være ligevægt, men vægtstangen vil gå ned til den side, hvor vægten er forøget.
• Tyngdepunkterne for forskellige, men ligedannede, figurer er placeret i punkter, der svarer til hinanden.
• Tyngdepunktet for en figur, det intet sted er konkav, findes inden i figuren.

Konkav betyder "har en bule indad".

Det høje præcisionsniveau i Euclids elementer havde fra Archimedes tid og helt frem til slutningen af 1600-tallet en meget skadelig indflydelse i fysikken. Man prøvede at anvende en aksiomatisk fremstillingsmåde og baserede fremstillingen på geometri, i stedet for at bruge tallene. Det var ikke godt, for fysik er en erfaringsbaseret videnskab, der bygger på målinger, hvis resultater er tal. Her refererer vi kort nogle af Archimedes´ resultater i vore dages sprog.

En vægtstang er en vandret, vægtløs, stiv stang, der kan dreje sig om en vandret akse C vinkelret på stangen. På stangen kan man forskellige steder hænge vægte, og problemet er følgende: Hvad er betingelsen for, at stangen forbliver i ligevægt, når man hænger vægte på den. Vi starter med at hænge to vægte på stangen:

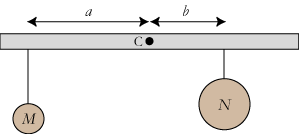
Formodentlig dels ved eksperimenter, dels ved en snedig symmetribetragtning, fandt Archimedes ud af, at hvis man hænger vægten M på stangen i afstanden a fra omdrejningsaksen og på den anden side af aksen hænger vægten N i afstanden b, da er der ligevægt når aM = bN. a og b kaldes vægtenes arme, og produktet vægt gange arm kaldes vægtens moment. Så kan man også sige, at det moment aM, der prøver at dreje stangen den ene vej, skal være lig med det moment bN, der prøver at dreje stangen den anden vej rundt. Det er indeholdt i resultatet, at legemernes form ikke spiller nogen rolle. Det hele afgøres af deres vægte og af ophængningspunkternes placering på stangen. Da ophængningssnorens forlængelse går gennem tyngdepunktet, er det alene tyngdepunktets afstand fra den lodrette linie gennem C, der spiller en rolle for ligevægten. Legemerne kan frit parallelforskydes op og ned, uden at en ligevægt ændres.

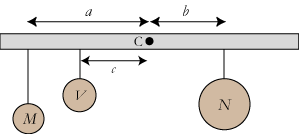
Der er naturligvis også en ligevægtsbetingelse, når der hænger mere end to vægte på stangen. På figuren er der tre vægte, og ligevægtsbetingelsen bliver

aM+cV = bN

Generelt siger vægtstangsreglen følgende:

Ligevægtsbetingelsen for en vægtstang er, at summen af de momenter, der drejer den ene vej, er lig summen af de momenter, der drejer den anden vej.

2. Tyngdepunkt

Archimedes skrift med definition af begrebet tyngdepunkt er gået tabt, men andre bevarede arbejder af ham gør det muligt at rekonstruere i hver fald en del af hans viden om tyngdepunkter. Det handler om faste legemer. De behøver ikke bestå af samme materiale hele vejen igennem, men hvis der f.eks. er en blyklump inde i en træklods, skal den sidde fast derinde, den må ikke kunne rulle rundt i et hulrum. Et legeme, der består af samme materiale hele vejen igennem, kaldes homogent.

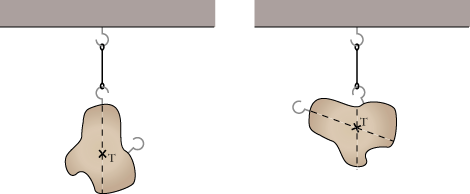
Så opdagede Archimedes, at til et fast legeme hører der et bestemt punkt T, der kaldes legemets tyngdepunkt. Hvis man hænger legemet op i en snor, vil snorens forlængelse altid gå gennem tyngdepunktet. Så tyngdepunktet kan bestemmes ved, at man to gange hænger legemet op i en snor, og begge gange borer et ganske tyndt hul (punkteret på figuren) gennem legemet i forlængelse af snoren. Så vil de to huller møde hinanden i tyngdepunktet. Den ældste bevarede definition af begrebet tyngdepunkt findes i Pappos skrifter. Læs under Pappos. Ved at følge tankegangen ovenfor, kan man finde tyngdepunktet for nogle simple legemer:

Tyngdepunktet for en homogen kugle er i centrum. En homogen ring (en torus) har tyngdepunkt midt i hullet. En tynd homogen stang har tyngdepunkt i sit midtpunkt. En tynd plade, der har form som et rektangel, har tyngdepunkt i diagonalernes skæringspunkt

Hvis man hænger et legeme op i sit tyngdepunkt (- det kan man gøre med en cardansk ophængning, ligesom et skibskompas -), er det i ligevægt i alle stillinger. Og sådan kan man kende tyngdepunktet.

Lad os sætte to ens homogene kugler sammen til ét legeme ved hjælp af en stiv masseløs stang. Det sammensatte legeme får da tyngdepunkt T midt mellem kuglernes centre. Det følger af det tredie aksiom ovenfor.

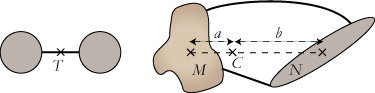
Mere generelt betragter vi to vilkårlige faste legemer med vægtene M og N. Dem sætter vi solidt sammen med et par stive, masseløse stænger. Og så spørger vi: Hvor ligger tyngdepunktet for det nye sammensatte legeme? Ja, det bliver et punkt C på forbindelseslinien mellem de to legemers tyngdepunkter. Og C skal vælges sådan, at

aM = bN

Det nye tyngdepunkt ligger nærmest ved det tungeste legemes tyngdepunkt. Det passer med, at der vil være ligevægt, hvis man bruger linien mellem tyngdepunkterne som vægtstang og en linie gennem C vinkelret på linien mellem tyngdepunkterne som omdrejningsakse.

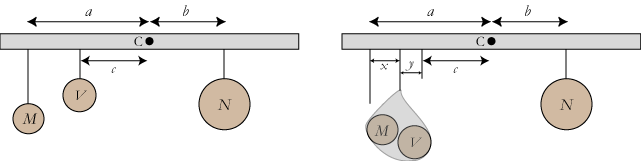
Til venstre på figuren ovenfor viser vi to vægte M og V, der er i ligevægt med en tredie vægt N. Der gælder altså aM+cV = bN. På figuren til højre har vi puttet M og V i en pose og hængt den op i et punkt, der er valgt således, at x/y=V/M. Det er så ikke svært at regne ud, at ligevægtsbetingelsen stadig er opfyldt. Hvis vi tænker os vægtene anbragt på selve vægtstangen, har vi vist, at nogle vægte på en vægtstang kan samles i deres tyngdepunkt uden at ligevægten forstyrres.

3. Tyngdepunkter og infinitesimaler

I dette afsnit vil vi gennemgå Archimedes bestemmelse af tyngdepunktet for en homogen tynd plade af form som en trekant ABC:

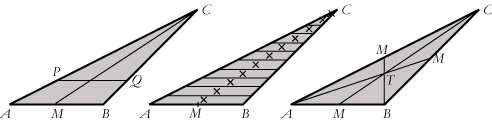
Vi kigger på en trekant ABC og minder om, at en median i trekanten er et liniestykke som CM, der forbinder en vinkelspids C med midtpunktet M af den modstående trekantsside. Hvis PQ er parallel med AB ligger midtpunktet af PQ på CM. For nu at finde trekantens tyngdepunkt deler vi med vandrette linier trekanten i en masse smalle strimler. Så kan vi regne med, at hver strimmels tyngdepunkt ligger i strimlens midtpunkt. Disse tyngdepunkter er markeret med ×-er på den midterste figur. De ligger allesammen på medianen CM. Så begynder vi at lime strimlerne sammen igen: Først limer vi f.eks. de to nederste strimler sammen. Da de to tyngdepunkter ligger på medianen, vil den sammenlimede strimmels tyngdepunkt også ligge på medianen. Og sådan bliver det ved, mens vi limer strimler sammen. Resultatet er, at trekantens tyngdepunkt ligger på medianen CM. Det samme argument viser, at tyngdepunktet ligger på de to andre medianer. De tre medianer fra midtpunkterne M til den modstående vinkelspids har altså et punkt fælles, og dér ligger trekantens tyngdepunkt.

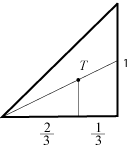Hermed har vi ikke blot fundet trekantens tyngdepunkt, vi har også som et intellektuelt biprodukt bevist, at de tre medianer i en trekant har et fælles punkt, medianernes skæringspunkt. Det er ikke svært at bevise, at stykket fra skæringspunktet og ud til en vinkelspids er 2/3 af hele medianen. Af hensyn til en anvendelse nedenfor nævner vi, at i den retvinklede trekant på figuren ligger tyngdepunktets projektion på den vandrette katete i afstanden 1/3 fra den rette vinkel.

Så kunne man indvende følgende: Når nu de smalle strimler er og forbliver skæve ude i enderne, er det så ikke lidt snyd at regne med, at tyngdepunktet for en stang ligger midt på stangen? Jo, lidt snyd er det vel, men snyderiet bliver jo mindre og mindre, hvis vi laver smallere og smallere stænger. De tynde stænger kaldes infinitesimaler, når de er - øh - uendelig smalle, og det er den uklarhed, som differential- og integralregningen i 1800-tallet fik bragt orden i. Archimedes fik det også bragt i orden ved hjælp af en metode, der kaldes exhaustionsmetoden. Denne metode kræver imidlertid ny hittepåsomhed, hver gang et nyt problem skal løses. I 1600-tallet skabtes differential- og integralregningen, der - når man ellers har lært den - for det meste kan anvendes uden store problemer.

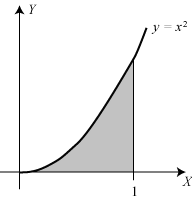Archimedes løste en lang række matematiske problemer ved hjælp af begrebet tyngdepunkt. Vi tager et eksempel, for at illustrere fremgangsmåden: Vi vil finde det grå areal A mellem parablen y=x2 og stykket på X-aksen mellem 0 og 1. For at kunne udnytte begrebet tyngdepunkt tænker vi os, at XY-planen er en tynd plade, hvor en arealenhed vejer en vægtenhed. Vægten af en figur er altså lig med dens areal, og vi skal altså finde vægten af det grå område.

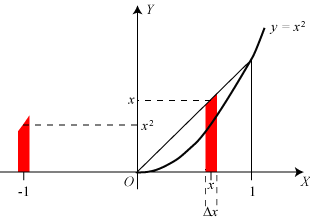Vi vil finde det grå areals vægt ved at sammenligne det med vægten af den viste trekant med vinkelspidser (0,0), (0,1) og (1,1). Vi deler både trekanten og det grå areal op i et stort antal lige brede lodrette strimler. Bredden kaldes Δx, og vi kigger på to af disse strimler, der står på samme stykke af X-aksen. De er røde på figuren. Deres midte ligger i afstanden x fra (0,0). Vi flytter den af de røde strimler, der ligger under parablen, stykket 1+x mod venstre, sådan som det er vist på figuren. Der er altså kun én rød strimmel tilbage til højre, og den har højden x. Så er det så mærkeligt, at hvis vi opfatter X-aksen som en vægtstang med (0,0) som omdrejningspunkt, og tænker os, at stangen er belastet med de to røde strimler, så er der ligevægt: Hvis vi tillader os at se bort fra den lille skævhed for oven har parabelstrimlen til venstre vægten x2Δx og armen er 1, hvis vi ellers har valgt Δx enormt lille. Derfor er momentet x2Δx. Vægten af den røde trekantsstrimmel til højre er xΔx, og armen er x, så momentet bliver x2Δx, altså det samme som før. Der er altså ligevægt.

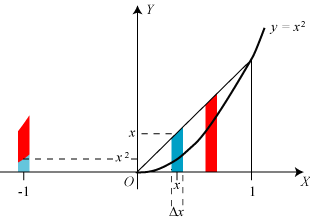Den proces, som vi ovenfor gennemførte for de to røde strimler, gennemfører vi nu igen, denne gang med to blå strimler. Til venstre har vi stillet den blå strimmel foran den røde. De står begge på samme lille stykke af X-aksen. Så er de to blå strimler også i ligevægt, og derfor er der også ligevægt, når vægtstangen belastes med både de røde og de blå stænger. Sådan kan vi blive ved, indtil vi har behandlet alle strimlerne. Resultatet er, hvis vi ellers vælger et enormt lille Δx, at parabelarealet A, skåret i strimler og placeret til venstre, er i ligevægt med trekantsstrimlerne. Som vi så ovenfor, kan vi uden at ødelægge ligevægten samle trekantsstrimlernes vægt i trekantens tyngdepunkt. Trekantvægten er 1/2 og armen bliver 2/3, som vi så ovenfor. Momentet bliver derfor 1/3, og parabelmomentet bliver 1·A. Da de to momenter er lige store er A=1/3.

I argumenterne ovenfor har vi som antydet flere gange lavet fejl, som vi dog kan få så små, som vi vil have dem, ved at vælge Δx tilstrækkelig lille. Derfor har vi fuld tillid til resultatet. Det vil en rigtig matematiker ikke have, han vil have et præcist bevis. Det ville Archimedes også. Så når han ved hjælp af tyngdepunktsmetoden havde fundet et resultat, så publicerede han det ikke. Han lavede et præcist bevis ved hjælp af exhaustionsmetoden (se biografien), og det publicerede han så. Det er en pointe, at exhaustionsmetoden kræver, at man kender resultatet på forhånd, det gør tyngdepunktsmetoden ikke.

4. Svømmende legemers ligevægt.

De snedigste af Archimedes fysiske resultater handler om legemer nedsænket i væske. Vi betragter kun nogle ret overskuelige situationer.

A. Lad os først kigge på et legeme, der er tungere end vand, sådan som det er vist på figuren nedenfor. Det vejer 3 kg, og lad os sige, at det har et rumfang på 1 liter. Det er en velkendt erfaring, at en tung ting bliver lettere at bære, hvis den er under vandet. Spørgsmålet er: Hvor meget har det grå legeme tabt i vægt af at komme ned i vand? Det kan man måle, og i det tilfælde, der er vist på figuren, har legemet tabt sig 1 kg, og vægten under vand er 2 kg. Da rumfanget af legemet er 1 liter, er vægttabet lig vægten af den fortrængte vandmængde U.

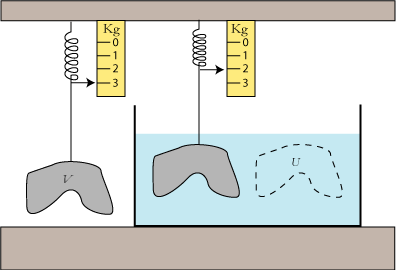
Dette resultat kan mere generelt formuleres sådan:

Hvis et legeme er nedsænket i en væske, er vægttabet lig vægten af den fortrængte væskemængde.

Man kan også tænke sig til resultatet. Det kunne Archimedes i hvert fald: Ved siden af legemet har vi i samme dybde med punktering afgrænset en væskemængde af samme form som legemet. Lad vægten af legemet være V kg, og lad vægten af den punkterede væskemængde være U kg. Nabovanddelene til den punkterede væskemængde trykker på den fra alle sider, og resultatet af dette tryk er, at væskemængden holdes på den plads, den har. Trykket bærer altså præcis vægten U. Men nabovæskedelene til legemet trykker på det på præcis samme måde. De bærer altså U kg af de V kg, som legemet vejer. Så resultatet er, at legemet nede i væsken vejer V-U kg. Vægttabet U kaldes også opdriften. Det er jo det opadrettede resultat af den omgivende væskes tryk på legemet.

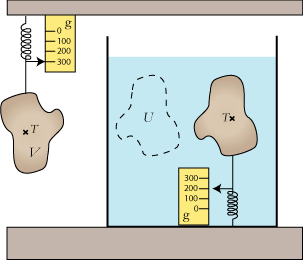
B. Lad os dernæst kigge på et legeme, der er lettere end vand, f.eks. det brune legeme, der er af træ. Vi trykker det ned i vandet og binder det fast til bunden med en fjedervægt. Lad os sige, at legemet vejer 300 g, og at den fortrængte væskemængde vejer 500 g. Ligesom før kan trykket fra nabovanddelene til den punkterede vandmængde bære 500 g. Resultatet af nabovanddelenes tryk på legemet er altså et opadrettet tryk på 500 g. Tyngden hiver nedad i legemet med 300 g, så for at der kan være ligevægt, må fjederen hive nedad med 200 g. Man kan godt sige, at vægttabet er 500 g. Vægten ændres jo fra 300 g i nedadgående retning til 200 g i opadgående retning.

Lad os nu kigge på det generelle tilfælde: Lad os sige, at legemet har vægten V kg, og at den fortrængte væskemængde vejer U kg og at U>V. Der er to spørgsmål:

1. Hvor meget hiver legemet i snoren.
2. I hvilken stilling er der ligevægt?

Svaret på det første spørgsmål er nu let: Vægten i luft er V kg, og vandet trykker opad med U kg, så snoren må hive nedad med U-V kg. Man kan altså sige, at der gælder samme sætning som før.

For at svare på det andet spørgsmål betragter vi tyngdepunkterne for legemet og for den fortrængte vandmængde. Man kan da ved forsøg og også ved udregning vise, at der er ligevægt, når snoren og de to tyngdepunkter ligger på samme lodrette linie. - Det kan godt ske, at dele af legemet befinder sig lavere end ophængningspunktet. Det er en forudsætning, at legemet ikke kommer i vejen for snoren.

C. Vi går nu over til at beskrive, hvad der sker, når vi lader et legeme, f.eks. af træ, flyde på vand. Der er 2 naturlige spørgsmål:

1. Hvor langt synker det ned? 2. I hvilken stilling lægger det sig til hvile?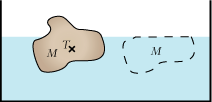

Svaret på det første spørgsmål blev fundet af Archimedes: Legemet synker så langt ned, at det rumfang vand, det fortrænger, vejer lige så meget som legemet. Et stykke træ, der vejer 1 kilo, og som svømmer på vand, har altså 1 liter af sit rumfang under vandoverfladen. Dette resultat kan man tænke sig til næsten ligesom før: Lad os lige under vandoverfladen afgrænse en punkteret vandmængde af samme form og beliggenhed, som den del af legemet, der er under vandoverfladen. Vandet er i ro, så nabovanddelenes tryk på den punkterede vandmængde holder den præcis på plads og i ro. Men nabovanddelene til det svømmende legeme trykker nøjagtigt på samme måde på legemet, og holder det i ligevægt. Derfor må legemet veje lige så meget som den fortrængte vandmængde. Altså:

Hvis et legeme svømmer på en væskeoverflade, og der er ligevægt, da vejer den fortrængte væskemængde det samme som legemet.

Det var svaret på det første spørgsmål. I alle tre tilfælde A, B og C gælder altså Archimedes lov:

Svaret på det andet spørgsmål er mere kompliceret. Det blev først fundet af Stevin i slutningen af 1500-tallet, læs om det under 1586 Stevin.

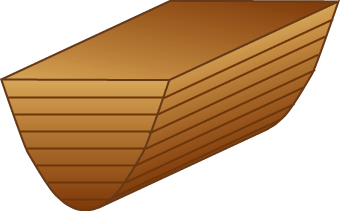Archimedes gennemførte imidlertid én undersøgelse, hvor han besvarede spørgsmålet, og den undersøgelse hører til Archimedes´ allerbedste. Det handler om en lang parabolsk cylinder, sådan som den er vist på figuren. Vi har prøvet at få den til at ligne et skibsskrog, fordi vi gætter på, at det var med henblik på anvendelser inden for skibsbygning, at Archimedes gennemførte sin undersøgelse. Hvis cylinderen er ganske lav og flyder på vand, vil den flyde på med vandret overside, og hvis den er meget høj, vil den tippe over. Det lykkedes Archimedes at finde ud af, hvor grænsen mellem de to situationer går, og han fandt også den vinkel, som oversiden danner med vandret, i de tilfælde hvor cylinderen tipper.

5. Konklusion.

Sammenfattende kan man sige, at det, at Archimedes således beskæftigede sig med fysiske og anvendelige problemstillinger, markerer en afgørende forskel fra de mere filosofisk indstillede græske matematikere.

Hvis du støder på et ord, hvis betydning du ikke kender, så søg på ordet.