Forside Søgning Liste

Definition af en epicykloide.

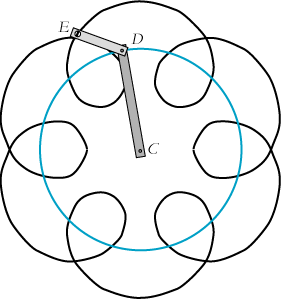
På figuren kan den mørke stang dreje sig om punktet C. Den lyse stang er hængslet til den mørke i punktet D. Vi tænker os, at de to stænger til at begynde med er lodrette opad i forlængelse af hinanden. På et tidspunkt starter vi med at dreje den mørke stang med vinkelhastigheden 50° i sekundet mod uret. (Vinkelhastigheden er det antal grader, som stangen drejer sig på et sekund.) Samtidig starter vi med at dreje den lyse stang omkring punktet D med en vinkelhastighed, der er 7 gange så stor, målt i forhold til en lodret linie. På figuren vises situationen efter 2 sekunders forløb: Den mørke stang har drejet sig 10°, og den lyse har drejet sig 70°. Hvis man under denne bevægelse trykker en blyantsspids ned gennem hullet ved E, vil blyanten tegne den sorte kurve. Den kaldes en epicykel. Du kan få bevægelsen at se herunder.

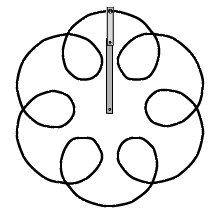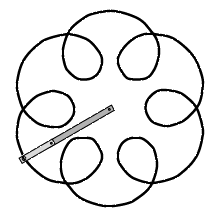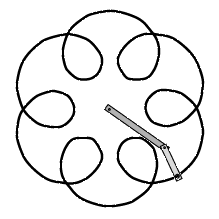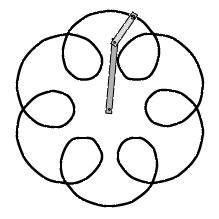
Man kan få andre epicykler frem ved at ændre på stængernes længder og deres rotationshastigheder:

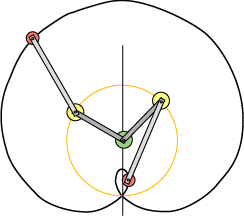
Vi starter igen med to lodrette stænger, men denne gang drejer vi den lyse stang halvt så hurtigt som den mørke. Til venstre har stængerne drejet sig 60° og 30° væk fra startstillingen. Til højre har stængerne drejet sig 316° og 158°. Vi får så tegnet den viste sorte epicykel. En epicykel af denne form blev i oldtiden brugt som en god tilnærmelse til banen for planeten Mars ( - "den røde planet"), - hvis man altså antager, at Jorden står stille. Grunden er, at forholdet mellem stanglængderne er det samme som forholdet mellem radierne for banecirklerne for Mars og Jorden, og at et marsår er ca. to jordår.

Endnu mere komplicerede epicykler får man ved at øge antallet af stænger til 3 eller endnu flere.

Hvis du støder på et ord, hvis betydning du ikke kender, så søg på ordet.