Forside Søgning Liste

1. Indledning

Eratosthenes er den første fysiker, som vi har en omfattende viden om. Vi starter med at beskrive Eratosthenes definition af begreberne bredde og længde. De udgør en slags koordinatsystem på Jordens overflade.

2. Definition af bredde

Vi vil nu definere hvad bredden af et punkt P på Jordens overflade er. Billedet til højre viser den cirkel på Jordens overflade, der går gennem Nordpolen og Sydpolen og P. C er Jordens centrum. Den vinkel b, der er vist på billedet defineres så som bredden af P. Hvis P ligger på den sydlige halvdel af Jorden defineres dets bredde som -b. Hvis man tænker sig, at cirklen på billedet drejer sig en omgang omkring NS-linjen beskriver P en vandret cirkel, der indeholder alle de punkter, der har bredden b. Alle punkter på Jordens overflade ligger altså på en bestemt breddecirkel; Nordpolen og Sydpolen har bredde 90° og -90° så de ligger ikke på nogen breddecirkel. På det øverste billede nede i afsnit 5 er cirklerne med følgende bredder vist: 0°, ±13°, ±26°, ±39°, ±52°, ±65° ±,78°; 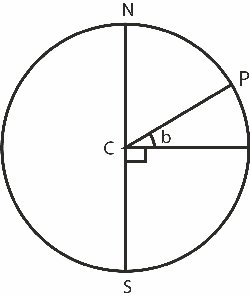de er vist som rette linjestykker.

3. Definition af længde

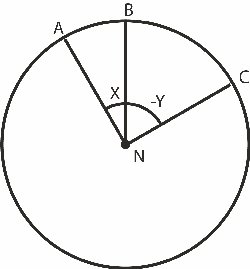Billedet til venstre forestiller Jorden set ovenfra, N er altså Jordens Nordpol og sydpolen S kan ikke ses på billedet. På Jorden ligger så en halvcirkel NBS. Vi vil måle længderne ud fra denne halvcirkel. Punkterne på den siges at have længde 0. I dag går denne halvcirkel gennem London, men det valg ville Eratosthenes selvfølgelig ikke træffe. I stedet træffer jeg her det valg, at jeg lader den øverste kvartcirkel gå gennem Rom, som Eratosthnes utvivlsomt kendte. Alle punkterne på halvcirklen NAS siges så at have længden X, hvor X er den vinkel, der er vist på figuren. (Når to kurver skærer hinanden, defineres vinklen mellem dem i deres skæringspunkt som vinklen mellm deres tangenter i skæringspunktet.) Længere til højre på billedet findes der på Jorden en halvcirkel NCS, hvis plan danner vinklen Y med planen NBS. Punkterne på halvcirklen NCS siges så at have længden -Y. Billedet øverst i afsnit 5 forestillet Jorden med nordpolen for oven og sydpolen for neden. På det billede er der tegnet 11 længdekurver. Den midterste er længdekurven gennem Rom.

4. Bestemmelsen af Jordens størrelse

På billedet til højre illustrerer vi den metode Eratosthenes brugte. Eratosthenes vidste, at der i Syene ( - det nuværende Aswan - ) var en brønd, på hvis bund Solen skinnede om middagen ved sommersolhverv. Det betyder, at man i Syene på denne tid har Solen lige over hovedet. Han målte så i Alexandria, der ligger stik nord for Syene, på samme tid den øverste af de to afmærkede ligestore vinkler, og fandt at Solen var ca. 1/50 af 360° syd for Alexandrias lodlinie. Derfor må Jordens omkreds være 50 gange afstanden mellem Alexandria og Syene. Nøjagtigheden er høj, det korrekte tal er 45 gange. Hvis vi tænker os at Erathostenes benyttede en 1 meter lang lodret stang, så vil skyggen være ca 12 cm lang, og den skulle Eratosthenes nok kunne måle med en nøjagtighed på 1-2 cm.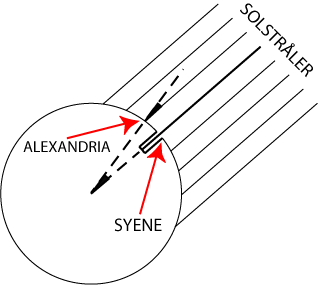

Oven for står der "på samme tid". De to byer Syene og Alexandria ligger ca 70 km fra hinanden. Da man ikke havde ure på Eratofthenes tid, er det nærliggende at spørge om, hvordan Eratosthenes kunne vide, at de to observationer blev foretaget samtidig. Jeg gætter på, at Eratosthenes godt vidste, at Solen på en bestemt længdegrad står højest på himlen samtidig på alle breddegrader. Da Syene og Alexandria ligger på samme længdegrad, var det derfor nok for Eratosthenes at måle Solens maksimale højde i Alexandria på den dag, hvor det var sommersolhverv, typisk den 21. juni. Det spiller ingen rolle, om Eratosthenes tog fejl med nogle få dage.

Eratosthenes resultat, at Jorden er kugleformetblev ikke kendt eller accepteret i Middelalderen. Billedet ovenfor viser den middelalderlige verden, sådan som man opfattede den i 1280, da kortet ovenfor blev tegnet af en engelsk præst. Han delte tidens almindelige opfattelse, at Jorden er flad som en pandekage. Jerusalem blev placeret i verdens centrum, ved et 1-tal. Øverst oppe mod øst ved et 2-tal er Edens Have (Paradiset) placeret. Nederst nede ved 6-tallet findes London; skråt oppe for Londan er Paris angivet ved tallet 5.

5. Længde og bredde på Jorden

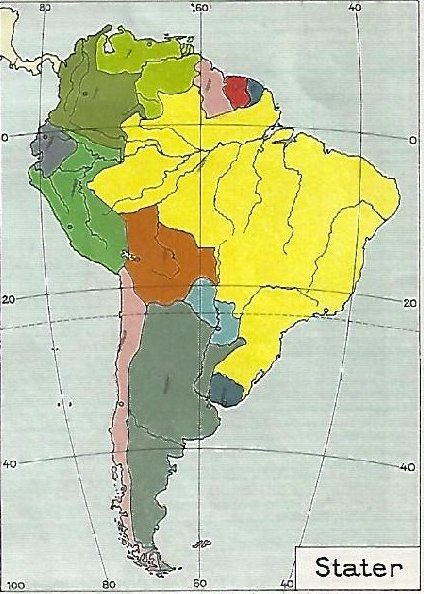
Billedet til højre forstiller Jorden. Det punkt, der ligger højest oppe er Jordens Nordpol, og det, der ligger længst nede er Sydpolen. Når man ser på en breddekurve fra et punkt, der ligger langt væk i kurvens plan, ser man breddekurven som et vandret linjestykke, men hver breddekurve er altså en cirkel. På billedet er der tegnet 13 breddekurver. På billedet er der også tegnet 11 længdekurver. Den midterste går gennem Rom. Det kan man se på det lille farvede kort. Det kort er tegnet ind i korrekt størrelse og placering. Det blå er middelhavet. Det lille farvede billede giver et godt indtryk af, at Eratothenes kun havde kendskab til en meget lille brøkdel af Jordens overflade.

Når man i vore dage i bøger bringer kort, er det almindeligt, at man også tegner et udvalg af de relevante længde- og breddekurver. Billedet til venstre har vi hentet fra en lærebog i geografi fra 50-erne; i den kan man tydeligt se kurverne og de tal, der viser koordinaterne. I moderne atlasser er kurverne og tallene så små, at de bliver ulæselige når jeg scanner et kort ind. Formen på kurverne afhænger af den måde man har valgt at kortlægge det krumme land på et plant kort. Det er en meget kompliceret proces, som vi ikke kan komme nærmere ind på her. På billedet kan man se udløbet af Amazon, Jordens største flod. Hvert sekund løber der 180 tusinde kubikmeter vand ud i Atlanerhavet, det er 4 gange så meget, som der løber ud af den næststørste flod. På kortet kan man se, at Amazons udløb befinder sig nøjagtigt på Jordens Ækvator; et sjovt tilfælde. Eller hvad? Dengang man troede, at Verden var skabt af Gud, var det helt naturligt, at Gud havde anbragt mundingen af Verdens største flod på Verdens største breddecirkel!

6. Døgn, år og skudår

På billedet til højre viser vi Jorden i dens bane om Solen. På 1 døgn drejer Jorden sig 360° omkring den skrå akse, der peger op mod polarstjernen; det er definitionen af et døgn. På sådan et døgn bevæger Jorden sig et ganske lille stykke i dens bane omkring Solen. På et år bevæger den sig én gang rundt i banen. Det er definitionen af et år. De to tidsperioder har intet at gøre med hinanden, så et år er ikke et helt antal døgn.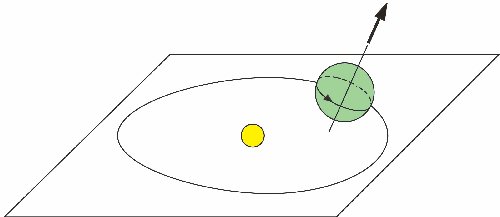

På Eratosthenes tid fandt der olympiske lege sted. Han vidste at det var afgørende for arrangørerne at der var præcis et år mellem to starttidspunkter. Det gav Eratosthenes to værdifulde oplysninger. For det første fik han at vide at arrangørene antog at et år indeholdt 365 dage. Og for det andet kunne han regne ud, at dette år indeholdte for få døgn. Men hvis han tilføjede et døgn, fik man et år, der var for langt. Eratosthenes løste dette problem ved at tilføje et ekstra døgn hvert fjerde år. Det kaldes et skudår. At det netop skulle være hvert fjerde år må Eratosthenes have fundet ud af ved en række forsøg på at finde en god løsning.

Løsningen var holdbar. Den blev officielt indført af den romerske kejser Julius Cæsar i år 45 før Kr., og den gælder her i Danmark stadigvæk; den 29. februar findes kun hvert fjerde år.

7. Konstruktion af en armillarsphære

På billedet til venstre viser vi en armillarsphere. I vores omtale af Tycho Brahe fortæller vi, hvordan Tycho Brahe benyttede armillarspheren, men vores kilder fortæller at Eratosthenes også konstruerede en armillarsphere. Billedet til venstre viser hvordan den armillarsphere, som Erastosthenes konstruerede, kunne have set ud. Armillarspheren skal stilles og instilles sådan, at pilen peger i retning af Himlens Nordpol. Det handler om at kortlægge stjernehimlen, og det er jo helt naturligt at Eratosthenes også gik i gang med denne opgave. Den cirkelring, hvis plan står vinkelret på aksen svarer til Himlens ækvator. Når man sigter på en stjerne på den rigtige måde, kan man aflæse stjernenes koordinater. Man ved vist ikke, hvordan Erastosthenes definerede koordinaterne.

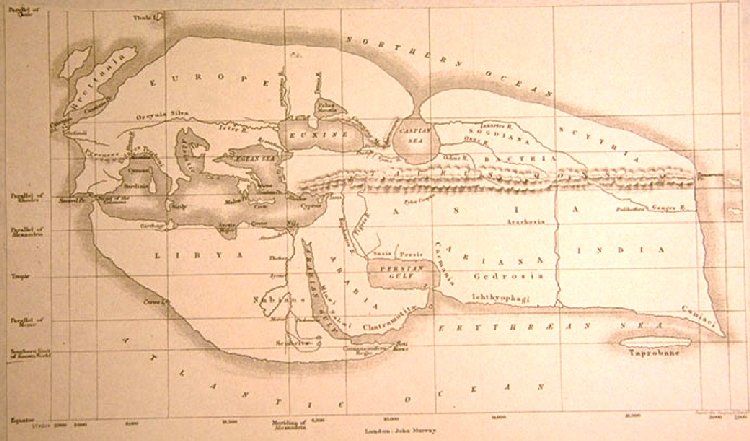
På billedet oven for viser vi et senere kort over den del af Jorden, som Eratosthenes kendte. Jeg ved ikke hvornår kortet er lavet, men det er på mange måder morsomt: For oven til venstre er der en lillebitte ø, der hedder Thule, en gammel betegnelse for en lykkelig ø ved Verdens nordligste grænse; det kunne være Island! Europe, altså Europa, er tegnet som en stor sammenhængende verdensdel nord for middelhavslandene, men Brittanien er ikke tegnet som en del af Europa! Afrika hedder Libya, en verdensdel hvis indre er ukendt undtagen der, hvor Nilen løber. Indien er tegnet som en del af Asien, og sydpå har vi Atlantic Ocean.

Hvis du støder på et ord, hvis betydning du ikke kender, så søg på ordet.