Forside Søgning Liste

Grækerne opdagede tidligt tilbagekastningsloven, allerede Aristoteles kendte den. Heron var vist den første, der formulerede den præcist.

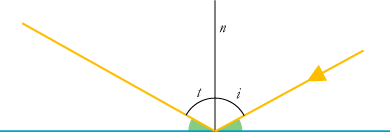
Figuren viser en lysstråle, der rammer et spejl. Indfaldsloddet n er linien vinkelret på spejlet i det punkt, hvor lysstrålen rammer spejlet. Tilbagekastningsloven siger da, at indfaldsvinklen i er er lig med tilbagekastningsvinklen t. De to grønne vinkler er derfor også lige store. De to lysstråler og n ligger i samme plan. Ptolemæus var den første, der efterviste tilbagekastningsloven ved systematiske eksperimenter.

Heron opdagede en anden smuk egenskab ved lysets tilbagekastning:

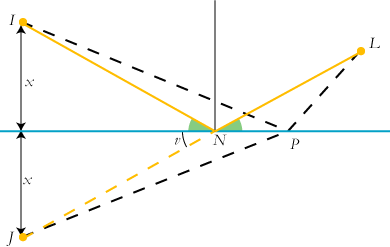
En lysstråle fra lysgiveren L rammer et spejl i punktet N. Strålen tilbagekastes til iagttageren I således at de to grønne vinkler er lige store. Der gælder da følgende:

Den vej lyset følger fra L til I er kortere end enhver anden vej fra L til I via spejlet.

Dette kan man indse på følgende måde: Lad P være et punkt af spejlet, som ikke falder sammen med N. Vi skal da vise, at vejen LPI er længere end LNI. Lad J være det matematiske spejlbillede af I. Det betyder, at de to afstande x er lige store, og at linien IJ er vinkelret på spejlet. Så er vinklen v lig med de to grønne vinkler, og derfor er vejen LNJ en ret linie og den har samme længde som lysets vej fra L til I. På samme måde er den punkterede vej LPI lige så lang som vejen LPJ, og den er jo længere end den retlinede vej LNJ. Lyset vælger altså den korteste vej!

Hvis du støder på et ord, hvis betydning du ikke kender, så søg på ordet.