Forside Søgning Liste

Hvis man på en globus afbilder stjernerne i stedet for landene, får man himmelkuglen. Lidt mere præcist kan man sige sådan: Tegn en streg fra kuglens centrum til en stjerne. Der hvor stregen skærer kuglen, skal stjernen indtegnes. Det gør man til samme tidspunkt med alle stjerner, og derved får man de velkendte stjernebilleder afbildet på himmelkuglen. Himmelkuglen kan tegnes således:

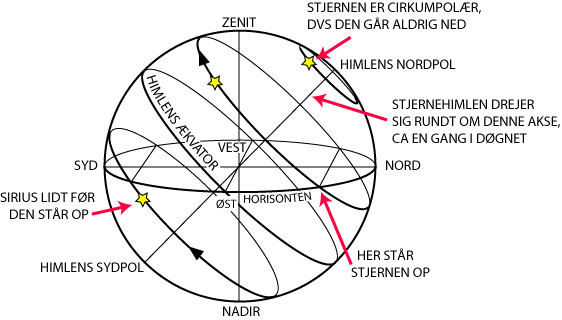
Den vandrette storcirkel kaldes horisonten. Den indeholder de stjerner, der til det betragtede tidspunkt står i horisonten. Det øverste punkt af himmelkuglen kaldes zenit. Det er det punkt, som iagttageren har lige over hovedet. Det nederste punkt kaldes nadir. Den plan, der indeholder nord-syd linien og zenit og nadir, kaldes meridianens plan.

Stjernerne står som bekendt ikke stille på himlen. Hele stjernehimlen drejer sig ca en gang i døgnet om himlens nordpol, lige i nærheden af hvor Polarstjernen står. Det diametralt modsatte punkt kaldes himlens sydpol, og linien, der forbinder polerne, kaldes verdensaksen. Den ligger i meridianens plan. Vinklen mellem horisontens nordpunkt og himlens nordpol er lig iagttagerens breddegrad. Den storcirkel, der ligger i en plan vinkelret på verdensaksen, kaldes himlens ækvator. Himlens ækvator er også tegnet ind på figuren. Himlens ækvator indeholder de stjerner, der står op i stik øst. Det er de samme stjerner, der står lodret over Jordens ækvator. Hvis man nemlig tænker sig, at en lille kopi af Jorden er anbragt midt inde i himmelkuglen med omdrejningsakse på verdensaksen, så ligger Jordens ækvator i samme plan som himlens ækvator. Den tilsyneladende omdrejning skyldes, som vi nu ved, at Jorden drejer sig om sin akse. Himmelkuglen med alle stjernerne på drejer sig altså om verdensaksen en gang rundt på ca et døgn, i pilenes retning. Den tid, som stjernerne bruger til at dreje en gang rundt, kaldes et stjernedøgn. Det er ca 4 minutter kortere end et almindeligt soldøgn. Lad os give en forklaring på, hvordan det hænger sammen.

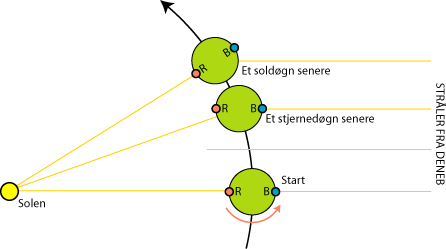
Vi vælger en bestemt stjerne, f.eks. Deneb i Svanen. Så stiller vi to iagttagere, R og B, f.eks. på diametralt modsatte punkter af Jorden. Vi vælger et starttidspunkt, så både Deneb og Solen står i meridianen og har kulmination, dvs maksimal højde over horisonten samtidig. R skal råbe: "Nu" hver gang Solen kulminerer, og B skal råbe: "Nu" når Deneb kulminerer. Så i startøjeblikket råber R og B "Nu" samtidig. Så går tiden i tavshed, men efter et stjernedøgns forløb råber B sit "Nu" fordi Deneb igen er i meridianen. Men R må vente lidt før Solen kulminerer i Meridianen. Et stjernedøgn er altså lidt kortere end et soldøgn. Så efterhånden som tiden går, vil der gå længere og længere tid fra B råber nu til R råber nu. Men når der er gået et år, står Jorden igen i startpositionen, så nu råber de igen Nu! samtidig, så nu har B råbt nu én gang mere end R. Et år indeholder altså et stjernedøgn mere end soldøgn. Lad x være det antal minutter, som et stjernedøgn er kortere end et soldøgn. Så er

Heraf fås, at

Den bue, en stjerne gennemløber fra opgang til nedgang, kaldes dagbuen, resten af dens bane kaldes natbuen. Hvis en stjerne er nord for ækvator, er dens dagbue længere end natbuen. Syd for ækvator er det omvendt.

Hvis man laver en himmelglobus med alle stjernerne på, kan den bruges over hele Jorden. Hvis man ellers kan se dem over horisonten, er stjernebillederne de samme over hele Jorden. Men den hældning, som verdensaksen har, varierer fra sted til sted på Jorden. Hos os i Danmark på 56° nordlig bredde er der 56° fra den nordlige horisont til himlens nordpol. Så hvis man indtegner ækvator på en himmelkugle, duer den kun på en bestemt breddegrad.

Hvis man ikke er interesseret i stjernernes daglige bevægelse, men i stedet vil beskrive Solens årlige bevægelse mellem stjernerne og planeternes mere komplicerede bevægelser, så plejer man at tegne himmelkuglen med vandret ækvator og stillestående stjerner:

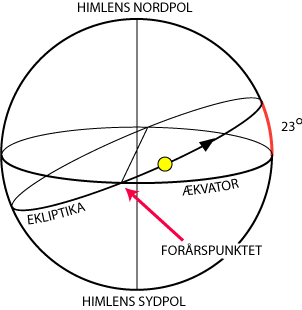
Solens årlige bevægelse mellem stjernerne er ikke helt simpel at iagttage. Man kan jo normalt ikke se stjernerne, når Solen er på himlen. I oldtiden brugte man undertiden Månen som mellemled. En morgen, inden solopgang, målte man Månens placering mellem stjernerne. Og efter solopgang, mens månen endnu var på himlen, målte man Solens placering i forhold til Månen. Derefter kunne man beregne, hvilke stjerner Solen stod iblandt. Mange gentagne målinger af denne art afslørede så, at Solen på et år bevæger sig nogenlunde jævnt på en storcirkel én gang rundt mellem stjernerne. Denne storcirkel kaldes ekliptika. Den danner en vinkel på 23° med ækvator. På figuren kan man se ekliptika, og pilen viser, hvilken vej Solen går rundt. Normalen til ekliptikas plan i himmelkuglens centrum skærer himmelkuglen i to punkter, der kaldes ekliptikas poler.

Før Hipparch regnede man ekliptika som en helt fast storcirkel mellem stjernene. Ekliptika går gennem dyrekredsens stjernebilleder: Vædderen, Tyren, Tvillingerne, Krebsen, Løven, Jomfruen, Vægten, Skorpionen, Skytten, Stenbukken, Vandmanden og Fiskene. Det halvår, hvor Solen er nord for ækvator, er sommerhalvåret hos os, for når Solen er nord for ækvator er dagen længere end natten. Det punkt på ekliptika, hvor Solen krydser ækvator fra syd til nord, kaldes forårspunktet; Solen står i det punkt ved forårsjævndøgn. Det var Hipparchs store opdagelse, at forårspunktet ikke ligger helt fast på ekliptika, men bevæger sig en gang rundt på ekliptika i løbet af 26000 år. Egentlig foregår der det, at Jordens omdrejningsakse i løbet af 26000 år beskriver en omdrejningskegle, hvor omdrejningsaksen er normal til ekliptikas plan. Denne bevægelse kaldes præcessionen.

Ligesom man bruger længde og bredde på Jorden, når man skal fastlægge et steds beliggenhed, har man også koordinatsystemer på himmelkuglen. Faktisk bruger man to forskellige koordinatsystemer:

Ekliptikakoordinater	Ækvatorkoordinater
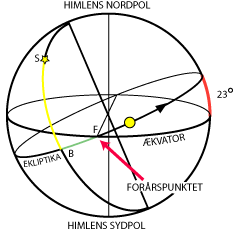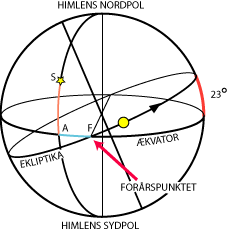Ekliptikakoordinaterne for en stjerne kaldes længden λ og bredden β. For at definere dem forbindes ekliptikas poler med en halv storcirkel, der går gennem stjernen. Den skærer ekliptika i et punkt B. Længden λ for stjernen S er da den grønne bue FB, målt i grader. Den ligger mellem 0° og 360°. Stjernens bredde β er den gule bue BS, målt i grader. Den regnes negativ nedad, så den ligger mellem -90° og +90°.	Ækvatorkoordinaterne for en stjerne kaldes rektascensionen α og deklinationen δ. For at definere dem forbindes ækvators poler med en halv storcirkel, der går gennem stjernen. Den skærer ækvator i et punkt A. Rektascensionen α for stjernen S er da den blå bue FA, målt i grader. Den ligger mellem 0° og 360°. Stjernens deklination δ er den røde bue AS, målt i grader. Den regnes negativ nedad, så den ligger mellem -90° og +90°.

Da man kender de to koordinatsystemers beliggenhed i forhold til hianden, kan man regne det ene sæt koordinater ud, når men kendet det andet.

Præcessionen betyder, at forårspunktet flytter sig en gang rundt på Ekliptika i 26000 år, dvs 50 bueskunder om året. En stjerne med ekliptikakoordinaterne (λ,δ) har derfor et år efter koordinaterne (λ + 50",δ). Ethvert stjernekatalog, der benytter ekliptikakoordinater, skal derfor være forsynet med et årstal, men så er det til gengæld let for brugeren at regne den aktuelle værdi af λ ud. I modsætning hertil er den ændring i en stjernes rektascension og deklination, som præcessionen giver anledning til, kompliceret at beregne. Derfor indså allerede Hipparchos, at man i stjernekataloger bør benytte ekliptikakoordinater.

Såvidt man ved, var det Tycho Brahe, der lavede den første himmelglobus:

Tycho Brahes himmelglobus

Ækvator og ekliptika er tegnet ind på globen. Man kan også se et par af dyrekredsens stjernebilleder: Tvillingerne, Krebsen og Løven.

Hvis du støder på et ord, hvis betydning du ikke kender, så søg på ordet.