Forside Søgning Liste

INDHOLD:
1. Hulspejlet
2. Camera obscura
3. Sfærisk aberration
4. Øjet

1. Hulspejlet

Det har været svært for os at finde ud af, hvem der først fandt de grundlæggende egenskaber ved hulspejle. Den arabiske fysiker Ibn al-Haitham (Alhazen) arbejdede med hulspejlet, men vi ved ikke, præcis hvor langt han kom. Han angav en geometrisk konstruktion af spejlbilledet af et objekt. Her gengiver vi hans resultater i moderniseret form.

Vi tager en kugleskal, der er spejlende på indersiden. Den skærer vi et lille stykke ud af, og smider resten væk. Så står vi med et hulspejl. Vi vælger en akse a, det er en linie, der starter i et punkt A af spejlet og går gennem kuglefladens centrum C. På figuren nedenfor viser vi et snit i hulspejlet, der indeholder den valgte akse a.

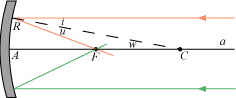
Lad os kigge på en rød lysstråle, der er parallel med aksen; den rammer spejlet i punktet R. Når man skal finde ud af, hvordan denne stråle tilbagekastes fra spejlet, skal man tegne spejlets normal i punktet R. Det er den punkterede linie gennem den oprindelige kugles centrum C. Så bruger vi tilbagekastningsloven om at indfaldsvinklen i er lig udfaldsvinklen u, og tegner den tilbagekastede røde stråle så de to vinkler i og u er lige store. Den tilbagekastede stråle skærer aksen i et punkt F. Da aksen og den røde stråle er parallelle, er vinklerne u og w lige store, så trekant RCF er ligebenet, RF=FC. Og nu kommer der så en tilnærmelsesbetragtning, som man bruger igen og igen i optikken: Når den indfaldende røde stråle er tæt på aksen, kan vi regne de to afstande FR og FA for lige store. F er derfor midtpunktet af liniestykket AC. F kaldes brændpunktet svarende til den valgte akse a, og afstanden f=AF kaldes spejlets brændvidde. Det er halvdelen af den oprindelige kugles radius. Det vi har vist er at

Hvis man retter en akse i et ikke helt lille hulspejl mod Solen, og holder et lille stykke papir i F, så går der ild i papiret. Derfor hedder F et brændpunkt.

Ifølge tilbagekastningsloven kan strålegangen vendes. Så hvis man anbringer en punktformet lysgiver i brændpunktet F, så vil alle de tilbagekastede lysstråler være parallelle med aksen gennem F.

Figuren nedenfor viser, hvad der sker med et andet parallelbundt af blå stråler. De kastes tilbage gennem det brændpunkt F₁, der hører til strålernes retning.

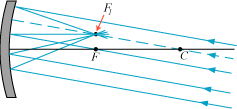
På figuren ligger F₁ med god tilnærmelse lodret over F.

Ovenfor betragtede vi et bundt af parallelle lysstråler og fandt, hvordan de blev tilbagekastet. Nu går vi over til at betragte en punktformet lysgiver, der er placeret i et tilfældigt punkt P. Vi vil finde ud af, hvordan strålerne fra P bliver kastet tilbage fra hulspejlet. Det specielle tilfælde, hvor lysgiveren er anbragt i C, er simpelt. For så er hver af lysstrålerne vinkelret på spejlet, og alle strålerne kastes derfor tilbage i sig selv. På figuren nedenfor viser vi det mere interessante tilfælde, hvor P ligger længere væk fra spejlet end C.

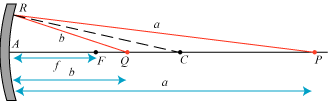
Vi vælger en tilfældig stråle fra lysgiveren i P til spejlet i R, og konstruerer den tilbagekastede lysstråle, så indfaldsvinkel bliver lig udfaldsvinkel. Den tilbagekastede lysstråle skærer aksen i Q, og vi vil nu prøve at finde afstanden b fra spejlet til Q udtrykt ved afstanden a fra spejlet til P. Spejlets brændvidde f skal naturligvis også være kendt. Som ovenfor forudsætter vi, at R ligger så tæt ved A at man kan regne med, at PR=PA=a og at QR=QA=b, sådan som det også er vist på figuren. Det afgørende hjælpemiddel er nu en sætning fra matematikken, der i vores tilfælde siger, at da den punkterede linie er vinkelhalveringslinie i trekant PRQ, da vil

Men da PC=a-2f og QC=2f-b får vi følgende formel:

Den kan nu blive pænere. Vi multiplicerer på begge sider af lighedstegnet med (2f-b)/a og får, at

Slutresultatet fås nu ved at dividere med 2f og omordne leddene:

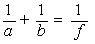Denne spejlformel styrer billeddannelsen i et hulspejl. Først og fremmest kan man se, at b, og dermed beliggenheden af Q kan beregnes, når a og f er kendte. Alle stråler fra P vil derfor efter tilbagekastningen gå gennem samme Q. Hvis man holder et lille stykke papir i Q ser man et billede af P på den side af papiret, der vender mod spejlet. Q kaldes billedet af P.

Hvis P flyttes længere og længere mod højre, og a nærmer sig uendelig, bliver 1/a næsten lig 0, og af spejlformlen ses da, at b nærmer sig f. Hvis P omvendt rykkes ind mod C nærmer Q sig C fra den anden side. Og så kan strålegangen vendes, så når lysgiveren P rykker fra C mod F, så rykker billedet Q fra C og ud i det uendelig fjerne.

Billedet af P kan også findes geometrisk, med en nydelig konstruktion, der skyldes Alhazen:

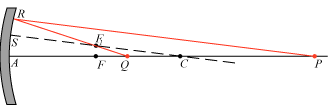
Vi vælger en tilfældig rød stråle PR ud fra P og tegner punkteret aksen SC svarende til strålens retning. Brændpunktet F₁ svarende til den retning er midtpunktet af CS. Og så kastes den røde stråle som vist tilbage gennem F₁, og billedpunktet Q findes ved skæring af PA med RF₁.

Nedenfor viser vi hvordan et billede af en udstrakt genstand kan konstrueres. Læg mærke til, at hvis genstanden er længere væk end centrum, da er billedet formindsket. Hvis genstanden er nærmere spejlet end C, da er billedet forstørret. I begge tilfælde er billedet vendt på hovedet.

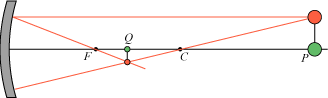
Endelig kigger vi på en genstand, der er nærmere spejlet end brændpunktet. Her er billeddannelsen helt anderledes. Man kan nemlig vise, at strålerne fra et bestemt punkt P af genstanden tilbagekastes i sådanne retninger, at deres forlængelser bag spejlet har et fælles punkt Q. Q kaldes et indbildt billede af P. Øjet ser faktisk Q som et billede af P, idet strålerne fra P efter tilbagekastningen ser ud som om de kommer fra Q. Figuren nedenfor viser konstruktionen af billedet under anvendelse af de sædvanlige stråler. Billedet er retvendt, forstørret og indbildt; det kan ikke opfanges på en skærm.

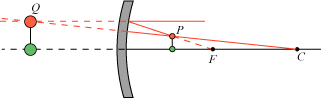
Hulspejle bruges i dag i billygter, i visse typer af badeværelsesspejle, i lyskastere og i spejlteleskoper. Men tit er de cirkelformede spejle erstattet med spejle formet efter en parabel. Billederne nedenfor viser billeddannelsen i praksis.

Flaget er anbragt inden for brændpunktet	Flaget er anbragt uden for brændpunktet

2. Camera obscura

Det fortælles (- men det er nok en røverhistorie), at en dag al-Haitham sad inde i sit telt, opdagede han, at der var et lille hul i teltdugen. Og så så han til sin overraskelse, at på den modsatte teltvæg var der et billede af det, der var uden for teltet. Billedet var omvendt og formindsket, sådan som det er vist på billedet nedenfor.

Al-Haitham studerede fænomenet og gav en beskrivelse af det, som senere blev oversat til latin og kendt i Middelalderens Europa under navnet camera obscura, "det mørke rum". Det er derfor det i dag hedder et digitalt kamera, selv om der ikke er meget mørkt rum i det mere.

3. Den sfæriske aberration

Hvis man tager et hulspejl, der har form som et ganske lille stykke af en kugleflade, vil et parallelbundt af lys med meget god tilnærmelse tilbagekastes gennem brændpunktet, der ligger halvvejs ude mod centret. Men kun med tilnærmelse. Jo større del af kuglen man tager, des større bliver fejlen. Dette fænomen kaldes den sfæriske aberration. Vi ved ikke, hvor meget al-Haitham fandt ud af om den sfæriske aberration, men vi gennemgår her hovedresultatet, fordi argumentet er så elegant. I det følgende betragter vi en spejlende halvcirkel i stedet for en halvkugle.

Praksis: Her skinner sollyset ned i en kagedåse med spejlende inderside. Vi har lagt et stykke hvidt papir ned i bunden af dåsen, så er det lettere at se lyset.

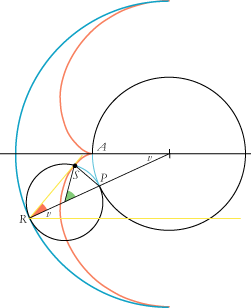På figuren til venstre kigger vi på den blå halvcirkel, der er spejlende på indersiden. Den har radius r. Vi tænker os, at den rammes af et parallelbundt af lys fra højre. Vi kigger på en tilfældig af lysstrålerne. Den rammer spejlet i punktet R. Vi tegner linien fra R til centret. Den vinkel, den danner med de vandrette linier, kaldes v. På figuren er der tegnet yderligere to cirkler C og D. C har radius ½ r og den har samme centrum som spejlet. D har radius ¼ r. Den rører indersiden af spejlet i punktet R, og punktet S sidder fast på D. Vi tænker os, at D ruller på ydersiden af C på den måde, at ved rulningens start falder S sammen med A. Den nederste del af den røde kurve er den banekurve, som punktet S beskriver ved rulningen. Under rulningen er de to blå cirkelbuer hele tiden lige lange. Nu tegner vi linien RS. Den har to vigtige egenskaber: 1. RS er tangent til den røde kurve i punktet S. Et præcist bevis for dette kræver lidt avanceret matematik, men anskueligt er det ret klart: RS er vinkelret på SP, og lige omkring det betragtede øjeblik er rulningen en drejning om P. Derfor må RS være tangent til den røde kurve i punktet S. 2. Da de to blå buer er lige lange, må den grønne vinkel være 2v. Men så må den røde vinkel være v. RS er altså ifølge tilbagekastningsloven den tilbagekastede lysstråle.

Teori: Og ved hjælp af denne figur kan man finde ud af, hvad det er for en lysende kurve man kan se på bunden af kagedåsen

Nu har vi altså indset, at alle de tilbagekastede lysstråler er tangenter til den røde kurve. Derfor er den røde kurve ekstra kraftigt belyst. Yderligere ligger det meste af tangenterne til den røde kurve i området til venstre for kurven. Dette område vil derfor være kraftigere belyst, end området til højre for kurven. Begge dele er i fin overensstemmelse med udseendet af det øverste billede. Kurven kaldes en "kaustisk kurve". Den er en epicykel* frembragt af de to stænger, der begrænser den grønne vinkel.

4. Øjet

Før Alhazen havde man kun meget diffuse forestillinger om øjets funktion, og de ideer man havde, var baseret på spekulationer. Alhazen derimod snitter i et øje, og beskriver de enkelte dele fornuftigt. Han indser, at fra et punkt af den iagttagne genstand må et strålebundt, der udfylder pupillen, nå ind i øjet. Han beskriver også linsen indenfor pupillen, men tror fejlagtigt, at den er selve synsorganet. Først Leonardo da Vinci beskriver øjet som en slags mørkekammer.

Hvis du støder på et ord, hvis betydning du ikke kender, så søg på ordet.