Forside Søgning Liste

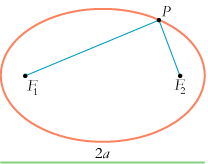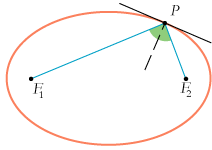Når man skal definere en ellipse, skal man til en start vælge to vilkårlige punkter F1 og F2 og et liniestykke, hvis længde betegnes 2a. Afstanden mellem F1 og F2 skal være mindre end 2a. Ellipsen består så af de punkter P i planen, hvis afstande fra F1 og F2 har summen 2a. De to blå liniestykker på figuren skal altså tilsammen være lig længden af det grønne liniestykke. F1 og F2 kaldes ellipsens brændpunkter, og de to blå liniestykker kaldes brændstråler. Man kalder a den halve storakse. Hvis man opfatter det sådan, at man har fastgjort enderne af en blå snor med længde 2a i brændpunkterne, og holder snoren stram med en blyantsspids i P, ja så kan man tegne ellipsen ved at flytte blyanten sådan, at snoren hele tiden er stram.

På figuren har vi tegnet tangenten til ellipsen i punktet P. Den punkterede linie er normalen til ellipsen i punktet P. Normalen står vinkelret på tangenten. Så har ellipsen den meget attraktive egenskab, at normalen halverer den grønne vinkel mellem brændstrålerne. Lad os nu tænke os, at ellipsen er spejlende på indersiden. Ifølge tilbagekastningsloven betyder det, at hvis man anbringer en punktformet lysgiver i F1, da vil alle de tilbagekastede lysstråler gå gennem F2. På den måde kan man få koncentreret en masse lys i et brændpunkt. Og det er naturligvis derfor, det hedder sådan.

Tallet e = F₁ F₂/2a kaldes ellipsens excentricitet. Tallet e ligger mellem 0 og 1. Når brændpunkterne ligger tæt ved hinanden i forhold til 2a, er e tæt ved 0, og ellipsen er tæt ved at være en cirkel. Når F₁ F₂ er næsten lige så stor som 2a, er e tæt ved 1 og ellipsen er meget fladtrykt. Tallet e er altså et mål for, hvor fladtrykt ellipsen er.

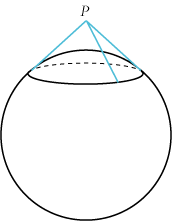Vi får om lidt brug for en ganske enkel iagttagelse: Lad os kigge på en kugle og et punkt P uden for kuglen. Gennem P går der en masse tangenter til kuglen, men længden af stykket fra P til røringspunktet er den samme, ligemeget hvilken tangent vi kigger på.

Ellipsen kan beskrives på en helt anden måde, som måske nok er mere naturlig end den, vi anvendte ovenfor. Vi vil nemlig bevise, at skæringskurven mellem en cylinder med cirkulært tværsnit og en skrå plan er en ellipse.

På figuren ser man den lodrette cylinder tegnet med sort og den røde snitplan. Den ovale skæringskurve er også tegnet rød. Beviset, for at det bliver en ellipse, begynder som en genial plan af Egon Olsen fra Olsen Banden: Vi skal bruge en gul ballon og en tung sort kugle af samme størrelse. De skal begge to have samme diameter som cylinderen. Kuglen putter vi ned i cylinderen ovenfra. Vi lader den falde, indtil den rører snitplanen i et punkt F2. Så holder vi ballonen neden under cylinderen, og lader den stige til vejrs indtil den stoppes af snitplanen, som den så berører i et punkt F1. Og så er det mærkværdigvis sådan, at snitkurven er en ellipse med brændpunkter F1 og F2. Det viser vi ved at betragte et vilkårligt punkt P på snitkurven. Vi skal vise, at summen af afstandene PF1 og PF2 er den samme, uanset hvor på snitkurven vi har valgt P. Vi tegner det lodrette liniestykke AB gennem P. A og B ligger på de to vandrette cirkler, som kuglerne rører cylinderen i. Så er PF1 = PB. Det følger af iagttagelsen ovenfor, PF1 og PB er jo begge tangenter til den gule ballon. På samme måde ses at PF2 = PA. Men så må PF1 + PF2 = AB, altså uafhængig af beliggenheden af P på snitkurven. Kurven er altså en ellipse med brændpunkter F1 og F2 og storakse lig med afstanden AB.

Resultatet illustreres på billedet nedenfor. Det er fra Herlev Sygehus. Cylinderen er en betonsøjle, og snitplanen er den plan, der indeholder Solen og den nederste kant af altanen.

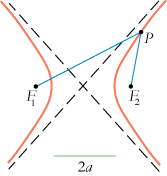
Definitionen af en hyperbel minder om ellipsedefinitionen: Man skal igen vælge to brændpunkter F₁ og F₂ og et grønt liniestykke med længden 2a. Afstanden mellem F₁ og F₂ skal denne gang være større end 2a. Hyperblen består så af de punkter P for hvilke forskellen mellem de to blå afstande PF₁ og PF₂ er 2a. Ligesom man kunne tegne ellipsen ved hjælp af en snor med længde 2a kan man tegne en hyperbel med en lynlås, hvor man har klippet et stykke af længde 2a af den ene side. (Det har man ellers sjældent brug for med lynlåse!) Hyperblen har to asymptoter, det er de punkterede linier. Dem nærmer hyperblen sig ubegrænset til, når man går langt væk. Nederst på siden er der et eksempel på naturligt forekommende hyperbler.

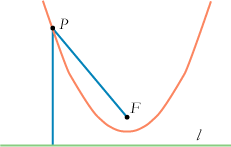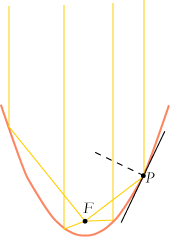Når man skal definere en parabel, skal man først vælger et brændpunkt F og en ledelinie l, den vandrette grønne linie på figuren. Parablen består så af de punkter P, der ligger lige langt fra P og l. De to blå liniestykker skal altså være lige store. Begge grene af parablen strækker sig uendeligt langt opad. Linien gennem F vinkelret på l kaldes parablens akse. Den er symmetriakse for parablen.

Ligesom ellipsen har parablen også en meget nyttig spejlingsegenskab. I et parabelpunkt P tegner vi tangenten og den punkterede normal. Normalen halverer så vinklen mellem PF og linien fra P og lodret opad, parallelt med aksen. Så hvis vi tænker os, at parablen er spejlende på indersiden, så vil en lysstråle fra F reflekteres lodret opad. Vi tænker os nu, at vi danner en flade, - en paraboloide - ved at dreje parablen om sin akse. Hvis paraboloiden er spejlende på indersiden, kan man lave en projektør ved at anbringe en lille lysgiver i brændpunktet. De reflekterede stråler vil da alle være parallelle med aksen. Hvis man omvendt retter paraboloidens akse mod en kommunikationssatellit, så vil signalerne koncentreres i brændpunktet.

Vi lægger nu et koordinatsystem ind, som det er vist på figuren. For at få et pænt resultat kalder vi afstanden mellem ledelinie og brændpunkt for p/2. Lad P med koordinaterne (x,y) være et punkt på parablen. Så er afstanden Pl fra P til l lig med y+p/4, og derfor fås, at

Ved at anvende pythagoras på den blå trekant fås, at

Men da (Pl)² = (PF)² vil

hvilket ved udregning giver parablens ligning

Denne ligning udtrykker betingelsen for, at et punkt med koordinater (x,y) ligger på parablen.

Vi får brug for to forberedende bemærkninger:

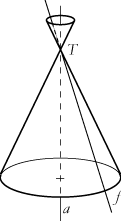Lad a og f være to linier, der skærer hinanden i et punkt T. Hvis man drejer linien f om a beskriver f en flade, der kaldes en kegleflade. Den strækker sig i det uendelige, men på figuren har vi skåret den af opad og nedad. Fladen består af linier gennem T. De kaldes frembringere, T kaldes keglefladens toppunkt og a kaldes dens akse. Vinklen v mellem en frembringer og aksen kaldes den halve toppunktsvinkel. Nedenfor skal vi fortælle hvilke kurver, der kan fremkomme, når man skærer keglefladen med en plan.

Vi får brug for en ganske enkel iagttagelse: Lad os kigge på en kugle og et punkt P uden for kuglen. Gennem P går der en masse tangenter til kuglen, men længden af stykket fra P til røringspunktet er den samme, ligemeget hvilken tangent vi kigger på.

Årsagen til at ellipsen, parablen og hyperblen hedder keglesnit er, at disse tre kurvetyper fås, når man skærer en kegleflade med en plan. Hvilken kurve man får afhænger af, hvor skrå snitplanen er. Lad u være vinklen mellem aksen og snitplanen. Vi starter med tilfældet u>v. Så skærer snitplanen alle frembringere på samme side af toppunktet.

På figuren er snitplanen rød. Den skærer keglefladen i den røde ovale kurve. Først vil vi så tvivl om, at den røde kurve er en ellipse: Sagen er jo den, at keglefladen krummer mest oppe i nærheden af toppunktet og mindre og mindre længere nedad. Man skulle derfor vente en ægformet kurve. Men det er altså alligevel en ellipse, og det findes der et vidunderligt argument for. Argumentet er først fundet af Germinal Dandelin i 1822, selv om resultatet var kendt allerede af Apollonius.

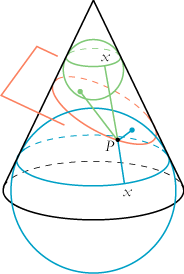
Vi har altså en kegleflade og en rød snitplan, der skærer keglen i en rød kurve. Så tager vi en lille grøn kuglerund ballon. Den putter vi ind øverst i keglen, og så puster vi den op, indtil den rører den røde plan i en enkelt punkt, det grønne punkt. Ballonen rører keglen indvendigt langs den vandrette, grønne cirkel. Så tager vi en stor, blå ballon. Den putter vi nedefra op i keglen, indtil den rører keglen langs en vandret blå cirkel. Og så lukker vi luft ud af den blå ballon, lige indtil den netop rører den røde plan i et enkelt punkt, det blå punkt. Lad så P være et vilkårligt punkt på den røde kurve. Vi forbinder P med det grønne og det røde punkt, og på frembringeren gennem P farver vi stykket fra P op til den grønne cirkel grønt og stykket fra P og ned til den blå cirkel farver vi blåt. Så følger det af iagttagelsen ovenfor, at de to grønne liniestykker er lige store og at de to blå liniestykker er lige store. Men så er summen af P´s afstande fra det grønne og det blå punkt lig med afstanden xx, altså konstant, uafhængigt af hvor på den røde kurve P ligger. Den røde kurve er altså en ellipse, hvis brændpunkter er det blå punkt og det grønne punkt, og hvis storakse er afstanden xx.

Kuglerne hedder Dandelins kugler.

Vi betragter nu tilfældet u=v. I det tilfælde skærer snitplanen alle frembringere på nær én, som er parallel med snitplanen. Situationen er vist her på figuren:

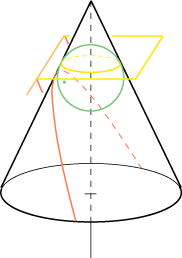
Snitkurven er rød, og for at vise at det er en parabel, skal vi have fat i brændpunktet og ledelinien. Brændpunktet findes ved hjælp af en dandelinkugle, som er grøn. Den rører keglen på indersiden langs den vandrette gule cirkel, og den rører snitplanen i et enkelt punkt, det grønne punkt. Den gule plan skærer den røde plan i den orange linie. Under udfoldelse af nogen snedighed kan man så vise, at snitkurven er en parabel med det grønne punkt som brændpunkt og med den orange linie som ledelinie.

Til sidst betragter vi det tilfælde, hvor u<v. I det tilfælde skærer snitplanen både den øverste og den nederste del af keglen, og man kan ved hjælp af Dandelins kugler bevise, at snitkurven bliver en hyperbel.

Lad os i rummet betragte et keglesnit K og et punkt T, der ikke ligger i keglesnittets plan. Den flade, der består af de linier gennem T, der skærer K, kaldes også en kegleflade. K kaldes ledekurven og T kaldes toppunktet. Man kan bevise, at også sådan en flade skæres af en plan i et keglesnit.

For at se et eksempel på, at hyperbler forekommer i naturen, stikker vi en pind i jorden. Den kaldes en gnomon. Hvordan mon skyggen af toppen af pinden så bevæger sig i løbet af en dag?

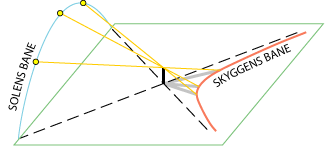
Ja, skyggen starter jo teoretisk langt væk modsat solopgangen. Den er kortest midt på dagen, og endelig slutter den langt væk modsat solnedgangen. Lad os kigge på den kegleflade, der har solens bane i det pågældende døgn som ledekurve og toppen af pinden som toppunkt. Så er skyggens banekurve skæringskurve mellem keglefladen og den plane, grønne jordoverflade. Så skyggen beskriver en hyperbelgren. Med mindre man er oppe i Grønlands midnatssol, for der bliver det en ellipse.

Hvis du støder på et ord, hvis betydning du ikke kender, så søg på ordet.