|
Forside
Søgning
Liste |  |
Om Nicole Oresmes arbejder
1. Kinematik
Omkring 1350 skete der et bemærkelsesværdigt fremskridt i den måde, man beskriver en partikels bevægelse på. Ideen skyldes Nicole Oresme. Der er tale om en forløber for koordinatsystemet, og man aner også en tidlig spire til differential- og integralregning. Den grundlæggende ide er følgende: Vi betragter en partikel, der bevæger sig i tidsintervallet fra 0 til T. Endvidere tænker vi os, at vi til hvert tidspunkt t kender partiklens fart v(t). Oresme tegner så et liniestykke (det kaldes longitudo), der afbilder tidsintervallet fra 0 til T. Til ethvert tidspunkt t tegnes dernæst et lodret liniestykke opad fra punktet t på longitudo. Det kaldes latitudo. Dets længde skal være v(t). Disse lodrette liniestykker udfylder så et område i planen, som Oresme kalder bevægelsens konfiguration. Oresme benytter konfigurationen til at bestemme den vejlængde s, som partiklen gennemløber i tidsintervallet fra 0 til T. Vi illustrerer her fremgangsmåden med tre eksempler:
Eksempel 1
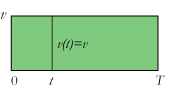
Her betragter vi en jævn bevægelse med hastighed v. Alle latitudo liniestykker ender så i samme højde, og bevægelsens konfiguration bliver det grønne rektangel. Den gennemløbne vejlængde s er naturligvis v·T, så s er altså lig med arealet af det grønne rektangel.
Eksempel 2
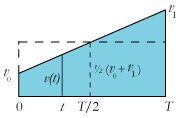
I dette tilfælde tænker vi os at partiklen starter med hastighed v0 og at den har konstant acceleration (se 1335 Heytesbury), så den ender med hastigheden v1. Bevægelsens konfiguration bliver så den blå firkant på figuren. Den øvre begrænsning af konfigurationen er et liniestykke, fordi der til vilkårlige lige store tidsintervaller svarer lige store hastighedsforøgelser. Den tilbagelagte vejlængde s bliver så (se 1330 Mertonskolen) s=½T(v0 + v1). Den blå firkants areal er lig med arealet af rektanglet på figuren, altså T·½(v0 + v1). Igen er vejlængden altså lig med konfigurationens areal. Og sådan er det faktisk hver gang, som vi skal se i det tredie eksempel.
Eksempel 3
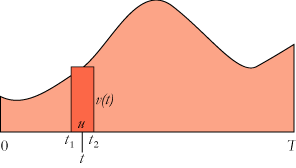
Til sidst lader vi partiklen bevæge sig frit i det givne tidsinterval. Bevægelsens konfiguration kan så f.eks. se ud som det lyserøde område på figuren ovenfor. Vi kigger nu først på et tilfældigt, men kort tidsinterval fra tidspunktet t1 til tidspunktet t2. Tidsintervallets længde er u=t2 - t1. Hvor langt mon partiklen har bevæget sig i dette tidsinterval? Hvis t er f.eks. midt i tidsintervallet, og hvis u er lille nok, kan vi med god tilnærmelse regne med, at hastigheden er konstant lig med v(t) i det betragtede interval. Den vejlængde, som partiklen bevæger sig fra kl. t1 til kl. t2 er så u·v(t), altså arealet af det mørkerøde rektangel. Nu tænker vi os hele intervallet fra 0 til T dækket af sådanne mørkerøde rektangler:
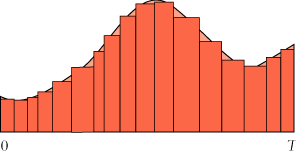
Så vil den vejlængde s, som partiklen gennemløber i tidsintervallet fra 0 til T være lig med det samlede areal af de mørkerøde rektangler, og hvis de alle er smalle nok kan vi regne med, at det er det samme som det lyserøde areal. Altså:
Den gennemløbne vejlængde er lig med arealet af bevægelsens konfiguration
2. Oresmes aristoteleskritik
Mens ovenstående sætning skyldes Oresme, er de betragtninger, der leder frem til den, ikke hans. Vi synes nu det er svært at forestille sig, at Oresme kan være nået frem til den indholdsrige sætning uden overvejelser af den citerede art.
Vi slutter omtalen af Oresme med et eksempel fra hans kritik af Aristoteles. Den udtalelse af Aristoteles, som det drejer sig om er følgende: "Når et legeme bevæger sig i uendelig lang tid vil den tilbagelagte vejlængde også være uendelig lang."
Oresme viser, at denne påstand er forkert med følgende eksempel. Et legeme bevæger sig i det første
døgn med hastighed v, i det andet døgn med hastighed v/2, i det tredie døgn med
hastighed v/4 o.s.v. idet vi for hvert døgn halverer hastigheden. Hvis vi bruger den vejlængde,
som legemet gennemløber i det første døgn som enhed er de gennemløbne afstande 1, 1/2, 1/4, 1/8, ... .

På figuren har vi tegnet et liniestykke af længden 2 og ovenover har vi afsat de afstande, som legemet tilbagelægger i de første fire døgn. Pointen er nu, at legemet i hvert døgn kommer halvvejs hen til enden af liniestykket. Selv om legemet altså bevæger sig uendelig længe, når det aldrig mere end 2 enheder væk fra startpunktet.
3. Om Jordens bevægelse
Hvis Jorden bevægede sig, ville der hele tiden være en frygtelig blæst på Jorden. Det er et af
de argumenter, der blev anvendt mod Jordens bevægelse. Oreme gjorde opmærksom på, at argumentet
mister sin betydning, hvis man blot antager, at den nederste del af lufthavet følges med Jorden i
dens bevægelse. Oresme afviser også andre argumenter mod Jordens bevægelse, men han ender alligevel med
trods alt at erklære, at han selv ikke tror på, at Jorden bevæger sig!
| Hvis du støder på et ord, hvis betydning du ikke kender, så søg på ordet. |