Forside Søgning Liste

Archimedes vidste god besked om tyngdepunkter. Det kan man bl.a. se i hans behandling af svømmende legemers ligevægt. Hans grundlæggende skrift om tyngdepunkter er imidlertid ikke bevaret, men der er bevaret flere arbejder, der handler om tyngdepunkter, bl.a. altså hans arbejde om svømmende legemers ligevægt. Se nærmere i biografien. Pappus, der levede i 300-tallet, altså 600 år efter Archimedes, formulerede imidlertid en præcis definition af begrebet tyngdepunkt, og han kan have været inspireret af Archimedes. Nedenfor beskriver vi Pappos definition af tyngdepunkt. Vores beskrivelse er tæt på Pappus egen. Vi sætter meget pris på det afgørende argument.

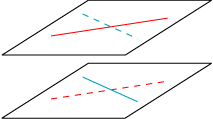Vi får brug for en egenskab ved linier i rummet. Vi betragter to linier i rummet, en rød og en blå, og forudsætter, at de ikke har noget punkt fælles. Så findes der to parallelle planer, der indeholder hver sin af de to linier. Den punkterede røde linie på figuren fås ved, at man parallelforskyder en kopi af den røde linie, til den skærer den blå. Og omvendt. De skærende par af linier bestemmer så to parallelle planer, der indeholder henholdsvis den røde og den blå linie.

Figuren til højre viser et rumligt legeme, der i et punkt A er ophængt i en snor, og som er faldet til ro, så der er ligevægt. A kaldes ophængningspunktet, og den lodrette linie l, der indeholder snoren, kaldes en ophængningslinie. Til højre har vi det samme legeme, men vi har anvendt et andet ophængningspunkt B og får en anden ophængningslinie m. På figuren ligner legemet sig selv, men normalt vil det se anderledes ud, når det hænger i et andet punkt. Figuren er rumlig, så man kan ikke på figuren se, om de to ophængningslinier skærer hinanden eller ej. Vi vil imidlertid bevise, at to ophængningslinier altid skærer hinanden.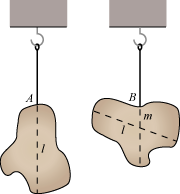

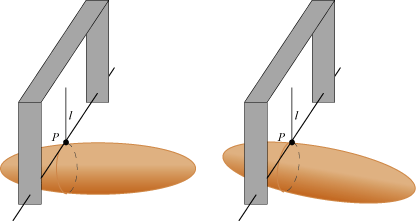-Af hensyn til overskueligheden på figuren nedenfor er vi nødt til at tegne et aflangt legeme, der hænger i en snor. På figuren længst til venstre tænker vi os først, at legemet er ophængt i P med ophængningslinie l, og at det er i ligevægt. Legemet må åbenbart have noget tungt inden i sig ude til venstre. Så limer vi den sorte vandrette aksel fast ovenpå legemet i punktet P. Akslen kan dreje sig i den grå holder, og vi fjerner snoren l. Så er legemet en vægtstang i ligevægt. For hvis legemet vippede lidt, som på figuren til højre, ville det allerede være vippet, da det hang i snoren.

Vi antager nu forsøgsvis, at der findes et legeme med to ophængningslinier l og m, der ikke skærer hinanden; og så vil vi se, hvad det fører til. Vi kalder ophængningspunkterne P og Q. Da linierne ikke skærer hinanden, ligger de i to parallelle planer α og β. l, m, P, Q, α og β er fast forbundet med legemet, de flytter med, hvis man flytter legemet. De to planer deler legemet i tre dele, som vi kalder A, B og C.

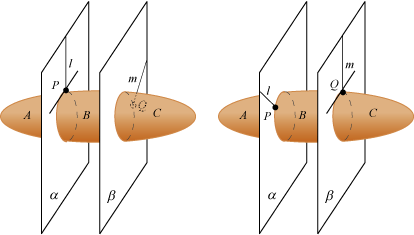
Vi hænger nu legemet op i en snor med ophængningspunkt P og ophængningslinie l. Da l er lodret, er planerne α og β også lodrette. Vi kan som ovenfor opfatte legemet som en vægtstang, der kan dreje sig om den vandrette linie i α gennem P. Der er ligevægt, så legemet A til venstre afbalancerer præcis legemerne B og C til højre. På figuren til højre viser vi, hvordan det ser ud, når vi i stedet hænger legemet op i ligevægt i ophængningspunktet Q. Legemet har drejet sig på en eller anden måde, men α og β er igen lodrette. Vi opfatter nu igen legemet som en vægtstang, denne gang med den vandrette linie i β gennem Q som omdrejningsakse. Pointen er nu, at selv om legemet har drejet sig på en ukendt måde, så har hvert enkelt punkt af legemet beholdt sin afstand fra α og β. Men så kan der umuligt være ligevægt til højre. For i forhold til ophængningspunktet er alle tre legemer A, B og C flyttet en tak til venstre, og så må venstre side af vægtstangen dreje nedad. Dette er i modstrid med, at der også er ligevægt på figuren til højre. Vores antagelse førte altså til en selvmodsigelse, derfor må den være forkert. Resultatet er, at vi har vist, at to ophængningslinier altid skærer hinanden. Et bevis af denne type, hvor man antager noget, som viser sig at være forkert, kaldes et indirekte bevis.

Så nu står vi og kigger på et legeme og alle dets uendelig mange ophængningslinier. To og to skærer de hianden, det må vel give et mylder af skæringspunkter!? Nej, for nu vil vi bevise, at de allesammen skærer hinanden i et og samme punkt:

For ethvert legeme findes der et punkt, der ligger på alle ophængningslinier

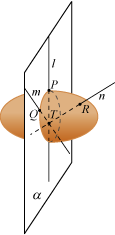
Sådan beviser man påstanden: Lad l og m være to ophængningslinier. De skærer hinanden i et punkt T og ligger i en plan α. Vi skal vise, at alle andre ophængningslinier også går gennem T. Først og vigtigst vælger vi en ophængningslinie n med et ophængningspunkt R, der ikke ligger i planen α. Vi ved, at n skærer både l og m, men det kan den kun komme til i punktet T. Så nu har vi vist, at 99% af alle ophængningslinier går gennem T. Vi mangler kun de ophængningslinier, der ligger i planen α. Men sådan en linie skærer både l, m og n, og det kan den kun komme til, hvis den går gennem T.

T kaldes legemets tyngdepunkt. Det spiller en rolle i mange sammenhænge, se f.eks. 1586 Stevin.

Det sidste bevis gælder ikke, hvis legemet er en plan figur. (Det kan man ikke se bort fra. Også plane figurers tyngdepunkter er vigtige.) Resultatet er rigtigt alligevel. Det kan man se ved et indirekte bevis, omtrent som ovenfor

Vi finder det imponerende, at Pappos, eller hvem det nu kan være, allerede i 300-tallet kunne gennemføre en sådan abstrakt analyse og nå frem til en præcis definition af begrebet tyngdepunkt. Det er et lyspunkt i en periode, hvor det ellers er småt med fremskridt i fysikken.

Hvis du støder på et ord, hvis betydning du ikke kender, så søg på ordet.