Forside Søgning Liste

Et af hovedproblemerne i astronomien i oldtiden var beregning af planetbaner. Det er ikke simpelt. Figuren nedenfor viser, hvordan Mars bevægede sig mellem stjernerne i en bestemt periode på ca 2 år.

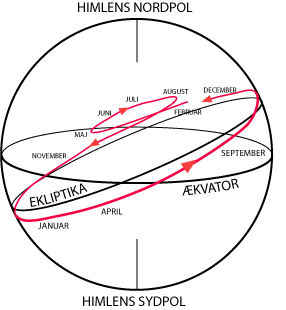
Problemet er at forklare og beregne sløjfen, som man her ser på bagsiden af himmelkuglen. Den viste del af marsbanen gennemløbes på lidt under 2 år. Men den gentages ikke nøjagtigt i den følgende 2-årsperiode. Der er en sløjfe ca hvert andet år, men sløjfen kan f.eks. være S-formet næste gang. Og den vil være placeret på et andet sted på himlen, dog i nærheden af Ekliptika.

Ved beregning af planetbanerne benyttede Ptolemæus epicykler. For at få tilstrækkelig god overensstemmelse med observationerne måtte Ptolmæus benytte et meget kompliceret system af epicykler. Her vil vi nøjes med at beskrive den grundlæggende ide, som giver en beskrivelse af planetbanerne under forudsætning af at planeterne udfører jævne cirkelbevægelser i Ekliptikas plan og med centrum i Solen, som går rundt om Jorden. Der er altså tale om et geocentrisk system. Under disse forudsætninger vil planeterne set fra Jorden bevæge sig i epicykelformede baner.

Vi starter med at beskrive banebevægelsen for Mars i 1708 - 1709, hvor den retrograde bevægelse fandt sted i perioden november til februar. Under de nævnte forudsætninger flyttes den ovenfor viste marsbane ned på Ekliptika. Det drejer sig altså om at beskrive Mars' bevægelse på Ekliptika, herunder den korte periode med retrograd bevægelse:

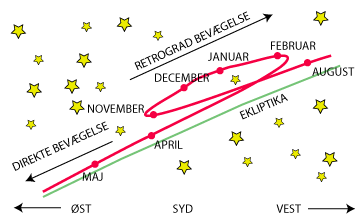
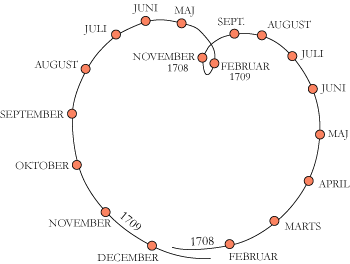
Læg mærke til, at den retrograde bevægelse finder sted samtidig på begge figurer. Vi vil ikke gå nærmere ind på Ptolemæus teori her, men hvis vi går ud fra ovennævnte forudsætning, og sætter omløbstiden for Mars til 2 år (i stedet for 1,8 år), så vil Mars faktisk i et geocentrisk system bevæge sig som vist på animationen nedenfor. Jorden er i hvile, Solen bevæger sig i en cirkel med centrum i Jorden, og Mars bevæger sig i en cirkel med et bevægeligt centrum i Solen.

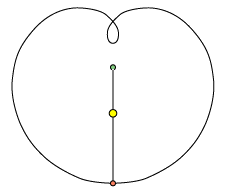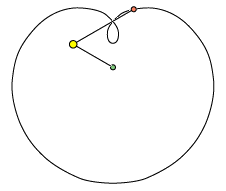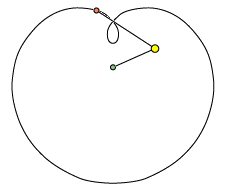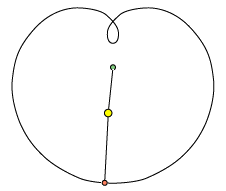
Læg mærke til at forholdet mellem de to stanglængder er lig med forholdet mellem Jordens og Mars afstand til Solen. Epicykelteorien kunne altså godt danne udgangspunkt for bestemmelse af afstandene i solsystemet målt med jordbaneradius som enhed, men det var der vist ingen, der tænkte på dengang.

Man kan spørge om Ptolemæus' epicykelmodel er en korrekt beskrivelse af planetbevægelsen. Svaret er, at så længe der er tale om de relative bevægelser af de tre himmellegemer, er epicykelmodellen korrekt. Epicykelmodellen svigter først, når man begynder at interessere sig for planeternes bevægelser i forhold til stjernehimmelen. Da man fandt aberrationen (se Bradley) og senere de første parallakser (se Bessel) blev man klar over, at Jorden bevæger sig om Solen. I epicykelmodellen svarer det til at beholde stængernes bevægelse i forhold til hinanden, men fastholde Solen i stedet for Jorden.

Jupiter udviser en mere kompliceret epicykelbevægelse end Mars. Hvor marsbanen omtrent har én sløjfe pr marsomløb har Jupiter ca 11 sløjfer pr jupiterår. Figuren nedenfor viser en epicykelbeskrivelse af Jupiters bane fra 1708 til 1720:

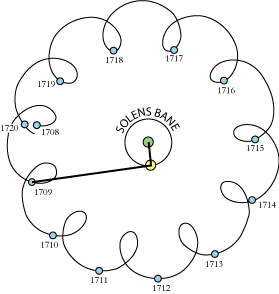
Her er den lange stang 5 gange så lang som den korte, i overensstemmelse med at radius i Jupiters bane om Solen er 5 gange så lang som jordbanens radius. Den korte stang skal dreje sig ca 12 gange så hurtigt som den lange.

Det er jo en mystisk bane, Jupiter gennemløber i verdensrummet under et omløb om Jorden. Men det er som nævnt rigtigt nok i den forstand, at trekanten Jord, Sol, Jupiter har den rigtige form under hele tegningen af epicyklen. Men selv i gamle dage må de da have overvejet, hvor meget simplere det hele ville være, hvis man fastholdt Solen i stedet for Jorden!

Vi afslutter denne omtale af Ptolemæus arbejde med en omtale af asteroiden Ceres. Ptolemæus kendte ikke Ceres. Vi vælger den her, fordi dens omløbstid og afstand fra Solen er bekvemme ved udarbejdelsen af en animation, der illustrerer problemerne. Asteroiderne er små planeter, deres baner ligger mellem banen for Mars og Jupiters bane. Vi regner med følgende data for Ceres: Omløbstiden er 5 år, banen er cirkulær med radius 2,9 jordbaneradier og baneplanen er Ekliptikas plan. Vi vil beskrive bevægelserne af Solen, Jorden og Ceres, både heliocentrisk og geocentrisk. "Heliocentrisk", - med centrum i Solen, "Helios", og "geocentrisk" - med centrum i Jorden, "Geus".

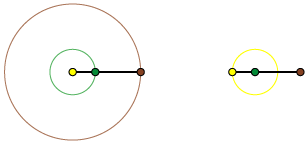
Til en start tænker vi os, at de tre himmellegemer Solen (gul), Jorden (grøn) og Ceres (brun) ligger på en ret linie, der peger på en stjerne S langt ude til højre. Den heliocentriske bevægelse foregår, som det er vist til venstre på animationen nedenfor. Hver gang Ceres drejer en gang rundt om Solen drejer Jorden 5 gange rundt om Solen. Til højre viser vi, hvordan bevægelsen vil se ud, hvis vi vælger samme startposition (incl S) som før, men fastholder Jorden i stedet for Solen. Vi forudsætter også, at de to sorte stænger drejer sig med samme vinkelhastigheder og omløbsretninger som til venstre.

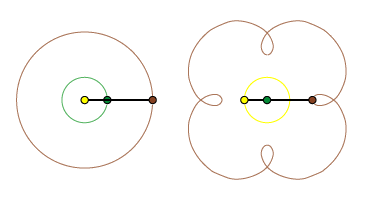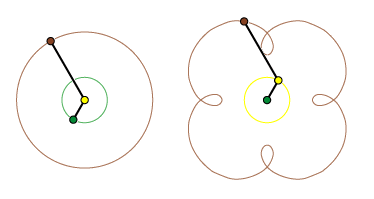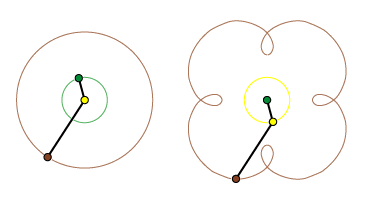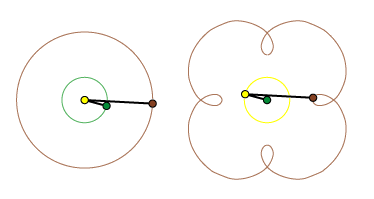
Bevægelsen af Ceres foregår nu på en epicykloide. Læg mærke til, at hver gang Jorden til venstre overhaler Ceres indenom, da udfører Ceres til højre en kortvarig retrograd bevægelse. Læg også mærke til, at de to trekanter Jord-Sol-Ceres hele tiden er kongruente (ens), også i deres orientering i forhold til S. På denne baggrund kan man forstå, at Ptolemæus fik fornuftige resultater ved at benytte epicykelformede planetbaner. Den afgørende forskel på de to modeller er, at i den geocentriske model er sigtelinien til stjernen S en fast linie i verdensrummet, mens sigtelinien fra Jorden til S i den heliocentriske model til venstre vipper lidt frem og tilbage i årets løb på grund af Jordens bevægelse. Denne mikroskopiske bevægelse kaldes stjernens årlige parallakse. Den blev først målt af Bessel i 1838. Det viser, at den heliocentriske model er den korrekte.

Sagen kompliceres af, at planetbanerne er svagt aflange ellipsebaner, at Solen ikke er i centrum, at planeterne ikke går lige hurtigt hele tiden, og at baneplanerne ikke er sammenfaldende. Af disse grunde måtte Ptolemæus indføre en række korrektioner af epicykelbanerne. Disse korrektioner var så velvalgte, at den opnåede nøjagtighed var nede på et par bueminutter, dvs en femtendedel af Månenes vinkeldiameter.

Hvis du støder på et ord, hvis betydning du ikke kender, så søg på ordet.