Forside Søgning Liste

Når man skal konstruere et stjernekort, har man det samme problem, som når man skal tegne et plant kort over en del af den krumme Jord: Ingen del af en kugleflade kan afbildes på en plan, uden at der sker en ændring af afstandsforholdene. Man har derfor udtænkt en række kortprojektioner, som man bruger, når man skal tegne et kort. Vi skal her beskrive en af disse projektioner. Den kaldes den stereografiske projektion, og den er første gang beskrevet af Ptolemæus.

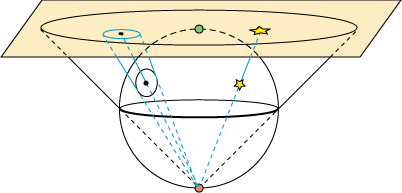
På figuren viser vi himmelkuglen med himlens nordpol øverst. Det er det grønne punkt. Den plan, som vi vil tegne stjernekortet på, er den lysegule plan. Den er tangentplan til himmelkuglen, og røringspunktet er netop himlens nordpol. Vi ser bort fra den daglige omdrejning og tænker os, at stjernerne har faste positioner på himmelkuglen. Vi vælger så en tilfældig stjerne på himmelkuglen, og skal bestemme, hvor på stjernekortet denne stjerne skal afbildes. Vi får så brug for himlens sydpol, dvs det nederste punkt af himmelkuglen. Det er det røde punkt. Så tegner vi en linie fra det røde punkt og op gennem stjernen, og der hvor denne linie skærer den lysegule plan, skal stjernen tegnes ind på stjernekortet. På denne måde konstrueres hele stjernekortet. Himlens ækvator kan tegnes ind på stjernekortet ligesom stjernerne: Man tegner linier fra sydpolen, der skærer himlens ækvator. Skæringspunkterne med stjernekortet udgør så ækvator på stjernekortet. Det er den sorte ellipse oppe i den lysegule plan - i virkeligheden er det naturligvis en cirkel. Hvis man afbilder en kugle på en plan på denne måde, siger man, at man har udført en stereografisk projektion.

Den stereografiske projektion har både fordele og ulemper. Det er en ulempe, at målestoksforholdet bliver større og større, når man bevæger sig væk fra himlens nordpol. Men den stereografiske projektion har en afgørende fordel: Den er vinkeltro. Det medfører, at hvis et stjernebillede ikke har alt for stor udstrækning, så gengives det med korrekt facon, når man konstruerer stjernekortet.

Vi tænker os nu, at der er en iagttager, der på et bestemt tidspunkt, tegner stjernekortet. Den iagttager har et zenitpunkt lige oppe over hovedet. Det er det sorte punkt på himmelkuglen. Det afbilder iagttageren så op på stjernekortet, sådan som det er vist på figuren. Nede på himmelkuglen er der også tegnet en lille sort cirkel. Den består af de punkter, der ligger 10° fra zenit, dvs dem, der ligger 80° over horisonten. Denne højdekurve tegnes også ind på stjernekortet, det er den blå ellipse på figuren. På den måde kan man naturligvis tegne så mange højdekurver, som man vil. 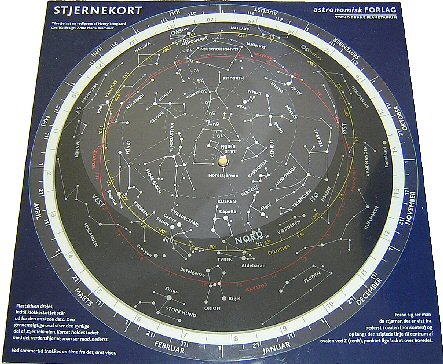Men der er et problem: På grund af Jordens daglige rotation vil zenit bevæge sig en gang rundt på en cirkel med centrum i himlens nordpol, og højdekurverne vil følge med. Det er derfor smart at tegne zenit og højdekurverne og himlens nordpol på et særligt stykke papir, som kan dreje sig om nordpolen i forhold til stjernekortet. Denne ide bruges i populære stjernekort nutildags, se figuren nedenfor, og den er også den grundlæggende ide i konstruktionen af et astrolabium.

Den stereografiske projektion anvendes også ved konstruktion af kort over Jorden. Himmelkuglen skal så erstattes med Jorden. Den stereografiske projektion er især velegnet, når man skal kortlægge de arktiske egne.

Ptolemæus´ kartografi

Ptolemæus´ kartografiske arbejder er gået tabt. Billedet ovenfor viser et kort fra en afskrift fra 1427 af et ptolemæushåndskrift. Kortet er dog ændret foroven til venstre, fordi Grønland er blevet tilføjet.

Hvis du støder på et ord, hvis betydning du ikke kender, så søg på ordet.