Forside Søgning Liste

Simon Stevins vigtigste resultat er en ligevægtsbetingelse for legemer på et skråplan. Argumentet er elegant og enkelt. Stevins originale illustration til det findes i biografien. Ligevægtsbetingelsen var tidligere fundet af Jordanus Nemorarius, men Stevins argumentation er langt mere tilfredsstillende. Vi ved ikke, om Stevin kendte Nemorarius´ arbejde.

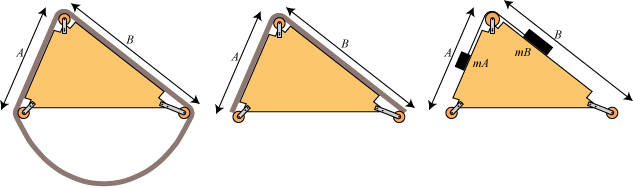
Vi kigger altså på skråplanet på figuren, og så tager vi et ringformet reb. Rebet skal være ens hele vejen rundt, det skal være tungt, det skal være glat, og det skal kunne bøjes uden modstand. Lad os sige, at hver centimeter af rebet vejer m gram. Dette reb hænger vi rundt om skråplanet, som det er vist på figuren til venstre. For at sikre os, at det kan glide rundt om skråplanets spidser uden modstand, sætter vi de viste 3 små trisser på. Til en start sørger vi for, at rebet ikke bevæger sig. Skråplanet er jo ikke lige skråt på begge sider; kunne det få rebet til at starte en bevægelse til den ene side? Lad os tænke os, at rebet startede med at bevæge sig den ene vej rundt. Så kunne vi bremse det, til det stod stille, og derved få nogen energi til rådighed. Og det vel at mærke uden at der er sket nogen ændring i systemet. Så hvis vi gav slip igen, ville det gå i gang igen. På den måde ville vi have en evighedsmaskine, som kunne udføre et arbejde, og det er umuligt. På figuren til venstre er der altså ligevægt.

Den del af rebet, der er længere nede end skråplanets underside, hænger i en symmetrisk bue. Den trækker derfor lige meget i skråplanets retning i begge sider. Derfor vil ligevægten ikke blive forstyrret, hvis man fjerner den del af rebet. Der er altså også ligevægt på figuren i midten. Den del af rebet, der nu er til venstre, vejer mA gram. Det kan ikke gøre nogen forskel, at man samler denne vægt i et legeme, som det er vist på figuren til højre, hvor den tilsvarende ændring af skråplanets højre side også er foretaget. Ligevægtsbetingelsen for en situation som den til højre, er altså, at forholdet mellem vægtene er lig med forholdet mellem skråplanernes længder.

Alle fysikkens resultater ville være blevet fundet alligevel, selv om den første opdager var død, lige før han fandt på det. Men ovenstående argument af Stevin er enestående. Vi er ikke sikre på, at det ville være blevet fundet, hvis ikke Stevin havde fundet det. Som vi skal forklare, er Stevins resultat en følge af reglen om kræfternes parallellogram.

Aristoteles hævdede, at et tungt legeme falder hurtigere end et let. Stevin viste før Galilei ved et forsøg, at Aristoteles havde uret. Vi citerer Stevin:

"Eksperimentet imod Aristoteles er dette: Lad os tage to blykugler, hvor den ene vejer 10 gange så meget som den anden, og lad dem falde samtidig fra 30 fods højde [10 meter] ned på en plade eller noget andet, som giver en tydelig lyd. Så vil det vise sig, at den lette ikke bruger 10 gange så lang tid som den tunge, men at de falder så samtidigt på pladen, at man kun hører én lyd."

En af vores kilder siger også, at Stevin havde "en intuitiv forståelse af kræfternes parallellogram". Det skriver vi om i en linie om Stevin og kræfternes parallellogram.

Hvis du støder på et ord, hvis betydning du ikke kender, så søg på ordet.