|
Forside
Søgning
Liste |  |
Simon Stevins arbejder med hydrostatik, dvs. ligevægt i væsker
1. Indledning
Stevins arbejder med hydrostatik ligger i fortsættelse af Archimedes´ arbejder med samme emne. Men medens Archimedes mest arbejdede som en matematiker ville gøre, så tager Stevin udgangspunkt i den fysiske verden, han laver eksperimenter. Dette var dog ikke til hinder for, at hans tankegang kunne være meget elegant. Det er der beskrevet et eksempel på under hans arbejde med skråplanet, og her kommer flere eksempler. Archimedes´ arbejder var ikke gået tabt, men forelå i afskrifter. Vi ved imidlertid ikke, om Stevin kendte dem. I alle tilfælde begynder Stevin forfra med at beskrive grundlaget for hydrostatikken, dvs. læren om væsker i ligevægt.
2. Svømmende legemers ligevægt
Det er en fundamental egenskab ved væsker, at hvis man kigger på en væskemængde i hvile, f.eks.
noget vand i en beholder, så vil selv den mindste påvirkning udefra skabe bevægelse i væsken. Min
fysiklærer i mellemskolen forklarede det på den måde, at man kan trække et slagskib over Atlanterhavet
i en sytråd, hvis det er stille vejr - og hvis man har tid nok.
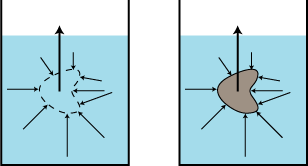
På figuren ovenfor til venstre har vi en beholder med vand i hvile. Vi tænker os nu en bestemt vandmængde afgrænset, som det er vist punkteret. Vandet i omgivelserne trykker fra alle sider på vores vandmængde, sådan som de små pile viser. Resultatet af alle disse små tryk må være en opadrettet kraft, den store pil, der netop kan bære vægten af vores vandmængde. Ethvert andet resultat vil jo få væsken til at bevæge sig. Den samlede opdrift på vores væskemængde er altså lig med væskemængdens vægt. Her kommer så et af Stevins elegante argumenter. Lad os tænke os, at den begrænsende punkterede overflade pludselig størknede til et tyndt lag af is. De omkringliggende vandpartikler ville så trykke ligesom før, og det vil de også gøre, hvis vi erstatter vores vandmængde med et fast legeme af samme form, men med vilkårlig vægt. Opdriften vil derfor være den samme, altså af samme størrelse som den fortrængte mængde vand. På den måde genfandt Stevin følgende resultat af Archimedes:
| Når et legeme nedsænkes helt i en væske, får det en opdrift, der er lig med vægten af den fortrængte væskemængde. Legemets vægt bliver altså formindsket med vægten af den fortrængte væskemængde. |
Stevin udvidede kendskabet til hydrostatik med følgende nye resultat:
| Hvis et legeme svømmer i en væskeoverflade og fortrænger sin egen masse i væske, da er der ligevægt, når legemets tyngdepunkt og den fortrængte væskemængdes tyngdepunkt ligger på samme lodrette linie. |
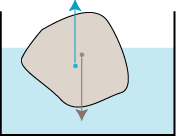
På figuren viser vi et svømmende legeme. Det er påvirket af to kræfter: Den brune tyngdekraft, der virker nedad i legemets tyngdepunkt, og den blå opdrift, der virker opad i den fortrængte vædskemængdes tyngdepunkt. Hvis de to tyngdepunkter ligger på samme lodrette linie er der ligevægt. Men hvis de, som på figuren, ligger på forskellige lodrette linier, vil de ifølge vægtstangsreglen dreje legemet væk fra den viste stilling; der er altså ikke ligevægt
Men, for der er et men: Hvis legemets tyngdepunkt ligger lodret under den fortrængte væskemængdes tyngdepunkt, da er der stabil ligevægt. Det betyder, at selv om man giver legemet et lille skub, så vender det selv tilbage til ligevægtsstillingen. Ved at lægge ballast i bunden af et skib kan man flytte skibets tyngdepunkt ned under den fortrængte vandmængdes tyngdepunkt og dermed opnå en stabil ligevægt. En ligevægtsstilling kaldes ustabil, hvis selv det mindste skub kan få legemet til at dreje til en anden ligevægtsstilling.
Hvis legemets tyngdepunkt ligger over den fortrængte væskemængdes tyngdepunkt, da kan ligevægten være
stabil, men den kan også være ustabil. Det kommer an på, hvordan de to tyngdepunkter placerer sig i
forhold til hinanden, hvis man vipper lidt med legemet. Vi illustrerer forholdet med to eksempler:
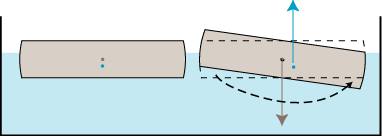
Vi starter med at betragte en lang, tynd planke af træ, der flyder på vand. Figuren viser til venstre tværsnittet midt i
planken.
De korte sider er cirkelbuer med centrum i tyngdepunktet. Planken har samme tværsnit hele vejen igennem.
Legemets tyngdepunkt er brunt, det ligger midt i tværsnittet. Den fortrængte
vandmængdes tyngdepunkt er blåt, det ligger midt i den fortrængte vandmængde. Da de to punkter ligger
på samme lodrette linie, er der ligevægt. Nu drejer vi legemet lidt om tyngdepunktet, sådan som det
er vist til højre. På grund af de buede kanter er det let at indse, at
den fortrængte vandmængde er den samme som før drejningen. Ved denne drejning flytter legemets tyngdepunkt
sig ikke. Men det gør den fortrængte vandmængdes tyngdepunkt. Den fortrængte vandmængdes
form er nemlig ændret, den er blevet tyndere til venstre og tykkere til højre. Derfor ligger det blå
tyngdepunkt, dvs. den fortrængte vandmængdes tyngdepunkt, et stykke til højre for det brune. Det blå tyngdepunkt
på figuren er placeret på baggrund af en omhyggelig konstruktion. Nu bruger vi
så vægtstangsreglen, idet vi tænker os, at legemets tyngdepunkt er omdrejningspunkt. Så er momentet
for tyngdekraften nul, og da vandtrykket opad virker i det blå punkt, ser vi, at vandtrykket vil dreje
legemet tilbage mod ligevægtsstillingen. Til
venstre er legemet altså i en stabil ligevægtsstilling.
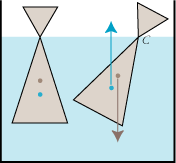
Derefter vil vi beskrive en situation, hvor der er ustabil ligevægt. Vi benytter en lang planke af træ, der flyder på vand. Men denne gang har legemet det mystiske tværsnit, der er vist på figuren. Den øverste trekants størrelse er valgt sådan, at legemets vægt er lig vægten af den vandmængde, som den nederste trekant fortrænger. Tyngdepunkterne for legemet (brunt) og for den fortrængte vandmængde (blåt) er igen indtegnet. De ligger på den lodrette midterlinie, og man ser som før, at der er ligevægt med legemets tyngdepunkt over vandets. Nu vil vi undersøge, om ligevægten er stabil. Vi drejer lidt om det punkt C, der ligger i vandoverfladen. Pointen er nu, at under drejningen bevarer den fortrængte vandmængde sin form. Derfor følger begge tyngdepunkter med under drejningen, sådan som det er vist på figuren. Vi opfatter nu legemet som en vægtstang med omdrejningspunkt C. Så har opdriften større arm end tyngden, og derfor er resultatet, at legemet selv drejer væk fra den oprindelige ligevægtsstilling. Ligevægten til venstre er derfor ustabil og faktisk ikke realiserbar.
Ligevægtsstillingen er ikke altid entydigt bestemt. F.eks. kan en terning af træ flyde i vand med et eller med et andet hjørne længst nede. Studiet af ligevægtsstillingerne er kompliceret.
3. Trykfordelingen i en væske
Den tankegang, der benyttedes i det foregående argument, benyttes igen i Stevins redegørelse for
væsker i forbundne kar:
 |
På figuren til venstre betragter vi en beholder med vand, der er i hvile. Vi tænker os nu, at vi har afgrænset to vandmængder. Til venstre en kegleformet vandmængde og en tynd cylindrisk vandmængde, der forneden forbindes til én vandmængde med et tyndt, vandret rør. Og til højre en vandmængde, der har form som et stykke bugtet rør. Da vi ikke tror på telekinese, er der stadig ligevægt i alt vandet i beholderen. |
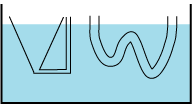 |
Vi erstatter nu de tænkte punkterede grænseflader for de to vandmængder med mikometertynde, stive skillevægge. Det ødelægger ikke ligevægten. Det siger vores fysiske intuition os. De stive skillevægge forlænges et lille stykke op over vandoverfladen. |
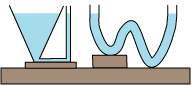 |
Nu er vores to vandmængder skilt fra resten af vandet i beholderen med stive vægge. Så kan vi uden at ændre ligevægten inde i vandmængderne fjerne beholderen og resten af vandet i den. Og så ser vi, at vi har argumenteret for, at når man hælder vand i to forbundne kar og lader vandet falde til ro, da står det lige højt i begge kar. Forhåbentlig synes læseren, at argumentet er overbevisende. Ikke desto mindre er resultatet overraskende: Skulle man ikke tro, at den store vandmængde i den kegleformede beholder ville presse vandet i den tynde cylinder højt op? |
Stevins resultat er altså:
| Når man hælder væske i to kar, der nede i væsken er forbundet med et rør fyldt af væske, vil væsken, når den er faldet til ro, stå lige højt i begge kar. |
Stevin undersøgte også trykket i en væske. Hans målinger viser, at han definerede trykket i et
punkt
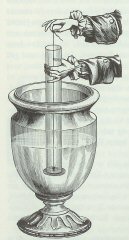 |
Billedet til venstre viser, hvordan Stevin målte et opadrettet tryk. Med snoren holder han den lille lette plade forneden tæt trykket op mod glasrøret, indtil glasrørets nederste ende er kommet derned, hvor han vil måle trykket. Så slipper han snoren og lægger forsigtigt blyhagl ned i røret, indtil pladen skubbes nedad, væk fra røret. Vægten af haglene plus pladen er så det opadrettede tryk på pladen. Resultatet af forsøgene var, at når man afgrænser en lille vandret flade nede i en væske, da vil det opadrettede tryk på fladen være lig vægten af den væskesøjle, der ligger lodret over fladen. Det nedadrettede tryk på fladen har naturligvis samme størrelse, ellers ville der jo opstå bevægelse i væsken. |
 | Det store apparat i midten benyttede Stevin til måling af det
nedadrettede tryk på en flade. Den flade, der skal måles på, er et stempel, der sidder nede ved
IK under
cylinderen i midten. Stemplet og dets korte cylinder er vist foroven til højre. Der trækkes opad i
stemplet af de to snore op til vægtstængerne for oven. Der hældes så
væske i cylinderen op til den ønskede væskehøjde, og dernæst udskiftes lodderne L og M, indtil
vægtstængerne holder ligevægt med stemplet. Bagefter kan man så udskifte cylinderen i midten med
et af de andre kar P og R. (I litteraturen kalder man karrene for "Pascals vaser".)
Resultatet er, at Stevin ved forsøg
efterviste, at trykket nedad nede i en væske alene afhænger af den lodrette afstand til overfladen
(og af væskens massefylde),
og at trykket er lig vægten af en (tænkt) væskesøjle , der befinder sig lodret over stemplet. Vi skriver
"tænkt", fordi
det også gælder, når cylinderen (som P) har mindre diameter end stemplet.
Apparatet kan også bruges til at måle trykket i vandret retning. Det sker ved, at man udskifter cylinderen i midten samt stemplet nedenunder med apparatet ST til venstre. Dette apparat har forneden et terningformet kar, som til højre har et stempel, der kan bevæge sig i vandret retning. De tre andre sider har glasvægge, og foroven er der et hul, der passer til glassene. To snore fra stemplet går til venstre rundt om en lille trisse og op til vægtstængerne. Når man hælder væske i, bliver rummet med trissen altså også fyldt med væske, der trykker til højre på stemplet. Med dette apparat kunne Stevin eksperimentelt vise, at trykket i vandret retning er det samme som det lodrette tryk i samme dybde. Derfor kan man tale om trykket et bestemt sted nede i en væske, uden at nævne hvilken retning man tænker på. |
Med ovenstående forsøg og tankeeksperimenter har Stevin etableret et bæredygtigt fundament for
hydrostatikken. "Bæredygtigt" kalder vi det, fordi man ud fra Stevins resultater kan besvare en masse
spørgsmål om væsker i ligevægt.

| Opgave 24 Hvor virker den kraft, der holder juicen et stykke oppe i sugerøret? |
4. Stevins sluseport
Vi afslutter denne gennemgang af Stevins resultater med et eksempel, der skyldes Stevin selv. Som nævnt i biografien beskæftigede Stevin sig også med sluser, og i eksemplet finder man faktisk ud af, hvor man lettest kan trykke på en sluseport, når man skal holde den lukket.
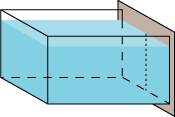 |
Vi kigger på et kar med vand, men vi har udskiftet den højre side af karret med en plade, som skal trykkes ind mod karret for at forhindre vandet i at løbe ud. Hvor skal vi trykke, hvis vi ønsker at trykke så lidt som muligt? Hvis man trykker ude mod den ene side, skal man trykke meget hårdt for at forhindre, at vandet i den anden side trykker pladen væk fra karret. Så man skal trykke midtpå, på ydersiden, der, hvor den punkterede linie er tegnet. Og så igen, hvis man trykker langt nede (eller oppe), så skal man trykke meget hårdt for at forhindre, at vandet foroven (eller forneden) trykker pladen væk fra karret. Så et eller andet sted i nærheden af midten skal man trykke. Men ikke lige i midten, for vandet forneden trykker jo mere udad (mod højre) end vandet foroven. |
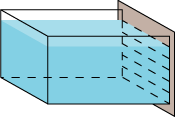 |
For at løse problemet deler vi nu højre side op i smalle strimler. De skal have samme bredde alle sammen. Så er trykket på et sted i en af strimlerne nogenlunde det samme hele vejen tværs over. |
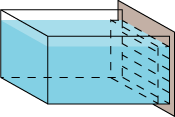 |
Det samlede tryk på den nederste strimmel er lig vægten af den vandplade, der er tegnet på figuren. Dens tykkelse er lig med afstanden mellem strimlerne. |
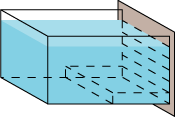 |
Den vandplade lægger vi nu ned, så den støder op mod den brune forplade. Så er trykket på den nederste strimmel lig med vægten af pladen. |
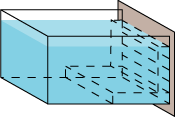 |
Så kigger vi på den næstnederste strimmel. Trykket på den er lig vægten af den vandplade, der er tegnet på figuren. Dens tykkelse er lig med afstanden mellem strimlerne. |
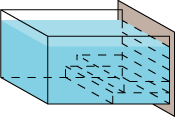 | Nu lægger vi den plade ned. Så er trykket på den næstnederste strimmel lig med vægten af pladen. |
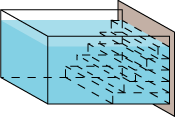 |
Sådan fortsætter vi, indtil vi får en trappe, der når helt op til overfladen. Hvis alle pladerne trykker mod højre med deres egen vægt, vil trappen altså i ethvert brunt punkt trykke lige så meget mod højre, som vandet i karret gør. |
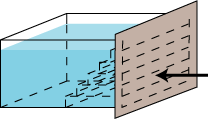 |
I det følgende tænker vi os nu, at alle pladerne trykker mod højre med deres egen vægt i stedet for at trykke nedad. Så kan opgaven formuleres således: Hvor højt oppe skal den sorte trykpil placeres, hvis den skal kunne balancere med trappen på pilespidsen? Hvis man sørger for det, opnår man nemlig, at man ikke spilder overflødige kræfter på at trykke på karrets kanter. |
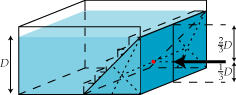 |
For at svare på det spørgsmål laver vi de oprindelige strimler papirtynde. Så bliver trappen erstattet af det mørkeblå prisme, der er vist på denne figur. Som før tænker vi os, at vægten virker mod højre. Spørgsmålet er nu: Hvornår kan pilen have prismet balancerende på spidsen. Det kan den - som allerede Archimedes vidste - når pilen peger på prismets tyngdepunkt. Tyngdepunktet er tegnet rødt på figuren. Før vi kan finde tyngdepunktet, må vi lige fortælle, at en median går fra en vinkelspids i en trekant til midtpunktet af den modstående side. Man finder frem til tyngdepunktet således: Vi skærer prismet op i tynde trekanter med snitplaner parallelle med karrets forside. Hver af disse trekanter har tyngdepunkt i medianernes skæringspunkt. Derfor vil alle disse tyngdepunkter ligge på den vandrette punkterede linie. Det må prismets tyngdepunkt derfor også gøre (se Archimedes), og det må af symmetrigrunde ligge midt på den punkterede linie. Og til sidst bruger vi så en sætning fra matematikken, der siger, at medianernes skæringspunkt ligger 1/3 af vanddybden D over bunden, sådan som det er vist på figuren. |
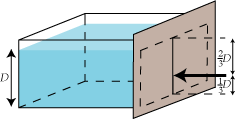 | Her er så slutresultatet: Hvis man på trods af vandtrykket vil holde den brune plade på plads med et så lille tryk som muligt, så skal man trykke midt for karret og 1/3 af vanddybden over bunden. |
Ovenstående er et fint lille eksempel på anvendt matematik: Ud fra de af Stevin eksperimentelt fundne fysiske love om tryk i vand kan man ad matematisk vej løse sluseportproblemet.
Man kan nu let finde ud af, hvor meget man skal trykke, det bliver jo vægten af prismet. Det er altså uafhængigt af karrets længde! Den metode, som Stevin bruger, er en forløber for det matematiske begreb integration.
5. Konklusion
Stevin er et tidligt eksempel på den nye tids fysikere: En borgerlig mand, der lever i et samfund,
hvor han frit kan udtrykke sig - i hvert fald om fysik. En mand, der ud over sit fag interesserer sig
for andet i samfundet, og som - på samfundets præmisser - bidrager til det, også uden for sit fagområde.
Ole Rømer er et dansk eksempel på en fysiker af den slags. Læs mere om Stevin i biografien.
| Hvis du støder på et ord, hvis betydning du ikke kender, så søg på ordet. |