Forside Søgning Liste

I sit arbejde med skråplanet fandt Stevin ud af, at betingelsen for ligevægt på figuren til højre er, at masserne forholder sig som skråplanslængderne, altså at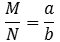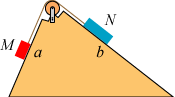

Stevin benyttede dette resultat ved videre undersøgelser, det førte ham tæt på kræfternes parallellogram - selv om begrebet kraft ikke var kendt på Stevins tid. Stevin betragtede opstillingen på figuren nedenfor til venstre, hvor højre skråplansside er lodret.

På figuren til venstre viser vi en rød klods med vægt M og tyngdepunkt T. Den står gnidningsfrit på den skrå side af skråplanet. Den kan holdes på plads på to måder, der begge er vist på figuren til venstre.

1. Man kan ophænge klodsen i sit tyngdepunkt i den ene ende af en ligearmet vægtstang, og hænge en grøn kugle med masse M i den anden ende af vægtstangen.
2. Alternativt kan man fastholde M med en snor, som er parallel med skråplanet og går op over en trisse og ophænge en vægt N i den anden ende af snoren. Så er der ligevægt, hvis N opfylder ligningen ovenfor.

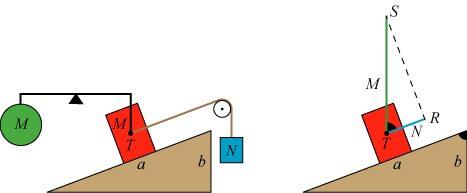
Situationen beskrives på figuren ovenfor til højre, hvor det grønne liniestykke har længde M ( det er lige meget hvilke enheder, man bruger ), og symboliserer den opadrettede vægt. Tilsvarende symboliserer det blå liniestykke, der er parallelt med skråplanet, og som har længde N, den "skrå vægt", som stammer fra det blå legeme. Fidusen er nu, at trekant RST dels har den sorte vinkel fælles med skråplanet og dels har sideforholdet M/N lig med det tilsvarende sideforhold a/b i skråplanets trekant. Heraf følger, at RST er ensvinklet med skråplanet. Vinkel R i trekant RST er derfor en ret vinkel. Stevin har dermed bevist følgende:

I dag ville vi sige, at tyngdens komposant i en skrå retning fås ved retvinklet projektion af tyngden på den skrå retning. Det er tæt på kræfternes parallellogram, men man får først en tilfredsstillende formulering, når man gør sig klart, at der skal to skrå retninger til, før begrebet en krafts komposant er veldefineret. Det var Stevin åbenbart klar over, for han fortsatte argumentationen på en måde, som er meget fængslende:

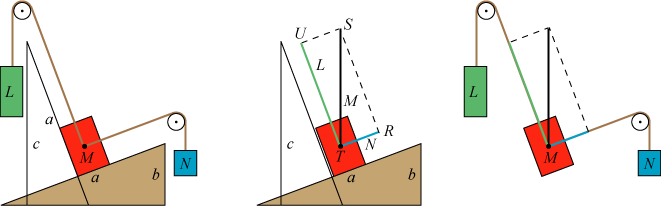
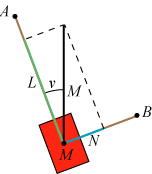
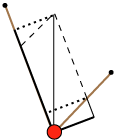
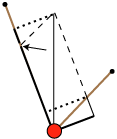
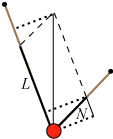
Mens man beholder M og det blå lod, anbringer man et skråplan magen til det brune, sådan som det er vist på to af figurerne ovenfor. Dernæst fjerner man M´s tryk på det brune skråplan ved hjælp af det grønne lod. Dets vægt L bestemmes af ligningen

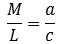
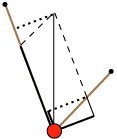
Ved at bruge den indrammede sætning på det nye skråplan får man, at det grønne lods træk fås ved retvinklet projektion af det sorte liniestykke på den stejle skrå retning, som det er vist på figuren i midten. Men nu trykker M ikke på nogen af skråplanerne, og vi kan derfor fjerne dem, uden at der sker noget, som det er vist ovenfor til højre.

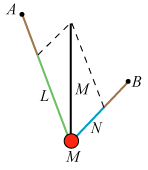
Nu er der jo ligevægt. Derfor kan man fastgøre de to snore i punkterne A og B lige under trisserne, og fjerne lodder og trisser. Så får vi figuren, der er vist til venstre. Resultatet er følgende: I stedet for at løfte med styrken M lodret opad kan man foretage to skrå løft, der står vinkelret på hinanden. Størrelserne L og N af de skrå løft fås ved retvinklet projektion af M på de skrå retninger. Når man ophænger en partikel med vægt M i to snore, der står vinkelret på hinanden, bliver trækket i snorene L = Mcosv og N = Msinv. Hvis f.eks. M = 10 kg og v = 20°, bliver L = 10·cos10° = 9,4 kg, og N = 10·sin10° = 1,7 kg. Snorene bærer altså mere end de 10 kg. Det er en stærkt begrænsende forudsætning for ovenstående resultater, at de to snore skal stå vinkelret på hinanden. Det var Stevin godt klar over, og han nævner da også, men uden bevis, at forudsætningen er unødvendig.

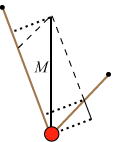
Hvis man fjerner forudsætningen om, at de to snore skal være vinkelret på hinanden, bliver resultatet lidt anderledes: Det lodrette løft af M kan erstattes af to skrå løft, hvis størrelser L og N findes ved hjælp af det parallellogram, der er vist på figuren til højre. Parallellogrammet er en tidlig forløber for det begreb, der senere blev kaldt kræfternes parallellogram. 100 år senere formulerede Newton den generelle regel om kræfternes parallellogram. Han var sandsynligvis inspireret af Stevin.

Stevin begrundede som nævnt ikke parallellogramreglen. Nedenfor giver vi et bevis, som vi har fra la Cour.

Partiklen holdes på plads af et lodret løft af størrelsen M	Det lodrette løft kan erstattes af to sorte skrå løft, der er vinkelrette på hinanden	Det lange sorte løft deles i to ved pilen, et stort for neden og et lille foroven.	Det lille sorte løft forskydes ned til sin naturlige plads. Så er de to korte løft vinkelrette på hinanden	Ifølge den beviste sætning kan de to løft så erstattes af det viste sorte løft N.

Hvis du støder på et ord, hvis betydning du ikke kender, så søg på ordet.