| Forside Søgning Brugsanvisning |
| Ind til listen: |
Mere om Thales fra Milet
1. Indledning
Thales fra Milet levede ca. fra år -624 til år -546; han blev altså ca. 78 år gammel. Hans holdning var ikke baseret på overtro, men på rationelle argumenter. F.eks. var der dengang mange der troede, at jordskælv var gudernes afstraffelse af mennesker. Thales foreslog en mere rationel forklaring: Hvis Jorden var en ø i et kollosalt hav af vand, så kunne et jordskælv fremkomme hvis Jorden stødte sammen med en anden ø i havet. Denne forklaring minder om nutidens, hvor man siger at kontinentpladerne bevæger sig i forhold til hinanden, og skaber jordskælv ved sammenstød. Der er intet skriftligt bevaret fra Thales hånd. Senere filosoffer har dog berettet om videnskabelige resultater fundet af Thales fra Milet.
2. Forudsigelse af en solformørkelse
Den 28. maj år -585 fandt der en solformørkelse sted. Den havde Thales forudsagt, og det var bemærkelsesværdigt, for på denne tid var astronomien, såvidt vi ved, ikke nævneværdigt udviklet. Nedenfor beskriver vi den viden, som Thales må have været i besiddelse af, for at kunne forudsige en solformørkelse.
Solformørkelse Måneformørkelse
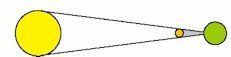
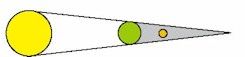
| På billedet kan man se, at når Månens skygge rammer Jorden dannes der et lille bitte område, hvor Solen ikke kan ses, hvor der altså er en solformørkelse. På grund af Jordens rotation flytter skyggeområdet sig hurtigt, så der dannes en smal stribe på Jorden, hvorfra formørkelsen kan iagttages. Formørkelsen kan også ses uden for den smalle stribe, men så er det ikke hele Solen, der er formørket. | På billedet kan man se, at det er anderledes når der er tale om en måneformørkelse. Så er Jordens skygge så bred, at Månen i længere tid befinder sig i skyggen. Sandsynligheden for at opleve en måneformørkelse er altså langt større end sandsynligheden for at opleve en solformørkelse. |
| På billedet til højre viser vi nogle afgørende ting, som Thales må have vidst, før han kunne forudsige en solformørkelse. Den store firkant er den plan, som Jorden bevæger sig i, i dens bane om Solen. Månens bevægelse omkring Jorden foregår i en anden plan. Den danner en vinkel på 5° med Jordens baneplan, og den bevæger sig sammen med Jorden, sådan som man kan se på billedet. | 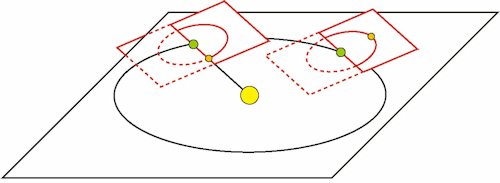 |
I den situation, der er vist til venstre befinder Månen sig mellem Jorden og Solen. Der er altså en solformørkelse. Et halvt år senere befinder Jorden sig mellem Solen og Månen, og der er derfor em måneformørkelse. Der kan ikke være en formørkelse, hvis Månen ikke ligger i Jordens baneplan.
Jeg gætter på, at Thales viden om de beskrevne forhold kan være tilstrækkelig til, at han kunne forudsige en solformørkelse. Men det kræver, at han i en lang årerække har holdt øje med Månens og Solens bevægelser.
3. Thales geometriske resultater
Vi beskriver her fire geometriske sætninger, der beskrives af Thales. Thales var tidligt på den. Matematikeren Euklid, der grundlagde geometrien, arbejdede omkring år -300.
| Thales nævner, at hvis A og C er endepunkter af en halv cirkel, og hvis B er et punkt på cirklen, så er vinkel ABC ret. Vi kender ikke Thales bevis, men på figuren til højre illustrerer vi et bevis. Man skal vide, at når en trekant har to ens sider, så har den også to ens vinkler. Derfor er der som vist to vinkler af størrelse x, og to vinkler af størrelse y. Da vinkelsummen i en trekant er 180 grader er 2x + 2y = 180 grader. Derfor er x + y = 90 grader, hvilket skulle bevises. | 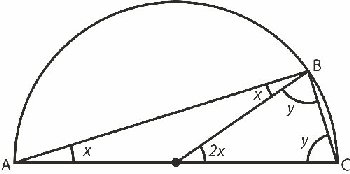 |
Thales anden geometriske figur:
| Thales nævner også, at hvis man tegner to linjer der skærer hinanden i et punkt A, og hvis man derefter tegner to parallelle linjer der skærer linjerne gennem A i DE og BC så vil AD/AB=AE/AC=DE/BC. Man kender ikke datidens argument. I nutiden vil man bare sige, at trekant ABC fås af trekant ADE ved multiplikation ud fra A med forholdet AB/AD | 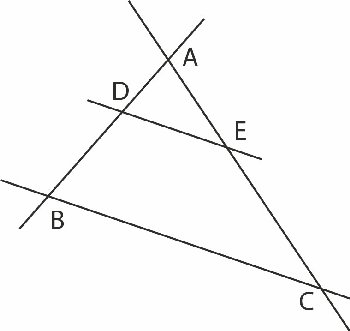 |
Thales tredie geometriske figur:
| Thales nævner også, at hvis ABC er en trekant, og hvis D er det punkt på BC der ligger sådan, at linjen AD halverer trekantsvinklen A, så er forholdet mellem AB og AC lig med forholdet mellem BD og CD.
Beviset for denne sætning er kompliceret, og man ved ikke hvordan Thales fandt frem til resultatet.
I tilknytning til figuren til højre gennemgår jeg nu det bevis for sætningen, som 200 år senere blev givet af den berømte matematiker Euklid. Det første Euklid gjorde var at tegne linjestykket CE som er parallelt med DA og som ender i punktet E, der ligger på forlængelsen af BA. Så er de tre røde vinkler lige store. Linjerne AC og AE danner derfor samme vinkel med parallellerne. Linjestykkerne AC og AE må derfor være lige lange, lige som de to linjestykker på figuren for oven. Det følger derfor af resultatet i Thales anden figur, at D deler BC i to stykker, hvis forhold er lig forholdet mellem siderne AB og AC. | 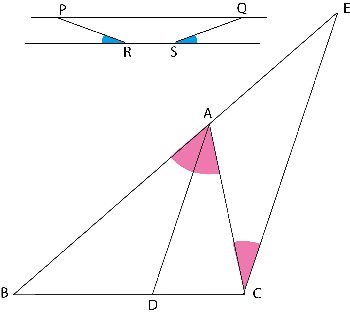 |
Thales fjerde geometriske figur:
| Det fortælles at Thales målte højden af en pyramide ved at måle længden af pyramidens skygge på et tidspunkt hvor hans egen skygge var lig hans højde; - længden af skyggen skulle måles fra det punkt der lå midt inde under pyramiden. Metoden er korrekt, som man let ser på figuren til højre. | 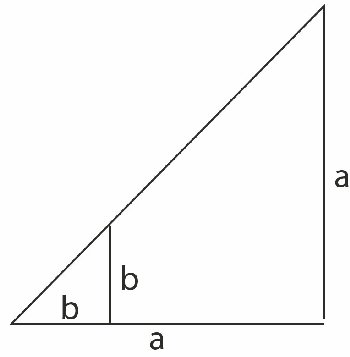 |
| Hvis du støder på et ord, hvis betydning du ikke kender, så søg på ordet. |