Forside Søgning Liste

Ordet trigonometri betyder trekantsberegning. De trigonometriske funktioner kan anvendes både til beregning i plane trekanter og i trekanter på en kugleflade, sfæriske trekanter. Siderne i en sfærisk trekant er storcirkelbuer. Trigonometri stammer fra oldtidens Byzants og fra Indien. Herfra blev den videre udviklet af araberne for så at komme til Vesteuropa med Regiomontanus. Trigonometri var meget vigtig for landmåling og astronomi, og bruges i dag overalt i fysikken.

Af hensyn til dem, der næsten har glemt de trigonometriske funktioner, følger her en kort omtale af dem. Vi måler her vinkler i radianer. For en vinkel v mellem 0 og π/2 er sin v, cos v og tan v defineret ved hjælp af de to retvinklede trekanter på figuren nedenfor, hvor der er valgt en tilfældig længdeenhed.

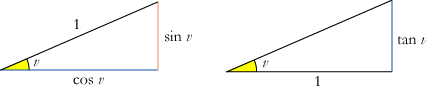
Hvis f.eks. v = π/4 (dvs 45°) fås, at sin v = cos 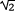v = ½ og tan v = 1.

For en vilkårlig værdi af v defineres funktionerne ved hjælp af figuren herunder:

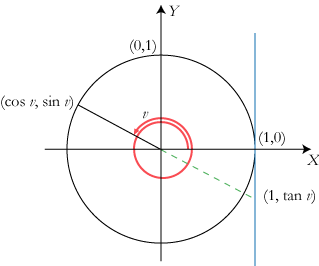
I et XY-koordinatsystem tager vi et liniestykke fra (0,0) til (1,0). Dette liniestykke drejer vi vinklen v om koordinatsystemets begyndelsespunkt sådan som det er vist på figuren, hvor v er ca 8,9 radianer. Hvis v<0 drejes den modsatte vej. (sin v, cos v) er da defineret som koordinaterne til det drejede liniestykkes endepunkt. 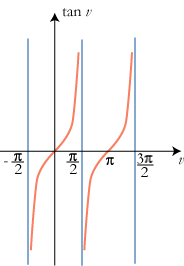tan v er defineret som Y-koordinaten til skæringspunktet mellem det drejede liniestykkes forlængelse og den blå linie. For v=½π+nπ er tan v ikke defineret, når n er et helt tal. Ved hjælp af to ensvinklede trekanter kan man se, at tan v = sin v / cos v. 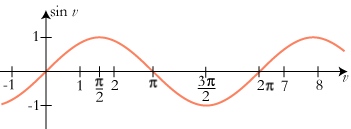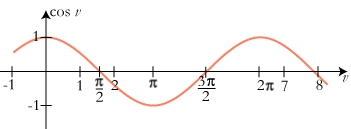Graferne for de tre funktioner er vist på figurerne nedenfor:

Der findes et omfattende system af formler, der forbinder de trigonometriske funktioner. Den vigtigste af disse formler er den såkaldte idiotformel

Formlen aflæses af den retvinklede trekant, som vi brugte ved definitionen af cos og sin. Der er en anden formel, som vi nævner her af hensyn til anvendelser i fysik:

når

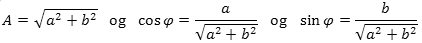
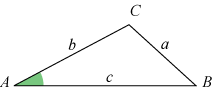Ordet trigonometri betyder trekantsmåling. Og faktisk blev trigonometrien oprindelig udviklet med henblik på trekantsberegninger. Hvis vi f. eks. i trekanten på figuren kender de tre sider a, b og c kan den grønne vinkel A beregnes af formlen

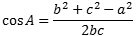
Hvis specielt b² + c² = a² bliver tælleren 0, og A må derfor være 90°. Formlen ovenfor kaldes cosinusrelationen. Man kan også vise, at

,

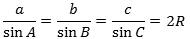hvor R er radius i trekantens omskrevne cirkel. Denne formel kaldes sinusrelationen.

Hvis du støder på et ord, hvis betydning du ikke kender, så søg på ordet.