|
Forside
Søgning
Liste |  |
Om måleenheder for vinkler
En vinkel er et lidt mere abstrakt begreb end f.eks. længde, areal og vægt. Det er derfor overraskende, at enheden grad for vinkelmål er den ældste enhed, der stadig bruges. Det hænger sammen med, at alle vinkler ligger mellem 0 og en hel omgang, mens længde, areal og vægt er ubegrænsede opadtil. Inddelingen af en hel omdrejning i 360° er naturligvis kulturbestemt. Den er indført i Mesopotamien, måske ca. år -1500. At man valgte 360 grader kan hænge sammen med, at man brugte 60-talssystemet. Men det kan også hænge sammen med, at året har ca 360 dage. Faktisk delte den kinesiske astronom Shih Shen ca. -360 cirklen i 365¼ grader svarende til antallet af dage i et år.
Til brug ved nøjagtige undersøgelser delte man en grad i 60 lige store dele. Hver af dem
kaldes et bueminut, 1´, så 1° = 60´. Timen og graden deltes altså begge i 60 dele, som vi
kalder minutter. Vi ved ikke, om babylonerne brugte samme ord for de to forskellige begreber.
På samme måde delte man et bueminut i 60 buesekunder, så 1´ = 60". Figuren nedenfor giver et indtryk af
størrelsen af de tre enheder:
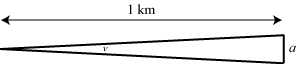
| v | 1° | 1´ | 1" |
| a | 17 meter | 29 cm | 5 mm |
Tabellen nedenfor viser målenøjagtigheden for vinkelmåling på himlen udført af
udvalgte betydelige astronomer.
| Astronom | Hipparchos | Tycho Brahe | Ole Rømer | James Bradley | Wilhelm Bessel |
| Årstal | -150 | 1580 | 1675 | 1728 | 1838 |
| Målenøjagtighed | 10´ | ½´ = 30" | 5" | 1" | 1/10 " |
De resultater, man finder i matematikken, er ikke kulturbestemte, - derimod er det
kulturbestemt,
om de findes.
Gradmålet er kulturbestemt, og bl.a. af denne grund vil matematikere anvende et andet,
matematisk set mere naturligt vinkelmål. Det kaldes en radian, og er ca. 57,2958°.
Hvordan i alverden
har man fundet på det? Jo, en vinkels radiantal er defineret på følgende måde: Tegn en cirkel med radius 1 og
med centrum i vinklens toppunkt. Vinklens mål i radianer er da længden af den cirkelbue, som
vinklen afskærer. Læg mærke til, at radianmålet for en vinkel ikke afhænger af, hvilken
længdeenhed, man bruger
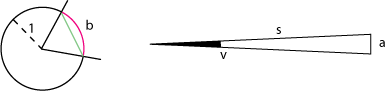
Radianmålet for vinklen på figuren til venstre er altså længden b af den røde cirkelbue. Faktisk er b ca 1,24 radianer.
Det er let at finde sammenhængen mellem vinkelmålet v for en vinkel og radianmålet r for den samme vinkel. Da 360° er 2π radianer, er sammenhængen den, at
Figuren ovenfor til højre illustrerer en hovedpointe ved radianmålet:
Når vinklen v, som måles i radianer, er lille, gælder med meget god
tilnærmelse, at a=v·s.
Grunden er, at korden og buen er meget nær ved at være sammenfaldende. Heraf følger videre,
at arealet af trekanten med meget god tilnærmelse er ½·s2·v.
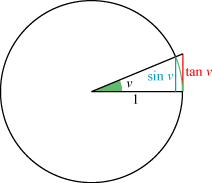
På figuren betegner v radiantallet for den grønne vinkel, dvs længden af den grønne cirkelbue. Der er ikke meget forskel på v, sin v og tan v. Og de små forskelle, der er, bliver mindre og mindre, hvis man vælger mindre værdier for v. Hvis vinklen f.eks. er 1° er
| v | = | 0,01745329 |
| sin v | = | 0,01745241 |
| tan v | = | 0,01745506 |
Så i praksis kan man godt regne med, at når vinklen v måles i radianer og er lille,
da vil v = sin v = tan v.
| Hvis du støder på et ord, hvis betydning du ikke kender, så søg på ordet. |