|
Forside
Søgning
Liste |  |
Om bølgebevægelser
Allerede i oldtid og middelalder var der nogen viden om lydbølger, især i forbindelse med musik, men et egentligt studium af bølgebevægelser startede først med Huygens´ undersøgelser i slutningen af 1600-tallet.
Det særlige ved en bølgebevægelse er, at det er en form, der bevæger sig fremad. Det, som formen består af, bevæger sig kun ganske lidt. Lad os starte med to eksempler fra dagligdagen:
Når tilskuerne til en fodboldkamp laver bølge, så bevæger bølgen sig hele vejen hen ad langsiden, mens den enkelte tilskuer slet ikke bevæger sig den vej, men blot rejser sig og sætter sig på det rigtige tidspunkt. Sådan en bølge kaldes en transversalbølge, fordi tilskuernes bevægelser går på tværs af bølgens bevægelsesretning.
Når vinden en dag i eftersommeren blæser hen over en kornmark, sker det, at der i kornet dannes en bølge, der bevæger sig i vindens retning. "Der løb en iling gennem kornet," sagde Jeppe Aakjær. Kornaksene bevæger sig på langs af vindretningen, og bølgen kaldes derfor longitudinal.
Vi starter her med en almen introduktion til begrebet bølgebevægelse.
Vandbølger
Først betragter vi bølger på en vandoverflade.Vi vil beskrive, hvordan vandpartiklerne i overfladen bevæger
sig, når vandbølgerne ruller fremad. Det er svært at se ude i naturen, og dér er det også meget forvirret.
I stedet tænker vi os et ideelt forsøg, hvor bølgerne løber i et langt, dybt, smalt
kar med glasvægge. Vi tænker os, at bølgerne vedligeholdes i den venstre ende af karret, ved at en genstand bevæges op og ned
i en bestemt takt. Karret skal være så langt, at
bølgerne ikke reflekteres fra den anden ende. Hvis man så kommer lidt savsmuld eller lignende ned i vandet
og rører rundt, inden man starter forsøget, så kan man se, hvordan de små vand"partikler" bevæger sig. Og det
viser sig, at de i hvert fald tæt ved overfladen bevæger sig i cirkler. Længere nede bevæger vandpartiklerne
sig mindre, og man skal kun et par bølgelængder ned, før bølgebevægelsen ikke kan spores. På animationen
nedenfor viser vi
nogle vandbølger, der bevæger sig mod højre. Der er også vist 20 sorte overfladepartikler og deres
cirkulære
banekurver. Alle overfladepartikler bevæger sig i cirkulære baner med samme radius.
 | |
 |  |
På animationen er bølgerne ret spidse opadtil. Det er almindeligt i naturen, og i havet får den slags
bølger tit en strimmel skum hen langs spidsen. De vandpartikler, der er oppe i en spids, bevæger sig
i samme retning som bølgerne. Men læg mærke til, at nede i bølgedalene bevæger overfladepartiklerne sig
i modsat retning af bølgerne. Det er en uventet ting, som man let kan iagttage i naturen ved at smide en
pind eller en prop i vandet, f.eks. fra en badebro.
| Opgave 13 Kig på en sort partikel i det øjeblik, hvor den er højest oppe. Bevæger den sig i dette øjeblik hurtigere fremad end bølgerne? |
Der er fem vigtige størrelser, som man skal kende, når man beskæftiger sig med bølgebevægelser. Det er bølgelængden λ, hastigheden v, svingningstiden s, frekvensen f og fasen for hver enkelt partikel. De fem størrelser defineres således:
- Bølgelængden λ er afstanden mellem to på hinanden følgende bølgetoppe. På animationen ovenfor er λ = 0,8 meter.
- Hastigheden v er den hastighed, som bølgerne bevæger sig med. På animationen ovenfor tager det en bølgetop 44 sekunder at flytte sig målestokkens 2 meter fremad. Hastigheden er derfor 2/44 m/sek = 0,045 m/sek.
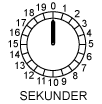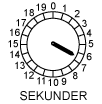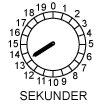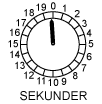
- Den tid, en af de sorte partikler er om at bevæge sig én gang rundt i sin bane, kaldes svingningstiden s. Lad os sige, at til tidspunktet T er en bestemt af de sorte partikler oppe på en bølgetop. Der går så s sekunder, før partiklen igen er oppe på en bølgetop. s er altså også den tid, bølgerne er om at bevæge sig en bølgelængde fremad. På animationen ovenfor kan man let kontrollere, at svingningstiden er 18 sek.
- Frekvensen f er antallet af svingninger - i dette tilfælde antallet af cirkelomløb -, som den enkelte partikel udfører pr tidsenhed. Når svingningstiden er s, må partiklen udføre 1/s svingning hvert sekund. Frekvensen og svingningstiden er altså reciprokke, f·s = 1. Når man stiller sig i et fast punkt, passerer der som nævnt en bølge, hver gang der er gået s sekunder. Derfor passerer der 1/s = f bølgetoppe i sekundet. Frekvensen kan også findes ved, at man stiller sig i et fast punkt, og tæller antallet af bølgetoppe, der passerer pr. tidsenhed. På animationen ovenfor tager det 18 sekunder for en af de sorte vandpartikler at løbe én gang rundt i sin cirkel. Frekvensen er derfor f = 1/18 sek-1 = 0,056 sek-1. Enheden for frekvens er tid-1. Enheden sek-1 er så vigtig, at den har fået et specialnavn. Den kaldes en hertz, forkortet 1 Hz. Vandbølgernes frekvens er altså 0,056 Hz.
- Fasen for en partikel er et mål for, hvor langt partiklen er i sin periodiske bane. To partikler siges at være i samme fase, når de f.eks. er i højre yderstilling samtidig. F.eks. er alle de partikler, der på et bestemt tidspunkt er oppe på en bestemt bølgetop i samme fase; de ligger på en linie vinkelret på skærmen. To partikler, hvoraf den ene er på en bølgetop, og den anden samtidig er i bunden af en bølgedal, er i modfase. På animationen ovenfor er partiklerne på 2. og 7. cirkel fra venstre i fase.
Hvis man stiller sig i et fast punkt og kigger på bølgerne, så ser man, at der passerer f bølger
hvert sekund. Men da afstanden mellem to nabobølger er λ, har bølgerne på et sekund bevæget sig
stykket f·λ fremad. Der gælder derfor formlen
v = f·λ
Denne formel gælder for alle typer af bølgebevægelser.
Studiet af vandbølger er kompliceret. Vandbølger er hverken transversale eller longitudinale. Hvis bølgelængden er stor, og vanddybden er større, er hastigheden proportional med kvadratroden af bølgelængden. Den er bestemt af formlen
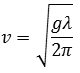
hvor g er tyngdeaccelerationen. For helt små bølgelængder, få cm, kommer overfladespændingen til at spille en større rolle end tyngdekraften. Så er det hele meget kompliceret.
Det er i øvrigt usædvanligt for bølgebevægelser, at hastigheden er afhængig af bølgelængden. Både for lydbølger og for lysbølger gælder det, at hastigheden er den samme for alle bølgelængder. Af formlen v = f·λ følger derfor, at det både for lyd- og lysbølger gælder, at hvis man fordobler bølgelængden, da bliver frekvensen halveret.
Lydbølger
Studiet af lydbølger startede allerede i græsk oldtid. Lydbølger studeredes især i sammenhæng med
musikkens toneskalaer. Her går vi over til at give en beskrivelse af, hvordan lydbølger forplanter sig.
Vi tænker os, at der er en lydgiver langt ude til højre. Det kan være en svingende streng eller en
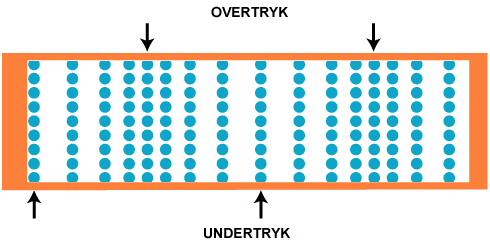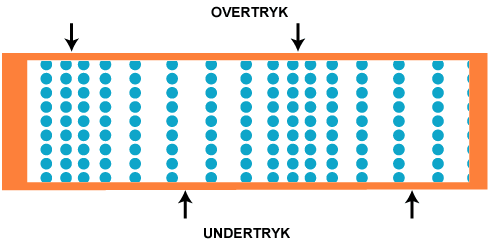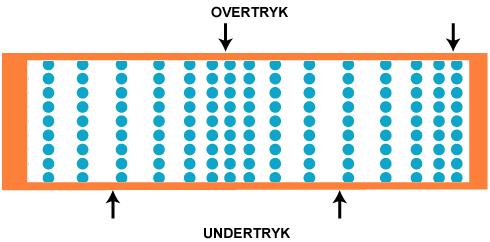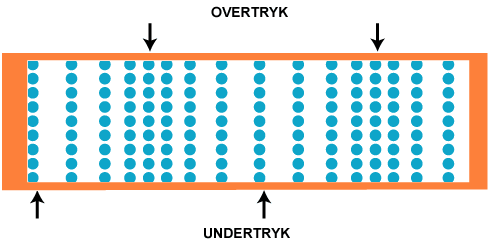
højttalermembran. Vi forudsætter, at den udsendte lyd er en ren tone med konstant styrke. På figuren
nedenfor viser vi et regelmæssigt net af 144 luftpartikler, og vi vil beskrive, hvordan disse luftpartikler
bevæger sig, efter at lyden er nået frem til dem.

Løst sagt forplanter lyden sig på den måde, at den svingende lydgiver sætter naboluftpartiklerne i
svingning med samme frekvens, dvs. antal svingninger pr. sek. Disse trykker så igen på deres naboer, og sådan fortsætter det, så lyden
forplanter sig. På animationen nedenfor viser vi, hvordan vores 144 partikler bevæger sig. Læg mærke til,
at hver enkelt partikel bevæger sig sådan , altså på animationen ikke mere end
ca. 1 cm frem og tilbage. Jo større udsving der er, jo større er lydstyrken. Svarende til vandbølgernes
bølgetop og bølgedal har vi her områder i rummet, hvor
der er overtryk og undertryk, og det er disse områder, der bevæger sig mod venstre, sådan som det er
vist med sorte pile på animationen nedenfor. Vi bruger udtrykket bølgetop, også når der er tale om overtryk eller
undertryk eller noget helt tredie.
Partikler på samme lodrette linie er i fase. I virkeligheden er der et lodret
plant
område vinkelret på skærmens plan med partikler i denne fase. En sådan plan kaldes en bølgefront. Vores animationer
foregår i skærmens plan, de er todimensionale. Men de forestiller normalt en bølgebevægelse i tre dimensioner, hvor
en bølgefront er todimensional. En plan bølgefront viser sig på vores figurer og animationer i reglen som et
liniestykke eller en kurve.
I teksten omtaler vi sådan en bølgefront (eller den bølge, som den er en del af) som plan eller f.eks. kugleformet.
Tæt på en lydgiver vil lydbølgerne i reglen være kugleformede eller i hvert fald krumme, men langt væk fra
lydgiveren bliver de i praksis plane.
På animationen er en partikel og dens to vandrette naboer
i tre forskellige faser.
Partiklerne i 1. og 9. lodrette søjle er i fase.
, altså på animationen ikke mere end
ca. 1 cm frem og tilbage. Jo større udsving der er, jo større er lydstyrken. Svarende til vandbølgernes
bølgetop og bølgedal har vi her områder i rummet, hvor
der er overtryk og undertryk, og det er disse områder, der bevæger sig mod venstre, sådan som det er
vist med sorte pile på animationen nedenfor. Vi bruger udtrykket bølgetop, også når der er tale om overtryk eller
undertryk eller noget helt tredie.
Partikler på samme lodrette linie er i fase. I virkeligheden er der et lodret
plant
område vinkelret på skærmens plan med partikler i denne fase. En sådan plan kaldes en bølgefront. Vores animationer
foregår i skærmens plan, de er todimensionale. Men de forestiller normalt en bølgebevægelse i tre dimensioner, hvor
en bølgefront er todimensional. En plan bølgefront viser sig på vores figurer og animationer i reglen som et
liniestykke eller en kurve.
I teksten omtaler vi sådan en bølgefront (eller den bølge, som den er en del af) som plan eller f.eks. kugleformet.
Tæt på en lydgiver vil lydbølgerne i reglen være kugleformede eller i hvert fald krumme, men langt væk fra
lydgiveren bliver de i praksis plane.
På animationen er en partikel og dens to vandrette naboer
i tre forskellige faser.
Partiklerne i 1. og 9. lodrette søjle er i fase.
 | |
 | 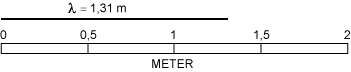 |
Animationen viser, hvordan partiklerne bevæger sig, når lydgiveren udsender en ren tone. Den tone, vi har valgt, er det midterste C på et klaver. Tonen frembringes af en streng i klaveret, der svinger frem og tilbage 259 gange i sekundet. Tonen har altså frekvensen f = 259 Hz, svarende til en svingningstid på 1/259 sek= 3,86 millisekunder (msek). Det kan man nogenlunde aflæse på uret. Lydens hastighed ved normalt tryk og temperatur er uanset bølgelængden v = 340 m/sek = 0,34 m/msek, det er den hastighed, som de sorte pile bevæger sig med. Det kan man groft skønne på animationen. Og endelig er bølgelængden λ afstanden mellem to på hinanden følgende sorte pile. Bølgelængden kan beregnes ved hjælp af formlen v = f·λ. Man får, at λ = v/f = 340/259 = 1,31 m. Den er afsat på animationens målestok. I en lydbølge bevæger hver enkelt partikel sig på en linie, der går i lydens retning. Lydbølger er altså longitudinale.
Når lydgiveren frembringer en ren tone, udfører hver enkelt partikel en sinusformet svingning bestemt ved formlen
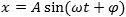
Her betyder x afstanden fra ligevægtsstillingen, regnet positiv til højre og negativ til venstre.
t er tiden, og A kaldes amplituden. På animationen er A = 0,5 cm. A
bestemmer lydstyrken. Den har nogenlunde samme værdi for partikler, der har nogenlunde samme afstand fra lydgiveren, men
værdien aftager med voksende afstand fra lydgiveren. Når man lægger 2π/ω til t, bliver tallet i
parentesen 2π større. x ændres derfor ikke. Det betyder, at svingningstiden T = 2π/ω,
så ω = 2π/T.
ω kaldes vinkelfrekvensen. Det er antallet af radianer vinklen under sinustegnet vokser med hvert sekund.
Den måles i enheden sek-1. Den er
bestemt af lydgiveren og har samme værdi for alle partikler, der deltager i bølgebevægelsen. Endelig kaldes φ for
partiklens fase. Partikler i samme bølgefront har pr. definition samme fase. Fasen er ikke fuldt bestemt af bevægelsen, den afhænger af
placeringen af tidens nulpunkt. På animationen ovenfor aftager fasen med π/4, for hver gang man rykker en søjle til venstre.
Det kan man se ved at iagttage, at partiklerne i en søjle er 1/8 svingningstid senere på den end dem i søjlen lige til højre. De skal
jo ligesom have et skub fra højre, før de bestemmer sig til at vende om.
Det stemmer med, at partiklerne i 1. og 9. lodrette søjle har samme fase. Og hvis f.eks. partiklerne i 1. søjle til højre svinger
efter ligningen
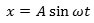
så vil partiklerne i 2. søjle fra højre svinge efter ligningen
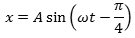
I 1. søjle er partiklerne i midterstilling for t = 0, men i 2. søjle er de der først, når t = T/8=π/4ω.
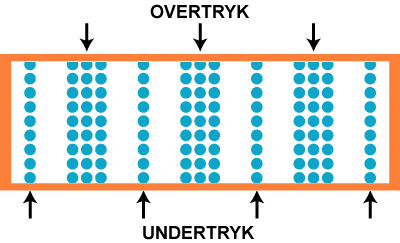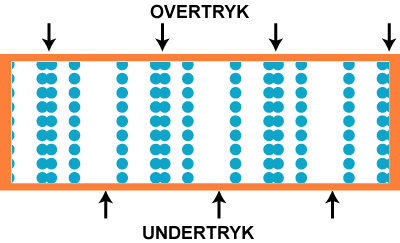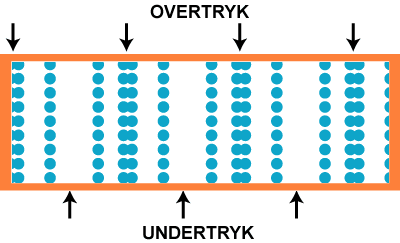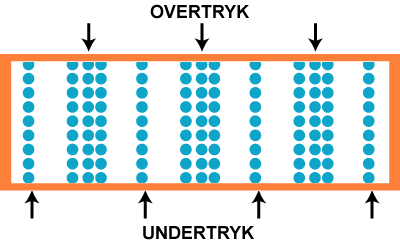
Vi slutter med at vise, hvordan det tager sig ud, hvis vi udskifter C-et med
frekvens 259 Hz med dets oktav oven over, det næste C til højre på klaveret. Det har dobbelt så stor
frekvens, så nu svinger luftpartiklerne sådan  , altså med frekvensen
518 Hz. Da hastigheden er den samme som før, bliver bølgelængden halvt så stor, som
den var før, altså 0,66 m. Det hele vises på animationen nedenfor:
, altså med frekvensen
518 Hz. Da hastigheden er den samme som før, bliver bølgelængden halvt så stor, som
den var før, altså 0,66 m. Det hele vises på animationen nedenfor:
 | |
 |  |
De sorte pile bevæger sig lige hurtigt på de to animationer. Lydens hastighed er jo uafhængig af bølgelængden. Vi ved ikke, hvem der først fandt ud af, at lydens hastighed er 340 m/sek = 1225 km/time. Det er ikke så svært. F.eks. husker jeg, at jeg som dreng så en smed stå på en mark og slå på noget jern med en hammer. Jeg stod noget væk, så lyden af hammeren nåede mig, når smeden havde hammeren hævet over hovedet. Den simple iagttagelse kan selvfølgelig bruges til beregning af lydhastigheden.
I løbet af 1600-tallet var der forsøg på at beskrive lys som en bølgebevægelse. Se under 1677 Huygens.
Forsøgene var vellykkede, men det var et problem, at man manglede "noget", som lysbølgerne kunne svinge i.
Lyset kan gå gennem både glas og det lufttomme rum, og hvad kan være begge disse steder, som lyset kan
svinge i? Sagen blev først endelig afklaret i løbet af 1900-tallet.
| Hvis du støder på et ord, hvis betydning du ikke kender, så søg på ordet. |