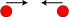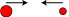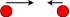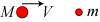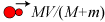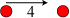Forside Søgning Liste

Descartes arbejder i mekanikken

1. Descartes om det frie fald

I sin omtale af det frie fald bruger Descartes "bevægelsens konfiguration", sådan som den er beskrevet af Oresme ca. 1350. Men Descartes har vist ikke rigtigt forstået Oresmes metode. Vi viser Descartes´ figur til højre. Descartes betragter et legeme, der falder frit fra A til B, og han vil undersøge, hvordan hastigheden vokser. AB deles i mange nummererede småstykker med vandrette linier. Disse linier beskrives noget uklart, f.eks.: "Linie 2 beskriver styrken af den påtrykte ("impressed") hastighed i det andet øjeblik." Meningen er sandsynligvis, at arealet mellem f.eks. linie 3 og linie 4 angiver den hastighedstilvækst, som legemet får, når det falder fra position 3 til position 4. Denne fortolkning passer med, at Descartes skriver, at "Sådan dannes trekant ABE, og den (s areal) repræsenterer tilvæksten i hastighed i den første halvdel af den afstand, som legemet falder." Denne fortolkning understøttes af den følgende bemærkning: "Da trapezet BCDE er tre gange større end trekant ABE, følger det, at legemet falder tre gange så hurtigt fra B til C som fra A til B. Dvs., at hvis det falder fra A til B i 3 øjeblikke ("moments"), så vil det falde fra B til C på 1 øjeblik."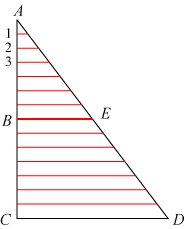

Den sidste slutning er ikke korrekt. Det er hastighedstilvæksterne, der forholder sig som 3 til 1, ikke faldtiderne. Og der er en fejl til:

Descartes antager, at hastighedstilvæksten er proportional med faldvejens tilvækst, dvs. at v = ks. (Den samme antagelse gjorde Galilei, inden han fandt faldlovene) Men i virkeligheden er hastighedstilvæksten pr. faldet cm omvendt proportional med kvadratroden af faldvejen. Der er intet af værdi i Descartes´ argumentation.

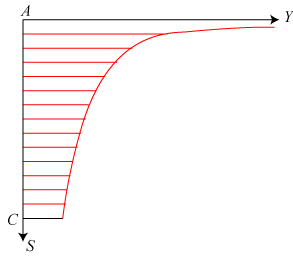Figuren til venstre viser, hvordan Descartes figur burde have set ud ifølge Galileis faldlove. I dag kan man godt tænke sig til, at hastighedstilvæksten pr. faldet mm må være (uendelig) stor til at begynde med. For da er hastigheden jo 0, og så er legemet meget lang tid om at falde 1 mm, og så har tyngdekraften lang tid til at accelerere legemet. Men den måde at tænke på var ikke så naturlig på Descartes´ tid, hvor begreberne ikke var afklarede. Vi bruger nu det SY-koordinatsystem, der er vist på figuren. Ligningen for kurven kan så findes således: Af Galileis faldformler følger, at . Heraf fås ved differentiation, at .

2. Descartes om stød mellem fuldstændig elastiske legemer.

Teorien om fuldstændig elastiske legemer blev afrundet af Huygens i 1652, så Descartes´ undersøgelser ligger tidligere end Huygens´. Begge fysikere bygger fremstillingen på aksiomer.

Selv om man ikke kan se det af aksiomerne nedenfor, ligger der til grund for dem, at bevægelsesmængde bevares. For Descartes var bevægelsesmængden af et legeme med masse M og hastighed v det positive produkt Mv. Den samlede bevægelsesmængde for flere legemer er summen af de enkelte legemers bevægelsesmængder. Descartes udtrykker i aksiomerne, at den således definerede bevægelsesmængde bevares under et stød mellem to elastiske legemer. Det er let ved forsøg at påvise, at bevægelsesmængden ikke altid bevares under stødet. Huygens påviste i 1652, ved hjælp af aksiomer, som også Descartes måtte anse for rigtige, at det er den med fortegn regnede bevægelsesmængde, der bevares. Det skal forstås på den måde, at en linie parallel med den retning, legemerne bevæger sig, orienteres med en pil i den ene ende. Så regnes en hastighed positiv, hvis legemet bevæger sig i pilens retning, og ellers negativ. Bevægelsesmængden Mv bliver så også regnet med fortegn. Huygens påviste i 1652 ud fra sine aksiomer, at det er denne med fortegn regnede bevægelsesmængde, der bevares under stødet.

I tabellen nedenfor gengiver vi de 6 første (af 7) af Descartes´ aksiomer, og til højre kommenterer vi dem.

Aksiom 1. Når to ens legemer støder sammen med samme hastighed, stødes de fra hinanden med samme hastighed som før stødet. Før stødet Efter stødet	Dette aksiom stemmer med erfaringen. Både Descartes´ og Huygens´ bevægelsesmængde bevares.
Aksiom 2. Når to forskellige legemer støder sammen med samme hastighed, vil kun det mindste legeme skifte bevægelsesretning, og de to legemer vil efter stødet følges ad med den hastighed, de havde før stødet. Før stødet Efter stødet	Forsøg viser, at aksiomet er forkert. Man kan også slutte det af det første aksiom. For hvis de to legemer er næsten lige store, vil de efter stødet bevæge sig næsten som beskrevet i aksiom 1. Descartes´ bevægelsesmængde bevares.
Aksiom 3. Hvis to ens legemer støder sammen med forskellige hastigheder, vil de følges efter stødet, i den retning det hurtige havde, og med en hastighed, der er gennemsnittet af de to begyndelseshastigheder. Før stødet Efter stødet	Forsøg viser, at aksiomet er forkert. Det kan man som før tænke sig til ved hjælp af aksiom 1. Descartes´ bevægelsesmængde bevares.
Aksiom 4. Hvis det ene af to legemer er fastgjort i hvile, og det andet støder ind i det, vil det andet skifte bevægelsesretning, men beholde hastigheden. Før stødet Efter stødet	Aksiomet er korrekt. Det falder uden for rammerne af Huygens´ stødteori, der handler om to legemer, der støder sammen, uden at der er andre kræfter som dem fra væggen her. Descartes´ bevægelsesmængde bevares.
Aksiom 5. Hvis et legeme med vægt m er i hvile og bliver stødt af et større legeme med vægt M og hastighed V, vil de to legemer følges ad efter stødet med det stores bevægelsesretning, og med en hastighed v = MV/(M+m) Før stødet Efter stødet	Forsøg viser, at aksiomet ikke er korrekt, legemerne følges ikke ad efter stødet. Både Descartes´ og Huygens´ bevægelsesmængde bevares.
Aksiom 6. Hvis et legeme C er i hvile og rammes af et lige så stort legeme B, vil B skubbe C fremad, og C vil skubbe (reflect) B. Hvis B til at begynde med har hastighed 4, giver det hastigheden 1 til C, og det bevæger sig selv tilbage med hastighed 3. Før stødet Efter stødet	Aksiomet er forkert. Sandheden er, som forsøg let viser, at B bliver liggende, og at C fortsætter med B´s fart. Descartes´ bevægelsesmængde bevares.

3. Descartes syn på fysik.

Man kan undre sig over, at Descartes fastholdt dette system af aksiomer, når der både var indbyrdes modstrid og manglende overensstemmelse med eksperimenter. Descartes var nok klar over, at der var problemer, men han kommenterede det på følgende måde:

"Det sker ofte, at man ved første blik finder uoverensstemmelse mellem iagttagelser og de regler, som jeg lige har beskrevet. Men grunden til det er klar. For aksiomerne forudsætter, at de to legemer er fuldstændigt hårde og så adskilte fra alle andre, at der ikke er noget andet nær dem, der kan hjælpe dem eller hindre deres bevægelse. Vi ser intet af denne slags i den virkelige verden."

Hos Jouguet finder man følgende velvalgte kommentar til dette:

"Dette citat er meget karakteristisk for Descartes´ tankegang. Han kunne iagttage naturen og drage slutninger af aksiomerne lige så godt som enhver anden. Men det var hans hensigt at genopbygge alting på en rational måde i overensstemmelse med principperne i hans filosofi. Han havde det synspunkt, at kilden til sikkerhed var i tankens magt alene. Det vides, at han ikke ønskede at antage de principper, som var accepteret i geometri og fysik, - og derudover kom han, ved at overdrive tiltroen til sit system, til at tilsidesætte tiltroen til eksperimenter."

Efter disse citater af betydelige mænd tillader jeg mig en yderligere kommentar: Jeg synes, at der er en lighed mellem Descartes´ holdning og holdningen hos platonikerne i oldtidens Grækenland. Begge steder forestiller man sig, at der bag vores uperfekte verden ligger en ideel, og at det må være filosoffernes væsentligste opgave ad tankens vej at finde frem til denne ideelle verden. Dette synspunkt bevirker ikke fremskridt i fysikken.

Hvis du støder på et ord, hvis betydning du ikke kender, så søg på ordet.
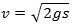
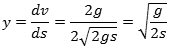