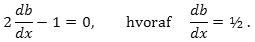Descartes undersøgelse af regnbuen

Lad os starte denne beskrivelse med et fantastisk billede af en regnbue. Når man står og kigger på en regnbue, har man altid Solen i ryggen. Centrum for den cirkelformede regnbue ligger modsat Solen på himmelkuglen, så man kan højst se en halvcirkel af regnbuen; og en halvcirkel kan man kun se ved solopgang eller solnedgang. Og det er det, billedet viser:

'Fuldkommen' regnbue nær Brovst i Nordjylland den 20/6 2008. Foto: Anders Kvist

Omkring 1267 målte Roger Bacon regnbuens vinkelstørrelse. Han fandt, at vinklen mellem en solstråle og sigtelinjen til et punkt på regnbuen er 42°. Hvis Anders Kvist havde målt vinkelafstanden mellem de to ender af hans regnbue ville han have fundet, at den var 84°. En teoretisk beregning af dette tal kræver kendskab til brydningsloven. Den blev fundet af Snell i 1621 og lidt senere, men uafhængigt af Snell, af Descartes. På den baggrund lykkedes det for Descartes at beregne de 42°. Jeg kender ikke Descartes beregningsmetode. Her bruger jeg differentialregning, som Descartes ikke kendte. Midt i 1600 - tallet kendte man ikke differentialregning, men man havde specielt tilpassede metoder til løsning af problemer, som vi i dag vil sige kræver differentialregning. Descartes kendte ikke til, at forskellige farver lys brydes lidt forskelligt. Det vender vi tilbage til under Newton. I det følgende tænker vi os, at lyset er hvidt, og at det brydes ensartet.

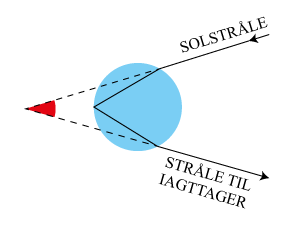Vi starter med at gætte på, at regnbuen dannes, når lys brydes i en vanddråbe på den symmetriske måde, som er vist på figuren til venstre. Lyset brydes to steder og det reflekteres i nogen udstrækning fra dråbens bagvæg. Det er et lidt frækt gæt, men vi prøver. Når det ellers er tåge eller regnvejr og samtidig solskin, så vil lyset ramme alle mulige regndråber, og det vil blive kastet tilbage i en masse forskellige retninger, afhængigt af indfaldsvinklen. Hvad skal der til, før der dannes en regnbue? Et nærliggende gæt vil være, at der skal være totalreflektion ved dråbens bagvæg, men det gæt fører ikke til noget. Her kommer så Decartes uventede gæt:

En enkelt lysstråle s gør intet nævneværdigt indtryk på øjet. Der skal være et bundt af lysstråler lige ved siden af s, der bliver brudt lige så meget som s, og som derfor rammer øjet som et parallelbundt.

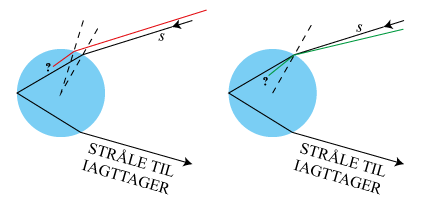
Situationen er vist på figuren til venstre. Det er vores ønske, at den røde stråle skal forlade dråben i samme retning, som den sorte. Det viser sig imidlertid beregningsteknisk at være meget svært at styre. I stedet kigger vi på situationen til højre, hvor vi har gjort indfaldsvinklen for den grønne stråle en smule større, end den er for den sorte, lige som det var for den røde stråle til venstre. Igen ønsker vi at opnå, at den grønne og den sorte stråle forlader dråben i samme retning. Og denne gang kan beregningerne gennemføres.

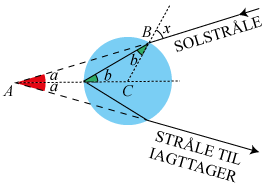Det skal med andre ord være sådan, at hvis man ændrer indfaldsvinklen x en lille smule, så ændres den samlede afbøjning på 2a ikke. Afbøjningen er en funktion af x, og det vi ønsker, er at finde en værdi af x, for hvilken da/dx = 0. Så nu kommer der lidt formeleksercits: Vinkelsummen i trekant ABC er a + x + (180° - 2b) = 180°, hvoraf a = 2b - x. Da da/dx = 0 fås heraf ved differentiation mht. x at

Hvis nu n = 1,3330 betegner brydningsforholdet ved overgang fra luft til vand, siger brydningslovn, at sinx = nsin b. Ved differentiation mht. x fås heraf, at

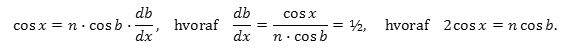
Ved kvadrering fås heraf, at

4cos²x = n²cos²b  eller 4(1 - sin²x) = n²(1 - sin²b) .

Da sinx = nsinb fås endelig, at

4(1 - n² sin²b) = n²(1 - sin²b),

altså en ligning til bestemmelse af b. Man får videre, at

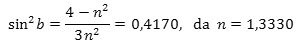
Heraf fås, at b = 40,2246°, og af formlerne ovenfor fås så, at x = 59,4104° og 2a = 42,0776°, i fin overenstemmelse med Roger Bacons bestemmelse af regnbuens størrelse. - Billedet nedenfor kunne passende illustrere Descartes begejstring, da han var nået frem til dette resultat.

På billedet kan man ane 2 stykker af en anden regnbue, der er større end den tydelige. Den regnbues størrelse kan beregnes på tilsvarende måde, når man inde i dråberne bruger en anden strålegang, sådan som det er beskrevet under Theodoricus Dietrich.

Hvis du støder på et ord, hvis betydning du ikke kender, så søg på ordet.