Forside Søgning Liste

Fra Newtons og Leibniz´ tid blev to nye matematiske begreber af afgørende betydning i fysikken. De to begreber hedder differentiation og integration. Der var forløbere for dem allerede i græsk oldtid, men først i slutningen af 1600-tallet kom der nogenlunde styr på begreberne. Her prøver vi at forklare, hvad differentiation er for en størrelse.

1. Definition af differentialkvotient

Vi tager udgangspunkt i bestemmelse af tangenter til kurver, hvor differentiation tydeligt viser sig. Da begrebet er noget abstrakt, starter vi med nogle konkrete eksempler, først tangentbestemmelse for en parabel.

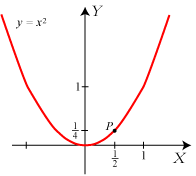
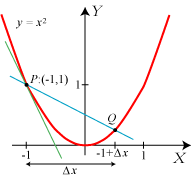
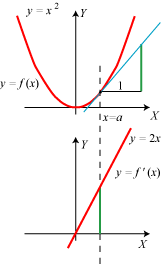
Vi starter med en parabel med ligningen y = x² og vælger som eksempel punktet P: (x,y) = (½,¼), der ligger på parablen. Vi vil finde en ligning for parablens tangent i punktet P. Så må vi først og fremmest definere, hvad en tangent er. En fysiker vil sige, at man skal tage et stykke af parablen, der indeholder P, og som er så lille, at det kan betragtes som et liniestykke. Parablens tangent er så den linie, der indeholder dette liniestykke. Her vil den skeptiske matematiker mumle "hvor lille", og det kan der selvfølgelig være noget om, men hvad skal man ellers sige?	Det, man ellers skal sige, er følgende. Vi vælger et andet punkt Q på parablen og kigger på linien gennem P og Q. Parablens tangent i P defineres så som den linie, linien PQ nærmer sig ubegrænset til, når Q langs parablen bevæger sig hen mod P. Den søgte tangent går gennem P. Det drejer sig derfor om at finde tangentens hældningskoefficient. 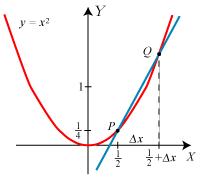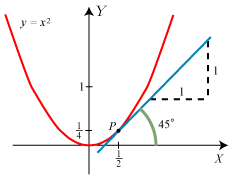Som vist på figuren tænker vi os, at vi kommer fra P til Q ved at ændre X-koordinaten fra ½ til 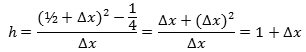½ + Δx. (Det sære navn "delta x" skyldes, at det er en differens mellem to x-værdier). Ved denne ændring ændres Y-koordinaten fra ¼ til (½ + Δx)². Heraf følger, at hældningskoefficienten for den blå linie er	Og så er vi næsten færdige. For når Q nærmer sig ubegrænset til P, vil Δx nærme sig ubegrænset til 0, og h nærmer sig derfor ubegrænset til 1. Tangentens hældningskoefficient er derfor 1, dvs. at tangenten danner en vinkel på 45° med X-aksen. Så nu har vi gennemført vores første tangentbestemmelse. Man siger, at h har grænseværdien 1, når Δx går mod nul, og skriver h→1 for Δx→0. Vi fandt en positiv tangenthældning. Det hænger sammen med, at for positive værdier af x vokser y, når x vokser.

Når Q på den midterste figur ovenfor nærmer sig ubegrænset P, vil Q også nærme sig koordinatsystemets begyndelsespunkt, men det vil ikke nærme sig ubegrænset til begyndelsespunktet. Så du må forstå, at ordet ubegrænset ovenfor er strengt nødvendigt. Når noget nærmer sig ubegrænset, kan det komme lige så nær, som man vil have det.

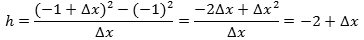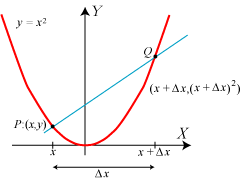
Vi gentager processen med et nyt punkt på den samme parabel. Vi vælger punktet P med koordinater (-1,1) og giver igen x en tilvækst Δx og når derved frem til parabelpunktet Q med koordinater (x,y) = (-1+Δx,(-1+Δx)²). Hældningskoefficienten for den blå korde PQ bliver så Da h→−2 for Δx→0, har den søgte grønne tangent hældningskoefficienten −2. Tangenten får derfor ligningen y = -2x-1, hvor det sidste −1 er bestemt ved, at punktet (−1,1) skal passe i ligningen. Læg mærke til, at y = 0, når x = -½, altså halvdelen af x-koordinaten for P. Sådan er det hver gang, når det er en parabel, man kigger på. Denne gang fik vi en negativ hældningskoefficient. Det hænger sammen med, at for negative værdier af x aftager y, når x vokser.

Nu håber vi så, at læseren er moden til at tage det afgørende skridt, nemlig at bestemme hældningskoefficienten for tangenten til den sædvanlige parabel i et vilkårligt parabelpunkt P:(x,y). Hældningskoefficienten for den blå korde bliver denne gang

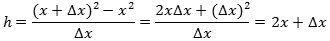
Da h→2x for Δx→0, har den søgte tangent hældningskoefficienten 2x. Hvis man vil opskrive ligningen for tangenten, er man nødt til at omdøbe koordinaterne til P, f.eks. til P:(x_o,y_o). I dette punkt bliver hældningskoefficienten til tangenten 2x_o, og tangentens ligning bliver derfor

Nu er vi så nødt til at sige lidt om begrebet en funktion. Et udtryk som y = x ² kaldes for en funktion, og man siger, at y er en funktion af x. Det er her afgørende, at der for en opgiven x-værdi kun findes én y-værdi. Parablen kaldes så funktionens graf eller dens grafiske billede. Andre eksempler på funktioner er y = sin x, y = 2x+3 og y = 1/x. En cirkel er ikke det grafiske billede af en funktion, fordi det sker, endda tit, at der til en given værdi af x svarer to y-værdier. Man taler derimod stadig om en funktion, selv om der er x-værdier, som der ikke svarer nogen y-værdi til. F.eks. er y = √x en funktion, selv om man ikke kan tage kvadratroden af et negativt tal. Standardnavnet for en funktion er f (x). Dette navn blev indført af Euler i 1734, så det har holdt sig godt. Nulfunktionen er 0 for alle værdier af x, og en konstant funktion har samme værdi for alle værdier af x. Et polynomium er et udtryk som 3x⁵+7x⁴ − x² + 4x + 7. Dette polynomium er af 5. grad.

Ovenfor så vi, at der til funktionen y = x² hører en anden funktion, nemlig funktionen y = 2x, sådan at værdien af den anden funktion for x = a er hældningskoefficienten for tangenten til grafen for den første funktion i det punkt, der har x = a. De to grønne liniestykker på figuren er altså lige lange, ligemeget hvor den lodrette punkterede linie er tegnet. Hvis den øverste funktion betegnes f (x), kaldes den nederste f ´(x), man siger f-mærke x. f ´(x) kaldes for differentialkvotienten af f (x) eller den afledede af funktionen f (x).

Her kommer så den formelle definition af differentialkvotienten for en funktion: Når f (x) er en funktion, defineres dens differentialkvotient f ´ (x) ved at Den geometriske betydning af f ´ (x) er, at f ´ (x) er hældningskoefficienten for den grønne tangent til grafen for funktionen f (x) i punktet med abscissen x.

Den lange brøk ovenfor kaldes differenskvotienten, både tæller og nævner er jo differenser. Man plejer at give tælleren navnet Δy, og så kan relationen ovenfor skrives på den simplere form

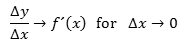
Differentialkvotienten er altså grænseværdi for differenskvotienten, og denne skrivemåde har inspireret til navnet dy/dx for differentialkvotienten, altså

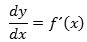
Skrivemåden er historisk betinget. I differentialregningens barndom opfattede man nemlig dx som en fantastisk lille x-tilvækst og dy som den tilsvarende også fantastisk lille y-tilvækst. Og så tænkte man sig, at forholdet mellem disse to tal var et ganske almindeligt tal, nemlig funktionens differentialkvotient. F.eks. er 0,00000000006 og 0,00000000003 fantastisk små tal, men deres forhold er det ganske almindelige tal 2. dx og dy kaldtes differentialer, og så er det jo helt logisk at det hedder en differentialkvotient. Hvis man forfølger denne tankegang, og skriver den sidste formel på formen dy = f ´ (x)dx, kan man se, at f ´(x) angiver, hvor mange gange hurtigere y vokser hurtigere end x i omegnen af punktet x. Man bruger også navnet y´ om differentialkvotienten til en funktion y.

Funktionen f (x) har altså differentialkvotienten f ´ (x). Denne funktion har også en differentialkvotient f ´´(x). Den kaldes den anden afledede af  f (x), og således kan man få afledede af vilkårlig høj orden. Hvis man starter med et polynomium af n-te grad, vil de afledede af orden større end n alle være nulfunktionen.

2. Nogle vigtige differentialkvotienter

• Den lineære funktion y = ax+b har differentialkvotienten y´ = a. Grafen er jo en ret linie med hældningskoefficient a
• Funktionen y = xⁿ har differentialkvotienten y´ = n·xⁿ⁻¹
• Funktionen y = √x har differentialkvotienten 1/(2√x). Bevis: Vi skal kigge på brøken
  
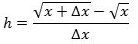
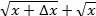  men her går både tæller og nævner mod 0 for Δx→0, og så kan man ikke sige, hvad brøken går mod. Det hjælper imidlertid, hvis man forlænger brøken med , for så får man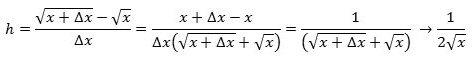 Vi har altså fundet, at Resultatet svigter, når x = 0. I det tilfælde har kvadratrodsfunktionen lodret tangent, og den har jo ingen hældningskoefficient.
• Funktionen y = sin x har differentialkvotienten y´ = cos x. Dette kræver, at x er et radianmål.
• Funktionen y = cos x har differentialkvotienten y´= -sin x. Dette kræver, at x er et radianmål.
• Funktionen y = e^x har differentialkvotienten y´= e^x
• Den naturlige logaritmefunktion y = ln x har differentialkvotienten y´= 1/x, x>0

Der gælder en række regneregler for differentialkvotienter. De vigtigste er opført i nedenstående tabel, hvor a og k betegner konstanter, altså uafhængige af x:

Den næstsidste regel er et specialtilfælde af den sidste. Som et vigtigt eksempel nævner vi, at når y = sin ωx, er y´ = ω·cos ωx, og y´´ = −ω²·sin ωx.

Når y = cos ωx, er y´ = −ω·sin ωx, og y´´ = −ω²·cos ωx.

Det følger af disse to resultater, at funktionen

opfylder ligningen y´´ = −ω²·y, lige meget hvilke værdier af a og b man vælger. Man kan bevise, at der ikke er andre funktioner end disse, der opfylder ligningen y´´ = −ω²·y. Ligninger af denne type, hvor den ubekendte er en funktion, og hvor den ubekendte y optræder sammen med en eller flere af differentialkvotienterne y´, y´´, ... kaldes differentialligninger. De er tit svære at løse. Der er skrevet mange tykke bøger om differentialligninger.

3. Maksimum og minimum

På figuren til højre viser vi det grafiske billede af en funktion y = f(x). Funktionen har et minimum for x = x1 og et maksimun for x = x2. I disse to punkter har funktionen vandret tangent, så f ´(x1) = 0, og f ´(x2) = 0. Derfor kan man finde en funktions maksima og minima ved at finde nulpunkter for differentialkvotienten. Der kan også være vandret tangent i et punkt, hvor der hverken er maksimum eller minimum. Hvis man er i tvivl, kan man afgøre det med nogle støttepunkter. Nedenfor viser vi et eksempel på bestemmelse af maksimum og minimum.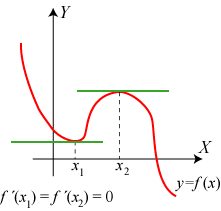

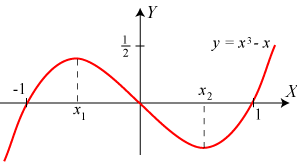Vi betragter funktionen y = x3 - x. Dens graf er tegnet ved hjælp af støttepunkter på figuren til venstre. Det er tydeligt at se, at der er et maksimum og et minimum. For at finde deres beliggenhed og størrelse differentierer vi funktionen. Differentialkvotienten er y´ = 3x2 - 1, og den er 0 for x = ±1/√3 = ±0,58. Der er maksimum for x = x1 = - 0,58, og maksimumsværdien udregnes til 0,38. Der er minimum for x = x2 = 0,58, og minimumsværdien udregnes til - 0,38. Vi viser en anvendelse af metoden i fysik under 1657 Fermat.

Hvis du støder på et ord, hvis betydning du ikke kender, så søg på ordet.