Forside Søgning Liste

Indtil 1600-tallet havde man i de forskellige kulturer kun tilfredsstillende enheder for længde, vinkler og vægt. Ved hjælp af længdeenheden kunne man definere enheder for areal og rumfang. De for fysikken vigtige størrelser tid og temperatur kunne kun måles med ringe nøjagtighed. De europæiske ure havde f.eks. ingen minutviser, og termometrene havde ingen (fælles) gradskala. I begyndelsen af 1600-tallet var der en voksende forståelse blandt fysikerne i Europa for, at man i fysikken skal bruge målinger baseret på veldefinerede enheder for de forskellige fysiske størrelser. Disse enheder for f.eks. tid, længde, areal, vægt, kraft og varmegrad kaldes dimensioner.

Der er to slags enheder:

• Der er først de enheder, der er defineret ved en bestemt standard. De kaldes grundenheder. De kan i forskellige sammenhænge vælges lidt forskelligt. Her vil vi benytte enhederne for længde, masse, tid og temperatur som grundenheder. I CGS-systemet benyttes enhederne cm, gram, sekund og grad som grundenheder, og i SI-systemet bruges m, kg, sek og grad. Man bruger betegnelserne L, M, T og G for disse grundenheder og kalder dem dimensioner, f.eks. har længde dimensionen L. Det ligger lidt specielt med vinkelmåltal. Hvis man skal bestemme en vinkels måltal i radianer, skal man tegne en cirkelbue mellem benene med centrum i toppunktet. Radiantallet for vinklen er så forholdet mellem buens længde og cirklens radius. Da dette forhold er uafhængigt af den valgte længdeenhed, er radianmålet dimensionsløst. Det samme gælder principielt gradmåltallet, men selvfølgelig må man gøre opmærksom på, hvilket af de to måltal man vælger.
• Den anden type af enheder er afledte af grundenhederne. F.eks. måles hastighed i cm/sek, og man siger derfor, at hastighed har dimensionen LT^-1. Dette afspejler, at en hastighed bestemmes ved, at man dividerer en længde med en tid. Tilsvarende måles acceleration i enheden cm/sek², og acceleration har derfor dimensionen LT^-2. En acceleration bestemmes jo ved, at man dividerer en hastighedstilvækst med en tid. Massefylde måles i gram pr kubikcentimeter, altså i g/cm^-3, og den har dimensionen ML^-3. Længdeudvidelseskoefficienten for et stof defineres som udvidelsen målt i cm pr grads opvarmning og pr cm stang af stoffet. Længdeudvidelseskoefficienten måles derfor i cm/(grad·cm) = grad^-1. Dimensionen er altså G^-1. At L ikke indgår i dimensionen afspejler, at længdeudvidelseskoefficienten beholder sin talværdi, hvis man i definitionen (begge steder) anvender en anden længdeenhed end cm.

Lad os betragte et legeme, der drejer sig om en akse. Lad os sige, at legemet i et bestemt tidsinterval af længden T drejer sig en vinkel v. Hvis forholdet ω = v/T er det samme for alle tidsintervaller, siger man, at legemet drejer sig med konstant vinkelhastighed ω. Da v er dimensionsløs, bliver enheden for vinkelhastighed sek^-1. Dimensionen er altså T ^-1. Men hvis vinkelhastigheden f. eks. er 7 sek^-1, er man nødt til at oplyse, om vinklen er målt i grader eller radianer. I teoretisk fysik bruger man næsten altid radianer, men i praksis kan man godt se en vinkelhastighed angivet til 7 grader/sek.

Der er flere fordele ved at regne med enheder på den beskrevne måde:

1. Det er en fordel ved den anvendte skrivemåde, at det bliver meget overskueligt, hvis man ønsker at skifte enhed. F. eks. er

   72 km/time = 72 (1000 m)/(3600 sek) = 72.000/3600 m/sek = 20 m/sek.

2. En anden fordel er, at hvis man under en udregning hele tiden tager enhederne med, så vil man opdage visse typer af regnefejl. Hvis man f.eks. undervejs glemmer en division, kan man ende med en acceleration, der måles i cm/sek. Hovsa, siger man så, jeg må have glemt en division med en tid.

3. En tredie fordel er, at hvis man ikke rigtigt kan komme i tanke om en formel, så kan en dimensionsbetragtning lette på sagen. Lad os f.eks. sige, at en partikel bevæger sig med hastighed v rundt på en cirkel med radius r, og man ønsker at finde størrelsen w af accelerationen og ikke rigtig kan huske formlen, så kan man gå sådan frem: v måles i cm/sek, r måles i cm, og resultatet skal være i cm/sek². For at få sek² nede i nævneren er man nødt til at kvadrere v, men så bliver der cm² oppe i tælleren, og det 2-tal kan man få væk ved at dividere med r, så mon ikke formlen er
   
   

   

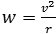
   I dette tilfælde er det svært at finde et andet udtryk i r og v, der har den rigtige dimension, og formlen er faktisk rigtig. Dimensionsbetragtningen kan ikke oplyse, om der f.eks. skulle have stået 2π foran brøkstregen.

Betydningen af at vælge fornuftige enheder illustreres godt ved nedenstående eksempel:

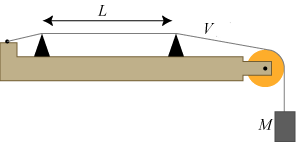
Omkring 1635 fandt Marin Mersenne ud af, at den mindste frekvens f, som strengen på figuren ovenfor kan svinge med, afhænger således af de variable på figuren ovenfor:

1. f er omvendt proportional med L. Det betyder, at hvis man gør L dobbelt så stor, bliver f halvt så stor.
2. f er proportional med kvadratroden af M. Det betyder, at hvis man gør M fire gange så stor, bliver f dobbelt så stor.
3. f er omvendt proportional med kvadratroden af vægten V af en længdeenhed af strengen. Det betyder, at hvis man gør V fire gange så stor, så bliver f halvt så stor.

Mersennes resultater er korrekte. De kan sammenfattes i formlen

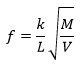
Her betyder k et tal, som man kan bestemme ved at måle ét sæt sammenhørende værdier af de 4 variable. k viser sig at afhænge af de enheder man angiver de variable i. Måske finder man, at k = 27,348, og det kan man jo ikke sige andet end Nå- til. På Newtons tid ville en fysiker nok komme med den kommentar, at M egentlig burde erstattes med M·g, hvor g betyder tyngdeaccelerationen. Det er jo en kraft, der påvirker svingningstiden. Vægten V skal ikke erstattes med en kraft, det er massen, der spiller en rolle for svingningen. Formlen for frekvensen bliver nu

(*)                     

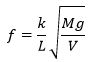
For nu at finde ud af, hvilen enhed k måles i, erstatter vi som ovenfor i formlen hver variabel med dens navn:

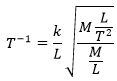
Her går de to M-er ud mod hinanden, og kvadratroden af de T^-2, der står under rodtegnet, bliver T ^-1, og det går ud mod T ^-1 på venstre side. På lignende måde ser man, at L-erne går ud mod hinanden, og heraf følger så, at k er dimensionsløs, altså uafhængig af de enheder man bruger. k kan så være et eller andet mærkeligt tal som 7,628 eller det kan være √3 eller det kan være 2π. Værdien af k kan man finde på to måder: Man kan indsætte sammenhørende værdier af alle de variable. Så får man noget i retning af k = 0,4999. Eller man kan teoretisk beregne værdien af k. Det lykkedes først hen mod år 1800, og man fandt så, at k = ½. Frekvensen bestemmes altså af formlen

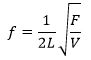
hvor F er den kraft, som strengen spændes ud med.

Når man skal lægge to fysiske størrelser sammen, eller blot sammenligne dem, skal de have samme dimension. Man kan som bekendt ikke afgøre, om Rundetårn er højere end et tordenskrald. Derimod kan man multiplicere og dividere størrelser med forskellig dimension.

Hvis du støder på et ord, hvis betydning du ikke kender, så søg på ordet.