|
Forside
Søgning
Liste |  |
Galileo Galilei
1. Inertiens lov
Fra Oldtiden og op mod Galileis tid var det en almindelig antagelse, at hvis et legeme bevæger sig,
da er det, fordi der er en "kraft", der driver legemet fremad. Hvis der ingen kraft er, går legemet i
stå, det mister sin impetus. Dette synspunkt, der stammer fra Aristoteles, understøttes
af mange dagligdags erfaringer. Bl.a. derfor var det et afgørende skel i fysikkens historie at erkende,
at det faktisk forholder sig modsat. Galilei var vist den første, der eksplicit formulerede
| Inertiens lov: Et legeme beholder sin hastighed i størrelse og retning med mindre "noget" udefra påvirker legemet. |
Dette "noget" kan f.eks. være gravitation, gnidning eller påvirkning fra en fjeder. I dag kalder vi det "kræfter", men dette begreb var endnu på Galileis tid uklart. Cusanus var vist den, der før Galilei var nærmest ved at formulere inertiens lov. I sine astronomiske overvejelser antog Galilei, at en jævn cirkelbevægelse også er en inertialbevægelse, der fortsætter uden at der er ydre kræfter, der vedligeholder hastigheden. Og det er jo heller ikke helt forkert: Gravitationen vedligeholder ikke hastigheden, den gør banen krum.
Formuleringen ovenfor bruger ordet "legeme". Egentlig burde der stå "partikel", dvs "lille legeme". Et legeme, der roterer, har jo ingen veldefineret hastighed. Galilei indså, at inertiens lov kan være yderst vanskelig at påvise eksperimentelt, fordi uvedkommende kræfter, især gnidning og gravitation, hele tiden ændrer bevægelsestilstanden.
Lad os nævne et godt (men moderne) eksempel på eksperimentel iagttagelse af inertiens lov: Hvis man i
et tog, der kører 100 km/t, kaster en bold op i luften, kan man gribe den igen efter ½ sekunds forløb,
uden at
man behøver at flytte sig. Og det på trods af, at toget på det halve sekund har bevæget sig 15 meter
fremad. Ud over de lodrette bevægelser har bolden nemlig også i luften beholdt togets fremadrettede
hastighed. Galilei nævner et tilsvarende eksempel, nemlig et legeme der, fra toppen af masten på et
skib i fart, falder ned på dækket lige ved siden af masten.
2. Ulige tunge legemer falder lige hurtigt.
Galilei gjorde også op med en anden af Aristoteles fejltagelser: Aristoteles påstod, at når et
legeme vejer dobbelt så meget som et andet, så falder det dobbelt så hurtigt. Det er ret
uforståeligt, at Aristoteles og hans efterfølgere kunne tro sådan. Man kan nemlig tænke sig til, at
det er forkert.
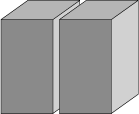
Figuren viser to ens jernklodser. Hvis vi giver slip på dem samtidig og lader dem falde, følges
de ad, da de er ens. Men så kan det ikke gøre nogen forskel, om de er limet sammen på de to flader, der
vender mod hinanden. Det tunge sammenlimede legeme falder altså lige så hurtigt som et med den halve vægt!
Det er meget mærkeligt, at Aristoteles kunne hævde, at den sammenlimede klods falder
dobbelt så hurtigt som de to enkelte klodser. Galilei supplerede pricipielle overvejelser af denne art
med eksperimenter. Galileis elev Vicenzo Viviani beretter nemlig, at Galilei lod legemer med forskellig
vægt falde samtidig fra det Skæve Tårn i Pisa og så, at de nåede jorden samtidig. Galilei
var klar over, at man skulle sørge for, at luftmodstanden ikke kommer til at spille en afgørende rolle.
Det sørgede han for ved at benytte legemer med stort forhold mellem vægt og overflade. Et stykke papir
eller f.eks. en fjer duer ikke. De har alt for stor overflade i forhold til vægten. Efter at
luftpumpen blev opfundet, har man konstateret, at i et lufttomt rum falder en fjer og et blylod
lige hurtigt. I det følgende ser vi bort fra luftmodstanden.
3. Hvordan foregår det frie fald?
Nu kommer vi til det vigtigste af Galileis resultater. Når nu Galilei havde fundet ud af, at alle legemer falder lige hurtigt var det naturligt for ham at prøve at finde ud af, hvor hurtigt de falder. Det er en kendt erfaring, at jo højere oppefra et legeme falder, jo mere ondt gør det at få det i hovedet. Faldende legemer bevæger sig altså hurtigere og hurtigere. Men at komme videre herfra var på Galileis tid meget vanskeligt. De to vigtigste vanskeligheder var, at uret ikke var opfundet, og at faldet foregår så hurtigt, at det med den tids hjælpemidler var umuligt at måle sammenhørende værdier af faldtid og faldvej. Begreberne hastighed og acceleration var heller ikke klart defineret på den tid. Også i dag er disse to begreber vanskelige at definere, selv for en retlinet, men uregelmæssig bevægelse.
Galilei startede med en række teoretiske overvejelser. Vi holder et legeme i hånden, og
på et tidspunkt giver vi slip på det og lader det falde. Legemet starter i hvile, altså med hastighed 0.
Ifølge inertiens lov må der så være en ydre påvirkning, der ændrer hastigheden. Denne ydre påvirkning er
gravitationen, der hænger sammen med legemets vægt. Den får åbenbart legemet til at bevæge sig hurtigere
og hurtigere. Galilei antog nu, at dette foregår på den måde, at legemet i hvert sekund får samme
hastighedstilvækst. Idag ville vi sige, at han antog, at legemet bevæger sig med konstant acceleration,
idet accelerationen er hastighedstilvæksten pr. sekund. Det er på ingen måde indlysende, at antagelsen er
korrekt, men det er vel naturligt i første omgang at antage, at det forholder sig sådan, og så se
hvad det fører til.
4. En matematisk model
Vi løsriver os nu midlertidigt fra det frie fald og går over til en teoretisk betragtning.
Vi tænker os en partikel, det til tidspunktet
t = 0 starter med at bevæge sig på en ret linie med konstant acceleration. For t = 0
er hastigheden 0 og lad os betragte det konkrete tilfælde, hvor accelerationen g hele tiden er
g = 10 m/sek².
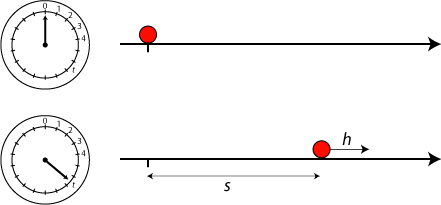
Da hastigheden øges med 10 m/sek hvert sekund, er partiklens hastighed h efter t
sekunders forløb h = 10·t m/sek. Den tilbagelagte vejlængde s efter t
sekunders forløb kan umiddelbart bestemmes ved hjælp af "middelhastighedssætningen", se 1330
Merton College. Middelhastighedssætningen siger, at vores legeme kommer lige så langt, som hvis det i
t sekunder bevæger sig med hastigheden ½(0 + 10t). Vejlængden s bestemmes altså af
formlen s = ½t·10t = ½·10·t². På samme
måde kan man naturligvis indse, at hvis den konstante acceleration er g m/sek² i stedet for
10 m/sek², da bestemmes hastigheden og vejlængden efter t sekunders forløb af formlerne
h = g t og s=½ g t². Resultatet er, at Galilei beviste
følgende sætning:
| Hvis et legeme bevæger sig på en ret linie med konstant acceleration g i t sekunder,
og hvis det
starter med hastighed 0, da bestemmes hastigheden h og den tilbagelagte vejlængde s af
formlerne
h = g t og s=½ g t² |
Det afgørende i beviset er brugen af middelhastighedssætningen. Vi ved ikke, om Galilei kendte dette resultat fra Merton College. Vi gætter på, at det gjorde han ikke, og at han i stedet selv beviste den. I dag beviser man formlen for s ved hjælp af integralregning, men den var ikke opfundet på Galileis tid. Vi ved ikke, hvordan Galilei og fysikerne på Merton College beviste den.
Af formlerne ovenfor kan man udlede følgende formel for hastigheden udtrykt ved vejlængden:
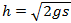
Vi slutter dette afsnit med en animation, der viser hvordan en bevægelse med konstant acceleration kan se ud:
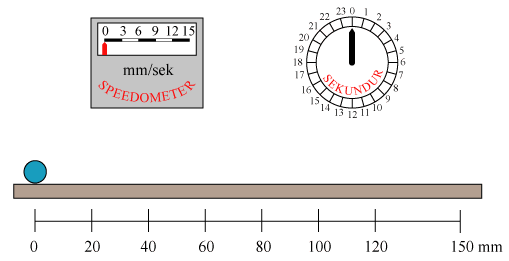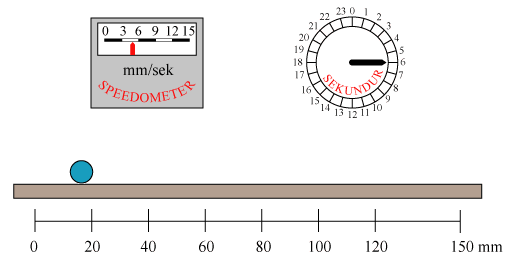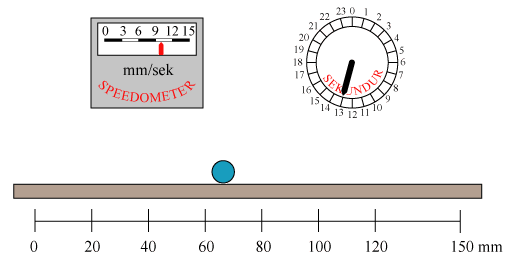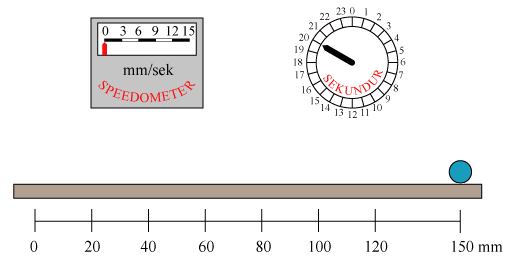
Den blå kugle bevæger sig med konstant acceleration. Det kan man se på speedometret, hvor den røde viser bevæger sig med konstant fart. Hastighedstilvæksten er altså den samme i to vilkårlige lige lange tidsintervaller. Hastigheden stiger på 20 sekunder fra 0 mm/sek til 15 mm/sek, så accelerationen (dvs hastighedstilvæksten pr. sekund) bliver g = 15/20 = 0,75 mm/sek2. Skrivemåden mm/sek2 betyder mm/sek pr. sekund, og den fortæller også, at en acceleration bestemmes ved, at man to gange dividerer en en længde med en tid. I vores tilfælde sådan: Først finder man (dvs speedometret) sluthastigheden ved at dividere vejlængden i et kort tidsinterval, lige før der er gået 20 sekunder, med tidsintervallets længde. Det giver så de 15 mm/sek. Og så dividerer man hastighedstilvæksten med 20 sekunder, så får man accelerationen. Hvis man vil finde kuglens fart i det øjeblik den passerer 100 mm stregen, kan man benytte formlen ovenfor. Man finder, at 2gs =2·0,75·100 = 150 mm2/sek2. Hastigheden fås så ved at man tager kvadratroden, så h=12,25 cm/sek. Det passer med, hvad man kan aflæse på speedometret.
5. Faldloven og skråplanet.
Efter disse teoretiske overvejelser skulle det nu helst være muligt at undersøge, om det frie
fald foregår med konstant acceleration. Som før nævnt var det ikke let dengang, fordi faldhastigheden
hurtigt bliver meget stor. Galilei fik så den ide at benytte Stevins resultat om skråplanet til, om
man så må sige, at formindske tyngdekraften.
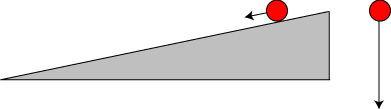
Stevin fandt ud af, at når den skrå side af et skråplan er f.eks. 5 gange så langt som højden,
da trækker tyngden en kugle på skråplanet ned i skråplanets retning med en styrke, der kun er en
femtedel af kuglens almindelige vægt. Ved at variere på skråplanets hældning kunne Galilei derfor opnå
en så stor reduktion af tyngdekraften, som han ville, og derved opnå målbare tider og vejlængder.
Som ur anvendtes en af de tilstedeværendes puls og ved andre lejligheder et pendul. Billedet nedenfor
viser en situation under udførelsen af
et forsøg.
 |
Frescoen er af Giuseppe Bezzuoli. |
Skråplansforsøgene viste, at de tilbagelagte vejlængder stemte fint overens med den teoretisk udledte formel s = ½ g t² med en værdi af g, der med ovennævnte skråplanshældning var ca 2 m/sek². Så accelerationen ved det lodrette fald må være ca 10 m/sek². Den korrekte værdi som man kender i dag er 9,807 m/sek² eller 980,7 cm/sek². Denne acceleration kaldes tyngdeaccelerationen, og den betegnes g efter ordet gravitation.
Antagelsen, om at accelerationen er konstant, lod sig ikke umiddelbart kontrollere ved et eksperiment. Men
Galilei viste, at antagelsen har den matematiske konsekvens, at den tilbagelagte vejlængde
bestemmes af formlen s=½ g t², og det viste sig så, at resultaterne af
skråplansforsøgene stemte fint med denne formel. Det var derfor naturligt at antage, at også det frie fald
foregår med konstant acceleration. Denne form for samarbejde mellem matematik og virkelighed
blev forbillede for mange fysikere i tiden efter Galilei.
6. Fald med lodret begyndelseshastighed
På baggrund af det foregående er det ikke vanskeligt at finde ud af, hvad der sker, hvis faldbevægelsen
starter med en hastighed v forskellig fra 0. Mere generelt betragter vi en partikel, der i t sekunder
bevæger sig på en ret linie med konstant acceleration g, og vi antager yderligere, at legemet i
startøjeblikket har hastigheden v i liniens retning
| Hvis et legeme i t sekunder bevæger sig på en ret linie med konstant acceleration g,
og hvis det
starter med en hastighed v i liniens retning, da bestemmes hastigheden h og den tilbagelagte vejlængde
s efter t sekunders forløb af
formlerne
h = v + gt og s = vt +½ gt² |
Egentlig skal linien være orienteret, dvs have en pil i den ene ende, og så skal h, v og g regnes negative, hvis de går mod pilretningen.
Resultatet følger af en opdagelse af Galilei, som i dette tilfælde siger, at den resulterende hastighed og vej fås ved addition af de bidrag, som tyngden og begyndelseshastigheden hver for sig giver. Vi kunne kalde det superpositionsprincippet. Det er det samme princip, som vi benyttede ovenfor, da vi skrev om boldspilleren i et kørende tog. Princippet foregriber reglen om kræfternes parallellogram. Det er et afgørende fremskridt i bevægelseslæren.
7. Kasteparablen
Superpositionsprincippet er også afgørende for, at det efter årtusinders forgæves forsøg endelig lykkedes for Galilei at bestemme den
banekurve, som beskrives af et legeme, der kastes skråt op i luften. Vi starter med det specielle tilfælde, hvor begyndelseshastigheden
går i vandret retning, sådan som det er vist på figuren nedenfor.
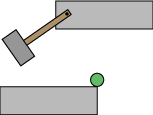
Vi vil finde ud af, hvordan den grønne kugle vil bevæge sig, hvis vi lader hammeren falde. Lad os sige, at hammeren giver
kuglen hastigheden v ; den går i vandret retning. Vi lader
g betegne den acceleration, som tyngden giver kuglen.
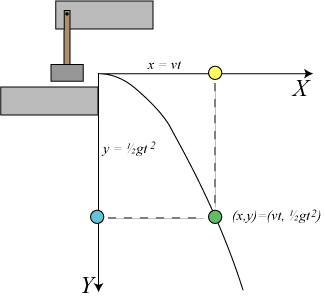
Vi bruger nu superpositionsprincippet. Den grønne kugle udfører samtidig to bevægelser:
1. Som følge af hammerslaget udfører kuglen en vandret, jævn bevægelse med hastighed v. Så vil den t sekunder efter start være nået til den gule position nået. Kuglen har bevæget sig afstanden vt i vandret retning.
2. Kuglens tyngde giver kuglen en bevægelse lodret nedad med begyndelseshastighed 0 og konstant acceleration g. Efter t sekunders forløb har den tilbagelagt vejen ½gt² og har nået den blå position.
Superpositionsprincippet siger så, at i det XY-koordinatsytem, der er vist på figuren, har den grønne kugle efter t sekunders forløb koordinaterne
(x,y) = (vt, ½gt²)
Af udtrykket for x fås, at t = x/v. Indsættes dette i udtrykket for y fås, at
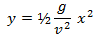
Denne ligning fremstiller en parabel, så resultatet er, at den grønne kugle bevæger sig på en (halv) parabel.
Til sidst i dette afsnit vil vi bestemme banekurven for et legeme, der kastes skråt op i luften.
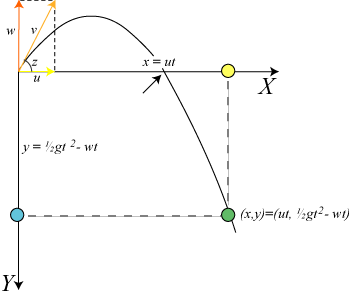
Vi tænker os ,at legemet (den grønne kugle) starter i koordinatsystemets begyndelsespunkt med en starthastighed v. Hvis der ikke var nogen tyngde, ville legemet fortsætte i v´s retning og med konstant fart. Vi bruger nu superpositionsprincippet omvendt, og forestiller os, at denne jævne bevægelse fremkommer ved, at legemet (den gule kugle) bevæger sig ud ad X-aksen ned hastighed u og samtidig op ad Y-aksen med hastighed w. Alt i alt har vores legeme nu dels en bevægelse i X-aksens retning med hastighed u, og dels en bevægelse i Y-aksens retning (den blå kugle) med begyndelseshastighed w og acceleration g rettet nedad. Til tidspunktet t har legemet derfor koordinaterne
(x,y)=(ut,- ½gt2 + wt)
Når t varierer, mens u, w og g er faste talværdier, fremstiller denne formel en parabel med ligningen
y= - ½g(x/u)2 + wx/u
Lad os illustrere resultatet med et konkret eksempel. Vi vælger v=1 cm/sek og w=½ cm/sek, og for at få noget, der ikke går alt for hurtigt, sætter vi g=0,2 cm/sek2. Det betyder, at hastigheden ved et frit fald øges med 0,2 cm/sek hvert sekund. Ifølge resultatet ovenfor har den grønne kugle til tidspunktet t koordinaterne
Figuren nedenfor viser situationen for t = 8.
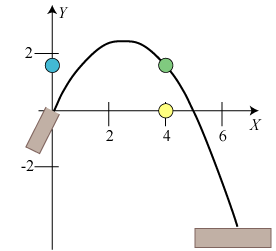
Den grønne kugle er skudt ud af kanonen til venstre,
og den gule og den blå kugle viser de to bevægelser, som ved superposition giver den grønne kugles bevægelse.
Animationen nedenfor viser bevægelsen i tidsintervallet 0 < t < 13.
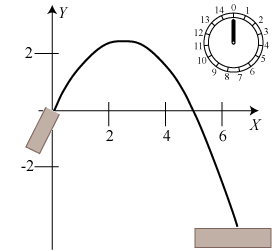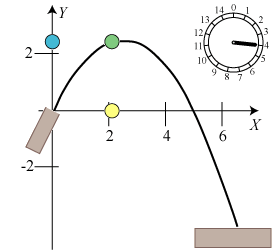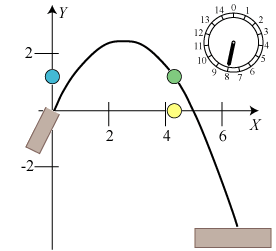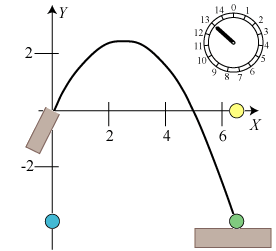
Vi har ovenfor ikke alene vist, at banekurven bliver en parabel, vi har også fundet en formel, som man kan bruge, hvis man vil besvare
spørgsmål om kastebevægelsen. Lad os give et eksempel fra ballistikken: Hvilken hældning skal en kanon have, hvis man vil skyde så langt som muligt
på en vandret flade? Skudvidden er x-koordinaten til det punkt, som den sorte pil på figuren peger på. Men der er y
=0, altså ½g(x/u)2 - wx/u=0, hvilket - ud over x= 0 - giver skudvidden
x = 2uw/g
Men her er u = v cos z og w = v sin z, så skudvidden bliver
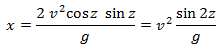
og det er jo maksimalt for z = 45°, et resultat der ikke er særlig overraskende, men man kunne jo aldrig vide! Resultatet blev fundet af Tartaglia i 1546, og Galilei viste så senere, at det kunne udledes af hans faldlove.
I dag synes vi, at det var simple overvejelser, der førte frem til resultaterne, og det kan være svært at forstå, at der skulle så mange forgæves forsøg til, før det lykkedes. Se under kastebevægelsen.

8. Pendulbevægelsen
Et pendul er et lille legeme, der hænger i en snor, der sidder fast opadtil. Hvis man fører pendulet ud til siden og slipper det, vil det svinge frem og tilbage. Den tid, pendulet bruger til at bevæge sig fra en yderstilling til det igen er i samme yderstilling, kaldes pendulets svingningstid. Det er en kompliceret sag at beskrive pendulers bevægelse. Det fortælles, at Galilei kom igang med at undersøge pendulbevægelser ved at opdage, at to forskellige lysekroner, der hang lige langt ned fra loftet i Pisas domkirke, svingede i takt.
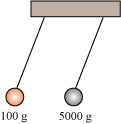 | Galileis første resultat om penduler var, at to lige lange penduler med forskellige masser har samme svingningstid - hvis man ellers kan se bort fra luftmodstanden. Resultatet er let at efterprøve ved forsøg. Ved første blik kan det måske virke overraskende. Man forstår det måske bedre, når man sammenligner med det frie fald: Hvis vi tager bolden og blykuglen i hænderne og slipper dem samtidig, følges de ad ned. Godt nok hiver tyngden mest i blykuglen, men den er jo også sværere at få igang, og de to ting ophæver præcis hinanden. - Sådan forholder det sig altså også med pendulet. |
Når en gummibold, der vejer 100 g, og en blykugle, der vejer 5 kg, hænger i lige lange snore, svinger de med samme svingningstid |
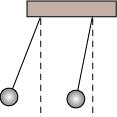 | Det næste Galilei undersøgte, var svingningstidens afhængighed af udsvingets størrelse. Også her er det let at lave forsøg, sådan som det er vist på figuren. Vi ved ikke, om Galilei kunne begrunde dette resultat teoretisk, det var ikke nogen simpel sag på Galileis tid. |
De to penduler er ens, men de er ikke ført lige langt ud til siden. Man ser så, at de overraskende nok svinger i takt alligevel, når man slipper dem samtidig |
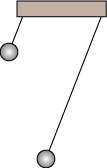 | Galilei undersøgte også, hvordan svingningstiden afhænger af snorlængden. Han fandt, at hvis man vil ændre et pendul, så det får k gange så lang svingningstid, så skal man bruge en snor, der er k² gange så lang. Svingningstiden er altså proportional med kvadratroden af pendullængden l. |
Det lange pendul er 4 gange så langt som det korte. Forsøg viser så, at det lange pendul har dobbelt så lang svingningstid som det korte. |
Resultatet af det hele er, at Galilei vidste, at
der findes et tal c, som kun afhænger af tyngdeaccelerationen g,
så svingningstiden T er c gange kvadratroden af l. Men han fandt ikke værdien af c. Senere
fandt man ud af, at svingningstiden bestemmes af følgende formel
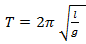
Her skal det være sådan, at hvis man f.eks. ønsker at måle længden i meter og tiden i sekunder, så skal tyngdeaccelerationen måles i meter pr. sekund i anden.
Under nogle af sine skråplanseksperimenter benyttede Galilei et pendul til tidsmåling, og man fandt i hans efterladte papirer en tegning af et komplet pendulur.
9. Om begrebet energi
På Galileis tid var begrebet energi ikke afklaret. Men her til slut skal vi beskrive et resultat af Galilei, som faktisk med moderne terminologi viser, at han var klar over, at når et legeme mister potentiel energi (beliggenhedsenergi), så vinder legemet det samme i kinetisk energi (bevægelsesenergi). I resten af dette afsnit ser vi bort fra andre påvirkninger end tyngden og påvirkningerne fra skråplanet. Først noterer Galilei en interessant sammenhæng mellem det frie fald og bevægelsen på et skråplan:
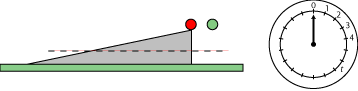 |
Vi kigger på et skråplan og starter samtidig to kuglers bevægelser: Den røde ruller ned ad skråplanet, den grønne falder frit. De starter i samme højde og med begyndelseshastighed 0. |
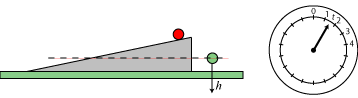 |
t sekunder senere er den grønne kugle kommet ned til den punkterede linie. Vi kalder den hastighed, den har på det tidspunkt, for h. På det tidspunkt er den røde kugle ikke kommet ret langt. |
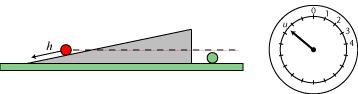 |
Så venter vi et godt stykke tid, mens den røde kugle ruller. Når der er gået u sekunder, er den røde kugle nået ned til den punkterede linie. Og så er Galileis resultat, at til tidspunktet u har den røde kugle samme hastighed h, som den grønne kugle havde kl. t. |
Det er let at bevise resultatet ved hjælp af hastighedsformlen (jfr. ovenfor)
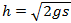
For letheds skyld tænker vi os, at skråplanet er 5 gange så langt som dets lodrette højde. Så bliver det stykke, den røde kugle bevæger sig frem til kl. u, 5 gange så langt som det stykke den grønne kugle bevæger sig frem til kl. t. Men hvis den grønne kugles acceleration er g, så er den røde kugles acceleration kun en femtedel af g; derfor får de to kugler samme hastighed, når de passerer den punkterede linie.
Resultatet kan også formuleres på en anden måde:

Hvis de tre kugler på figuren starter samtidig, så kommer de ikke lige hurtigt ned, men når de kommer ned, løber de lige hurtigt!
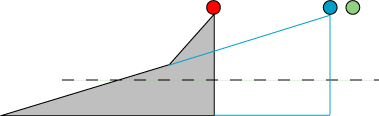
Mærkeligt nok forbliver resultatet rigtigt, også hvis skråplanet har en knæk på midten. For at indse det, tænker vi os et ekstra blåt skråplan, såden som det er vist på figuren. Vi tegner også en vandret punkteret linie, der ligger lavere end knækket. Så ved vi, at den blå og den grønne kugle har samme hastighed i det øjeblik, de passerer den punkterede linie. Vi starter nu den blå kugle så meget tidligere end den røde, at de kommer samtidig til knækket. Da de på det tidspunkt har samme højde, har de også samme hastighed. Derfor følges de ad efter knækket, og derfor har de samme hastighed som den grønne kugle ved passagen af den punkterede linie.
Tilsvarende resultater gælder også, hvis kuglerne starter for neden og på grund af opadrettede begyndelseshastigheder bevæger
sig op ad skråplanet og lodret op.
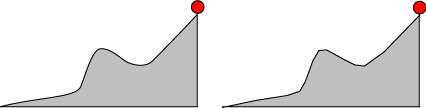
Til sidst kigger vi på et skrå"plan", hvis overflade er kurvet på en vilkårlig måde, f.eks. sådan som
det er vist på figuren til venstre. Sådan et skråplan kan tilnærmes, lige så godt man vil, med et skråplan,
der ikke er krumt, men i stedet har en masse knæk. Derfor må sætningen gælde, ligemeget hvilken kurve kuglen tvinges til at følge på
sin vej ned:
Hvis et legeme starter med hastighed 0 og under en vilkårlig bevægelse mister stykket s i højden da har det
sluthastigheden
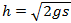 |
Den tilnærmelse til en krum kurve med en kurve bestående af liniestykker, som Galilei her foretager, er en forløber for integration.
I dag ville vi sige, at da den mistede potentielle energi er bestemt af faldet i højde, så kan den opnåede kinetiske energi også kun afhænge af faldet i højde.
Til slut skal vi gøre opmærksom på, at vi her har beskrevet Galileis resultater i et nogenlunde moderne sprog. På Galileis tid var
formelsproget ikke opfundet, og Galilei måtte derfor benytte det geometrisk prægede sprog, som oldtidens grækere havde udviklet.
På Galileis tid kendte man heller ikke koordinatsystemet, og begrebet vektor var ikke opfundet. Disse forhold gjorde det naturligvis
meget vanskeligere for Galilei både at finde og at fremstille resultaterne.
| Hvis du støder på et ord, hvis betydning du ikke kender, så søg på ordet. |