Forside Søgning Liste

1. Grænseværdi for talfølge

Vi kigger først på denne følge af tal:

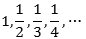
Meningen er, at der står uendelig mange tal, og de står vel at mærke i en bestemt rækkefølge. Tallene kaldes elementer i talfølgen. Det første element er 1, det andet er ½, og sådan fortsætter det. Hvis vi betegner det n-te element a_n , kan talfølgen kort beskrives, ved at man skriver

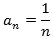
Det, vi skal beskæftige os med her, er, om a_n nærmer sig ubegrænset til et bestemt tal, når n vokser ud over alle grænser. I vores tilfælde er det klart, at a_n nærmer sig ubegrænset til 0, når n vokser ud over alle grænser. Man siger derfor, at talfølgen a_n har grænseværdien 0 for n→∞, og man skriver

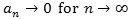
Vi går nu over til en vilkårlig talfølge a1, a2, a3, ... a_n, ...

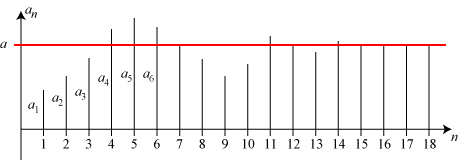
På figuren har vi afsat elementerne som lodrette liniestykker ud fra den vandrette akse. Desuden er der tegnet en vandret rød linie oppe i afstanden a over den vandrette akse. Den røde linie har en vis tykkelse, og den matematiske afstand a er op til midt i linien. Definitionen af, at talfølgen har tallet a som grænseværdi, lyder nu således: Lige meget hvor tynd den røde linie er tegnet, skal alle de lodrette liniestykker fra et vist nr. (her nr. 15) at regne ende inde i den røde linie. Når a_n har grænseværdi a, skriver vi a_n→a for n→∞ eller

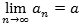
af latin "limes", grænse. Det er klart, at den talfølge, vi først betragtede, har grænseværdi 0 ifølge definitionen. For hvis liniens tykkelse f.eks. er en hundrededel (af den benyttede længdeenhed), vil endepunkterne fra og med nr. 201 ligge inde i liniens tykkelse. Der er mange talfølger, der ikke har nogen grænseværdi, f.eks. 1,-1,1,-1,1,-1, ... . En talfølge a_n som 1,2,3, ... , n, ... har ingen grænseværdi. Man siger i stedet, at a_n→∞ for n→∞. Man taler i alle tilfælde om en grænseovergang.

Vi tager et par eksempler til, hvor der er en grænseværdi:

Først betragter vi talfølgen

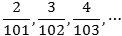hvor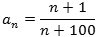

Man kan måske ikke lige se, hvad grænseværdien er, men hvis man forkorter brøken med n, går det bedre:

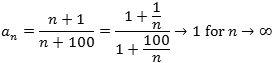
Grænseværdien er altså 1, da både 1/n og 100/n går mod 0 for n→∞.

Til sidst tager vi et eksempel, hvor resultatet ikke kan forudsiges:

Vi betragter talfølgen

,

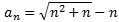altså

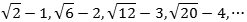
Man kan ikke finde grænseværdien bare ved at se på udtrykket for a_n . Begge led går mod uendelig for n→∞ og nogenlunde lige hurtigt, og så er det jo ikke godt at vide, hvad der sker med differensen. Men hvis man anvender en noget uventet omskrivning af udtrykket for a_n, går det:

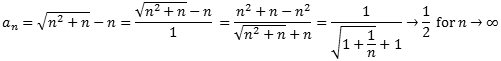
Eksemplet antyder, at begrebet grænseværdi kan give anledning til store vanskeligheder.

2. Uendelige summer

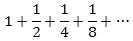
På forhånd har en sådan sum ingen mening. Man bliver jo aldrig færdig, når man skal lægge uendelig mange tal sammen. Man hvad nu, hvis man ville definere summen til at være et eller andet tal, hvad skulle det være for et tal? Hvis vi afsætter de første af tallene i forlængelse af hinanden på en tallinie, får vi følgende billede:

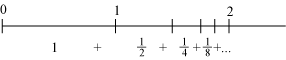
Først går man stykket 1, det er halvvejs hen til 2, og så er der 1 tilbage hen til 2.
Så går man videre stykket 1/2, det er halvvejs hen til 2, og så er der 1/2 tilbage hen til 2
Så går man videre stykket 1/4, det er halvvejs hen til 2, og så er der 1/4 tilbage hen til 2
Så går man videre stykket 1/8, det er halvvejs hen til 2, og så er der 1/8 tilbage hen til 2
Og sådan fortsætter det. Man kan altså aldrig komme over 2, når man lægger sammen forfra, men man kan komme lige så tæt på 2, som man vil. Derfor definerer vi nu summen af de uendelig mange tal til at være 2 og skriver

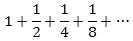=  2,

eller kortere

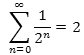
En sådan sum kaldes en uendelig række. At uendelig mange tal kan have endelig sum, er forklaringen på Zenons paradoks om Achilleus og skildpadden.

Vi går nu over til det generelle tilfælde og betragter rækken a1+ a2+ a3+ ... + a_n+ ... . For at definere rækkens sum lader vi s_n betegne summen af de n første led i rækken, s1= a1, s2= a1+ a2, s3= a1+ a2+a3, osv. s_n kaldes det n-te afsnit i rækken. Hvis så talfølgen s_n→s for n→∞, kalder vi rækken a1+ a2+ a3+ ... konvergent med sum s og skriver a1+ a2+ a3+ ... = s eller

.

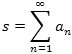Hvis talfølgen s_n ingen grænseværdi har, kaldes rækken a1+ a2+ a3+ ... + a_n+ ... divergent, og den tildeles ingen sum.

Som et vigtigt eksempel betragter vi den uendelige række

,

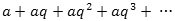hvor a ≠ 0 og q ≠ 0 er givne reelle tal, q ≠ 1. Rækken kaldes en uendelig kvotientrække. Når vi skal undersøge, om rækken er konvergent, skal vi kigge på det n-te afsnit

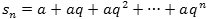
s_n kaldes en kvotientrække. Vi skal undersøge, om s_n har en grænseværdi for n→∞. For at finde ud af det er vi nødt til at finde en formel for s_n - uden 3 prikker i. Det kan man snedigt nok gøre sådan: Ved at multiplicere med q får man, at

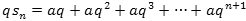
Ved subtraktion får man så, at

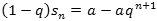
- og der røg de tre prikker. Der gælder altså følgende formel for kvotientrækken s_n :

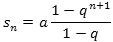
Den uendelige kvotientrække er altså konvergent med summen

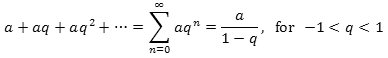
Det eksempel, som vi startede med, fremkommer af denne formel, ved at man sætter a = 1 og q = ½.

Til sidst giver vi et eksempel, der antyder, at teorien om uendelige rækker er meget indholdsrig:

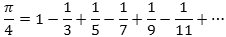
3. Grænseværdi for funktioner

Ligesom talfølger kan have grænseværdier, kan funktioner også have det. De præcise definitioner minder om dem for talfølger, og her nøjes vi med at illustrere det med nogle eksempler.

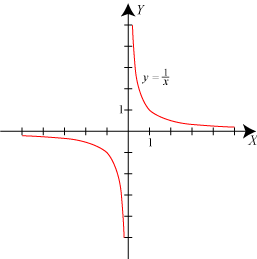Vi starter med funktionen y = 1/x, hvis graf er vist på figuren. Denne funktion har følgende 4 grænseværdiegenskaber: y → 0  for  x → ∞ y → ∞  for  x → 0  fra højre y → -∞  for  x → 0  fra venstre y → 0  for  x → -∞ Herudover kan man lade x gå mod et hvilket som helst tal, men det er ikke særlig interessant. F.eks. vil y → ½ for x → 2, men det kan man jo umiddelbart se på kurven.

Der er imidlertid en situation, hvor en funktion y = f(x) ikke er defineret for en bestemt værdi af x, lad os sige x = x₀, og hvor man er nået frem til funktionen med henblik på at bestemme dens grænseværdi for x→x₀. Vi tager et eksempel af denne type:

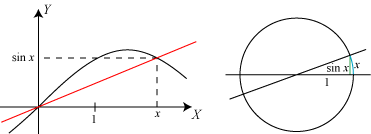
Lad os sige, at vi er interesseret i at bestemme hældningskoefficienten α for sinusfunktionens tangent i punktet (0,0). Vi vælger et x og tegner linien gennem (0,0) og (x, sin x). Denne linie har hældningskoefficienten

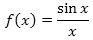
og α er så grænseværdi for f(x) for x→0. På figuren ovenfor til højre er der valgt en lille værdi af x, sin x er det lille grønne liniestykke, og x selv er den lille blå cirkelbue. Når x nærmer sig 0, nærmer længderne af de farvede stykker sig begge til 0, men samtidig nærmer de sig til at blive lige store, og selv om det ikke er et helt tilfredsstillende bevis, så overbeviser det os nok om, at

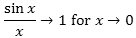
Den søgte hældningskoefficient er derfor α = 1.

Hvis du støder på et ord, hvis betydning du ikke kender, så søg på ordet.