DEFINITION AF HASTIGHED OG ACCELERATION

Definition af hastighed og acceleration

Helt tilbage i begyndelsen af 1300-tallet arbejdedes der med begreberne hastighed og acceleration. Mertonskolen og William Heytesbury definerede konstant hastighed og konstant acceleration med acceptabel præcision, men de nåede ikke frem til en definition af hastighed og acceleration til et bestemt tidspunkt for en vilkårlig bevægelse af en partikel. Stort længere kom man ikke før 1600-tallet. Galilei definerede hastigheden af en partikel til et bestemt tidspunkt som den konstante hastighed, som partiklen ville få, hvis man fra det pågældende tidspunkt fjernede alle ydre påvirkninger. Denne definition giver samme resultat som den, vi bruger i dag. Definitionen kunne også ved omhyggeligt planlagte forsøg benyttes ved målinger, men jeg har svært ved at se, hvordan den kan bruges ved teoretiske overvejelser.

Muligheden for at formulere præcise definitioner af begreberne hastighed og acceleration hænger nøje sammen med udviklingen af differentialregningen. De to begrebsdannelser blev udviklet under gensidig påvirkning, men her tænker vi os nu, at vi har differentialregningen til rådighed. Vi betragter først:

1. Bevægelse af en partikel på en ret linie

Vi betragter en lille rød partikel, der bevæger sig på en X-akse med begyndelsespunkt O. Vi tænker os, at bevægelsen er beskrevet ved, at vi til ethvert tidspunkt t kender afstanden x(t) fra O til partiklen. x(t) er altså en funktion defineret i et eller andet tidsinterval. Når vi nu skal definere hastigheden af partiklen til tidspunktet t, kan vi passende starte med at komme i tvivl, om det overhovedet giver mening at tale om hastigheden til et bestemt tidspunkt. En skeptiker kan jo indvende, at partiklen ikke kan nå at flytte sig til et bestemt tidspunkt. Det, der straks giver mening, er at tale om gennemsnitshastigheden i tidsintervallet fra t til t + Δt:

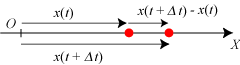
I dette tidsinterval har partiklen flyttet sig stykket x(t + Δt)- x(t), så den søgte gennemsnitshastighed bliver vejlængden divideret med tiden, altså differenskvotienten

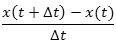
Her vil vores skeptiker sige noget i retning af: "Det kommer du ingen vegne med, for hvis du vælger et enormt lille Δt, vil tælleren blive enormt lille, og så får du det nul, jeg sagde ovenfor." Her tager vores skeptiker fejl. Både tæller og nævner bliver jo små, så man kan ikke på forhånd gætte, hvad der sker, når Δt→0. Men vi, der kender differentialregning, ved, hvad der sker:

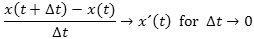
Vi definerer derfor partiklens hastighed v(t) til tidspunktet t ved at sætte v(t) = x´(t). I praktisk sammenhæng kunne man godt klare sig med at definere hastigheden ved differenskvotienten, men hvis man vil lave teori, er differentialkvotienten en bedre definition. Hastighedens dimension bliver LT⁻¹, den måles altså f.eks. i cm/sek eller km/time. Hastigheden er positiv, når partiklen bevæger sig i X-aksens positive retning, ellers er den negativ.

Vi går nu over til at definere begrebet acceleration. Acceleration er hastighedstilvækst pr. tidsenhed. Med samme betegnelser som ovenfor er gennemsnitsaccelerationen derfor

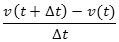
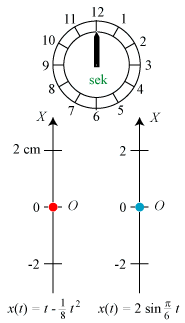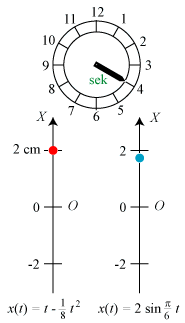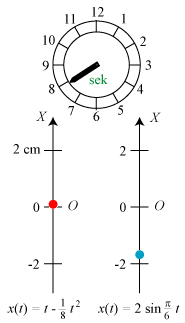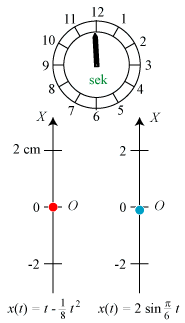og med samme begrundelse som ovenfor definerer vi derfor accelerationen w(t) til tidspunktet t ved at sætte w(t) = v´(t) = x´´(t). Accelerationen får dimensionen LT⁻². Vi illustrerer begreberne med animationen nedenfor.

Først den røde partikel, hvis afstand til O er x(t) = t-t²/8, t≥0. Partiklens hastighed bliver v(t) = x´(t) = 1 - t/4 cm/sek. Læg mærke til, at v(4) = 0. Det passer med, at for t = 4 sek, er den røde partikel højest oppe, og der skifter hastigheden fra at være positiv til at være negativ. Accelerationen for den røde partikel er w(t) = v´(t) = - ¼ cm/sek². Accelerationen er negativ, fordi hastigheden, der regnes positiv opad, er aftagende hele tiden. Accelerationen er altså konstant, men det kan man ikke umiddelbart se på bevægelsen. Bevægelsen minder imidlertid om den, man iagttager, når man kaster en rød bold lige op i luften, og i det tilfælde er der jo også konstant acceleration, nemlig tyngdeaccelerationen, der er ca. 1000 cm/sek².
Så går vi over til den blå partikel. Den bevæger sig sådan, at dens afstand fra O til tidspunktet t er x(t) = 2·sin (πt/6). En periode gennemløbes altså på 12 sekunder. Der er tale om en sinusformet svingning. Hastigheden til tidspunktet t er v(t) = x´(t) = π/3 ·cos(πt/6) cm/sek. Hastighedens største værdi er π/3 ≈ 1 cm/sek. Den opnås for t = 0 og - med modsat fortegn - for t = 6. Det ser rimeligt ud på figuren. Hastigheden er 0 for t = 3 og for t = 9, dvs. når partiklen er i en yderstilling. Den blå partikels acceleration bliver w(t) = v´(t) = -π²/18·sin(πt/6) cm/sek². Denne gang er accelerationen altså ikke konstant, den er 0 for t = 0 og for t = 6, altså når hastigheden er størst. Accelerationens største værdi er π²/18 ≈ 1/2 cm/sek². Den antages for t = 9, altså i nederste yderstilling. Det ser rimeligt ud, at hastighedstilvæksten her er størst i positiv retning.

2. Bevægelse af en partikel i planen eller rummet

Når en partikel bevæger sig på en orienteret linie, kan hastighedens retning bestemmes af dens fortegn, plus, når bevægelsen går i orienteringens retning, og minus ellers. Ved bevægelser i planen eller i rummet kan bevægelsen gå i alle mulige retninger. Man definerer derfor hastigheden som en vektor, hvis længde angiver farten, og hvis retning angiver bevægelsens retning. Vi formulerer det nu mere omhyggeligt. Da vi vil arbejde med vektorer, har vi i første omgang ikke brug for noget koordinatsystem. Vi kan klare os med et punkt O, som vi afsætter vektorerne ud fra. Vi betragter et rødt punkt, der bevæger sig. Banekurven er den grønne kurve på figuren nedenfor. Bevægelsen beskrives ved, at vi for ethvert t kender stedvektoren r(t).

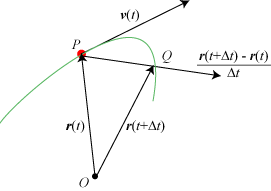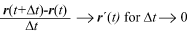Vi vil definere hastigheden af den røde partikel til et bestemt tidspunkt t, hvor partiklen befinder sig i punktet P. Vi venter nu et kort tidsrum Δt. I løbet af dette tidsrum har vores partikel bevæget sig fra P til Q, hvor OQ = r(t+Δt). Flytningen i tidsintervallet Δt er beskrevet af vektoren PQ = r(t+Δt) - r(t), og flytningen pr. tidsenhed bliver derfor

Det er på baggrund af denne grænseovergang naturligt at definere hastigheden af den røde partikel til tidspunktet t som v(t) = r´(t), altså som differentialkvotienten af vektorfunktionen r(t). Længden af hastighedsvektoren betegnes v(t); den kaldes partiklens fart. Hastighedsvektoren ligger hele tiden på banekurvens tangent.

På tilsvarende måde indser man, at det er naturligt at definere partiklens acceleration til tidspunktet t som vektoren w(t) = v´(t) = r´´(t), altså som grænseværdien

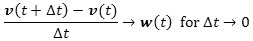
På figuren til højre vises konstruktionen af den vektordifferens, der står i tælleren. Til tidspunktet t er den røde partikel i P, og differensen er også afsat ud fra punktet P, som den bør være. Man ser, at accelerationen peger ind mod kurvens hulhed. Hvis farten er voksende, peger accelerationsvektoren fremad, og hvis farten er aftagende, peger accelerationsvektoren bagud. Hvis farten er konstant, bliver accelerationsvektoren vinkelret på kurven, dvs. på dens tangent. Med samme fart bliver accelerationsvektoren længere, jo mere kurven krummer.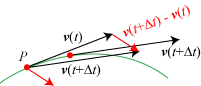

I definitionerne ovenfor har vi anvendt vektorer, men når man skal arbejde med konkrete eksempler, bruger man koordinater. I planen beskrives vektorfunktionen r(t) ved to koordinatfunktioner, r(t) = (x(t), y(t)), og i rummet er der tre koordinatfunktioner, r(t) = (x(t), y(t), z(t)). Hastigheder og accelerationer findes så ved koordinatvis differentiation. I planen vil f.eks. 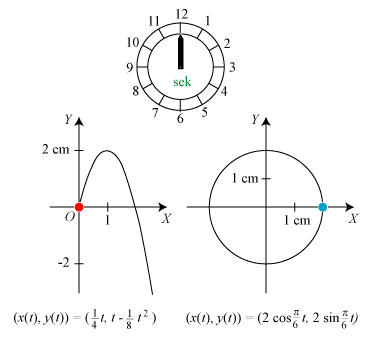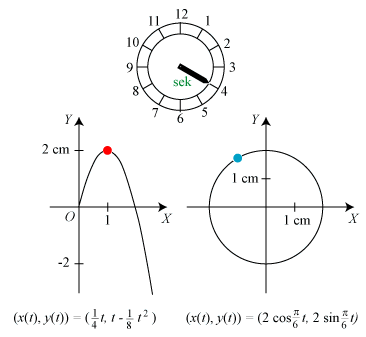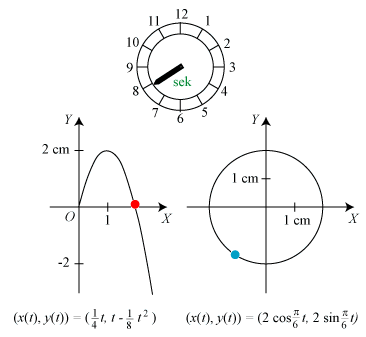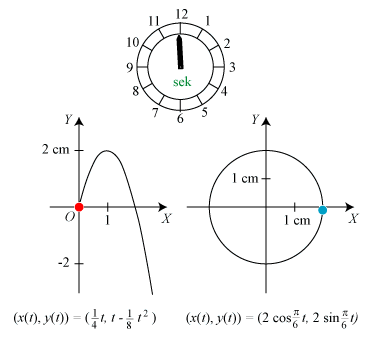hastighed og acceleration være v(t) = (x´(t), y´(t)) og w(t) = (x´´(t), y´´(t)). Animationen nedenfor illustrerer, hvordan det kan tage sig ud med plane bevægelser.

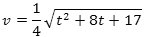Til tidspunktet t ≥ 0 har den røde partikel koordinaterne (x(t), y(t)) = (¼ ·t, t − 1/8 ·t²). Partiklen gennemløber derfor parabelbuen med ligningen y = -2x² + 4x, x≥0. Hastigheden til tidspunktet t er v = (¼, 1-¼ ·t). For t = 4 er hastigheden vandret, så på det tidspunkt er partiklen oppe i parablens toppunkt. Farten bliver

I startøjeblikket er farten altså ¼√17 = 1,031 cm/sek, mens den for t = 10 bliver = ¼√197 = 3,51 cm/sek.

Den røde partikels acceleration er w = (0,- ¼). Den er altså konstant og rettet lodret nedad. Det er ligesom tyngdeaccelerationen, så der er ikke noget at sige til, at det ligner en bold, der bliver kastet op i luften. Accelerationens størrelse er ¼ cm/sek². Farten vokser altså hvert sekund med ¼ cm/sek. På 10 sekunder bliver det 2,5 cm/sek, men 2,5 + 1,03 = 3,53, og det er jo ikke helt det samme som 3,51, hvordan det så ellers kan forklares?

Til tidspunktet t har den blå partikel koordinaterne (x(t), y(t)) = (2·cos πt/6, 2·sin πt/6). Partiklen gennemløber derfor cirklen med ligningen x² + y² = 4, og den er 12 sekunder om at gennemløbe cirklen én gang. Hastigheden til tidspunktet t er v = π/3(-sin πt/6, cos πt/6). Partiklens fart er derfor konstant, v = π/3 = 1,05 cm/sek. Det ser rimeligt ud på figuren.

Den blå partikels acceleration er w = - π²/18(cos πt/6, sin πt/6). Accelerationsvektoren er altså rettet ind mod cirklens centrum. Størrelsen af accelerationen er konstant, nemlig w = π²/18 = 0,55 cm/sek². Den konstante acceleration afspejler to ting: Dels, at farten er konstant, og dels, at cirklen krummer lige meget overalt. Læg mærke til, at w = v²/2. Det er et specielt tilfælde af en mere almen formel, som første gang blev fundet af Huygens i 1659.

Hvis du støder på et ord,
hvis betydning du ikke kender,
så søg på ordet.