Forside Søgning Liste

Hookes lov om fjederkræfter

Hookes egen beskrivelse af loven er kompliceret. Den handler om de deformationer, der opstår inde i et fast elastisk legeme, når det påvirkes af kræfter. Loven gælder kun, når påvirkningerne er svage, og kun for perfekt elastiske materialer som stål. Her vil vi kun betragte det tilfælde, hvor der er tale om en fjeder, der påvirkes af en udefra kommende kraft. Den beskrivelse, vi bruger, er moderne. Vi bruger differentialregning, der blev udviklet, kort tid efter at Hooke formulerede sin lov. På billedet til højre viser vi Hookes egen tegning, af hvordan han målte fjedres egenskaber. Den lodrette fjeder ABCD belastes med en vægt i vægtskålen forneden, og den tilsvarende øgning af fjederlængden kan aflæses på skalaen under vægtskålen. Den spiralformede fjeder foroven er i den ene ende fastgjort i midten af det mørke kors, som ikke kan bevæges. Den anden ende af fjederen er i punktet D fastgjort på en smal cylinder, der kan dreje sig om de 4 y-punkter. Vægtskålen hænger i en snor, der er viklet et stykke op om cylinderen. Snorens ene ende er fastgjort på cylinderen, og i den anden ende hænger vægtskålen. Når skålen belastes kan højden aflæses, og drejningsvinklen af cylinderen kan så beregnes. Denne slags fjedre bruges i ure med uro.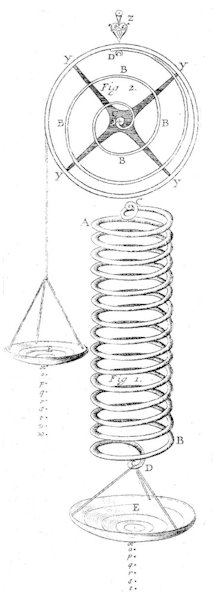

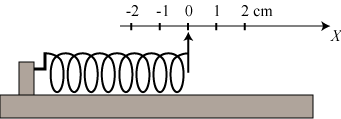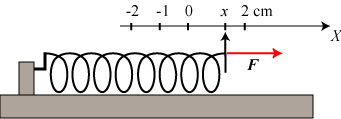
Til venstre viser vi en fjeder. Den er fastgjort i den ene ende, og i den anden ende er der en lille viser, der peger op på en inddelt skala. Hvis fjederen ikke er påvirket af nogen kraft, har den en bestemt længde. Den kaldes fjederens ligevægtslængde, og der, hvor viseren peger, skriver vi 0 på skalaen, som derefter inddeles i f.eks. cm. På figuren til højre påvirker vi fjederen med en kraft af størrelsen F, og det bevirker, at fjederen bliver længere. Viseren peger nu på et tal x på skalaen. Hookes lov siger nu følgende:

Fjederkraften F er proportional med fjederens forlængelse x, F = kx. Tallet k kaldes fjederkonstanten. Den måler, hvor stiv fjederen er.

Ligningen gælder med samme k, hvis kraften går den anden vej og bevirker en forkortelse af fjederen. Man regner både F og x med fortegn, i overensstemmelse med pilene på figuren. k kan f.eks. måles i newton pr. cm., N/cm.

Hookes lov har en helt anden karakter end f.eks. tyngdeloven. Det er jo klart, at hvis man trækker (eller trykker) tilstrækkeligt meget, så virker fjederen ikke længere. Man kan også finde materialer, der ikke opfører sig efter loven. På den anden side kan man lave fjedre, der med meget god tilnærmelse adlyder loven. Og det har så den fordel, at man kan regne på dem og sørge for, at de opfører sig, som man ønsker, når man indbygger dem i et maskineri. Fjedre bruges meget i praksis. Lige fra småbitte fjedre i mobiltelefoner til støddæmpere i biler.

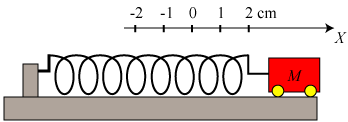
Lad os tage et eksempel på, hvad man kan opnå ved at bruge Hookes lov. Som vist nedenfor til venstre fastgør vi nu en letløbende vogn med masse M i fjederens højre ende, og vi trækker vognen 2 cm til højre og holder den fast der. Vi vil nu illustrere styrken af Hookes lov og Newtons 2. lov i forening ved at bruge lovene til at finde ud af, hvordan vognen vil bevæge sig, når vi giver slip på den til tidspunktet t = 0.

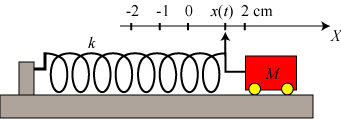Til højre viser vi situationen til et tidspunkt t. x(t) betegner altså positionen af højre ende af fjederen til tidspunktet t. Ifølge definitionen af acceleration er vognens acceleration w til tidspunktet t bestemt ved to differentiationer, w = x´´(t). Den kraft F, som fjederen påvirker vognen med, er modsat til den kraft, som vognen påvirker fjederen med, så F = -kx(t). Newtons 2. lov siger nu, at

Mx´´(t) = -kx(t)

I denne ligning er M og k kendte tal, og x(t) er en ukendt funktion. Ligningen kaldes en differentialligning, og ligninger af denne type spiller en stor rolle i fysikken. De er tit vanskelige at løse, men i vores tilfælde kan vi klare det. Vi bestemmer nu et positivt tal ω, så ω² = k/M. Så får differentialligningen formen

x´´(t) = -ω²x(t)

Det handler altså om at finde en funktion x(t), som differentieret to gange giver minus sig selv multipliceret med ω². I vores omtale af differentiation har vi nævnt, at x(t) så må have formen

x(t) = a·sin ωt + b·cos ωt

og nu kan man så se det fornuftige i at indføre dette ω. ω kaldes svingningens vinkelfrekvens; den måles i sek^-1. Hvis T er tiden for en hel svingning, er ωT = 2π.

Da vognen kører på en ganske bestemt måde, må det være muligt at bestemme a og b. Det gør man ved at benytte de såkaldte begyndelsesbetingelser. Begyndelsesbetingelserne er her, at x(0) = 2, og at x´(0) = 0, da vognen har fart 0 for t = 0. Den første betingelse medfører, at b = 2. Derfor er

x(t) = a·sin ωt + 2·cos ωt

For at kunne udnytte den anden betingelse må vi differentiere funktionen for at finde vognens hastighed:

x´(t) = aω·cos ωt − 2ω·sin ωt

Sætter vi her t = 0, får vi, at a = 0. Resultatet er altså, at vognens bevægelse er bestemt af formlen

x(t) = 2·cos ωt

Vognen svinger altså sinusformet frem og tilbage med amplituden 2 cm. Vi vil nu gerne have en svingningstid på 12 sekunder, dvs. en vinkelfrekvens, der er ω = π/6. Vi vælger altså M og k sådan, at ω får denne værdi. For dette valg af ω viser vi bevægelsen på animationen nedenfor.

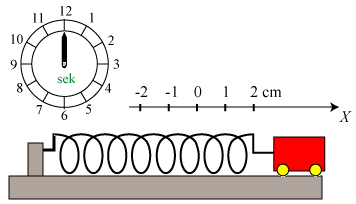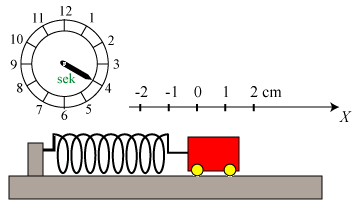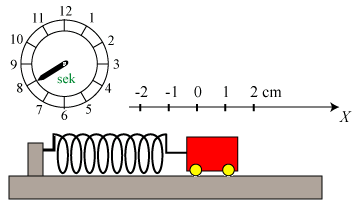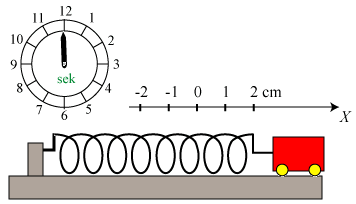
Vognens hastighed v (regnet med fortegn) til tidspunktet t fås ved differentiation. v = - π/3·sin ωt, hvor ω = π/6. Farten er altså størst, når fjederen har sin ligevægtslængde, hvilket man godt kunne have forudset.

Man kan få meget at vide af denne teoretiske behandling. Uanset begyndelsesbetingelserne bestemmes vognens svingning af ligningen

x(t) = a·sin ωt + b·cos ωt

Her angiver b den forlængelse, som fjederen har på starttidspunktet. Og af hastighedsformlen ovenfor følger, at starthastigheden er aω. Svingningstiden er T = 2π/ω. Svingningstiden er altså uafhængig af begyndelsesbetingelserne, og det kunne man ikke vide i forvejen. Uanset begyndelsesbetingelserne er svingningen sinusformet. Udtrykket for x(t) kan nemlig omskrives til en faseforskudt sinus, sådan som vi har nævnt det i omtalen af sinus.

Hvis du støder på et ord, hvis betydning du ikke kender, så søg på ordet.