HUYGENS´ ARBEJDER MED PENDULURET

Ind til listen:

Huygens arbejder med penduluret

1.Indledning

Efter at Columbus første gang rejste til Amerika, var lange sørejser blevet mere og mere almindelige. Det var derfor vigtigt at kunne bestemme breddegraden og længdegraden på et skib til havs. Breddegraden var let nok, den kan bestemmes på flere forskellige måder. F.eks. er (nord for ækvator) Polarstjernens højde over horisonten lig med stedets breddegrad. Men længdegraden er svær. Mange skibskatastrofer i perioden frem til ca. 1775 skyldtes, at man om bord på skibet havde bestemt længdegraden unøjagtigt.

Den bedste metode til længdebestemmelse til søs og mellem kontinenterne, som man kendte i 1600-tallet, var baseret på tidsmålinger. Metoden bygger på, at for hver gang man bevæger sig 15° vestpå, skal man trække en time fra lokaltiden. Lokaltiden forstået som den tid, hvor solen kulminerer kl. 12. Hvis man bevæger sig 15° østpå, skal man lægge en time til. Lad os sige, at vi har to ure, et, der går efter lokal tid, og et andet, der viser klokkeslættet i London. Hvis nu f. eks. londonuret viser, at klokken er 20 i London, mens den lokale tid er 18, må man være på 30 graders vestlig længde, altså ude i Atlanterhavet. Problemet var, at man på den tid ikke havde ure, der gik med den nødvendige nøjagtighed. Denne problemstilling inspirerede Huygens til livet igennem at forsøge at konstruere tilstrækkeligt nøjagtige ure. Før Huygens opfandt penduluret kunne selv de bedste ure have en fejl på 100 sekunder pr. døgn. Med sine pendulure kom Huygens ned på en fejl på 10 sekunder/døgn. Men selv det var ikke nok til længdebestemmelse på langfart tilsøs, - hvor pendulure for øvrigt ikke duede på grund af skibets bevægelser. Huygens konstruerede godt nok et pendulur med henblik på benyttelse til søs, men det kom ikke til at virke i praksis.

2. Om pendulers svingninger

Hvis man starter to ens meterlange penduler samtidig, det ene med 5 graders udsving og det andet med 10 graders udsving, så vil man se, at de svinger i takt. Det tager altså samme tid for et pendul at svinge 5 grader som at svinge 10 grader. Men hvis man ændrer de 10 grader til f.eks. 80 grader, kommer de hurtigt ud af takt. Det tager længere tid for et pendul at svinge 80 grader end 5 grader.

Når udsvingene er små, er svingningstiden for et pendul altså uafhængig af udsvingets størrelse. Det var, da man havde erkendt dette noget overraskende faktum, at man begyndte at lave pendulure. Her styrer et pendul, hvor hurtigt uret går. Tankegangen er følgende: Man kan ikke helt undgå, at udsvingene af et pendul i et ur i tidens løb ændrer sig en lille smule. Der kan komme lidt skidt i maskineriet. Den kæde, som et lod hænger i, bidrager mere til vægten, når loddet er langt nede, end når det er oppe. Og en fjeder, der er lige ved at løbe ud, trykker nok lidt mindre, end når den er stram. Sådanne fejlkilder kan man altså være ligeglad med, så længe udsvingene er små.

Det var Huygens´ fortjeneste, at han som den første underkastede pendulsvingningerne en teoretisk behandling. Han betragtede først det, som man i dag kalder matematiske penduler. Et matematisk pendul består af en partikel P med masse M, der er ophængt i en masseløs snor af længden l. Huygens fandt ud af, at når et sådant pendul udfører små svingninger i en plan, da er svingningstiden T bestemt af formlen

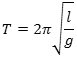
Huygens´ udledning af denne formel var lang og kompliceret. Vi giver her en udledning, der bygger på differentialregning. Da Huygens fandt formlen. var differentialregning ikke opfundet.

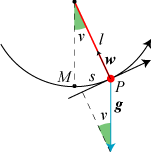På figuren kan det røde pendul svinge frem og tilbage på den sorte cirkelbue omkring ligevægtspunktet M. s = s(t) angiver længden af cirkelbuen fra M til P til tidspunktet t. s(t) er negativ, når P er til venstre for M. Opgaven er at finde ud af, hvad s(t) er for en funktion. Den grønne vinkel v = v(t) findes to steder på figuren. Den er også negativ, når P er til venstre for M.
I slutningen af "1670 Parameterfremstilling" har vi vist, at s´´(t) er den med fortegn regnede længde af projektionen på tangenten af accelerationsvektoren for P. Denne vektor kan skrives som en sum af to vektorer, nemlig tyngdeaccelerationen g og den acceleration w, der skyldes snorkraften. w er vinkelret på tangenten, og den bidrager derfor ikke til projektionen. Derfor er

s´´(t) = -gsinv,
hvor minuset skyldes, at længden af projektionen af g og v har modsatte fortegn.

Nu er vi så kommet til det sted i argumentationen, hvor vi antager, at udsvingene er så små, at vi kan sætte sinv = v. Da s = lv, får vi så, at s = s(t) kan bestemmes af differentialligningen

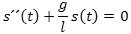
Til slut i "1670 differentiation" har vi nævnt, at s(t) så må have formen

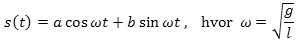
Her er a og b konstanter, der afhænger af, hvor og med hvilken fart pendulet er sat i gang. s varierer altså sinusformet med vinkelfrekvens ω. Det betyder, at svingningstiden er

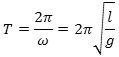
Hvis svingningstiden er 2 sek. kaldes pendulet et sekundpendul. Dets længde er

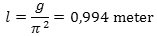
Hvis et sådant pendul bruges i et ur, siger uret et tik hvert sekund. Det er et tilfælde, at længden af et sekundpendul er så tæt på en meter.

3. Om Huygens´ urkonstruktioner

Huygens var først og fremmest matematiker. Det, han interesserede sig mest for i ure, var, hvordan man får et ur til at gå med stor præcision. Han fandt tre løsninger på dette problem:

Uret kan styres af et matematisk pendul med små udsving. Så er svingningstiden uafhængig af små ændringer i udsvingets størrelse. Som vi beskriver nedenfor kendte man på Huygens´tid kun en såkaldt spindelgang, når man skulle omsætte en pendulbevægelse til tandhjulene i et ur. Spindelgangen kræver desværre store udsving, ca. 90°, så det måtte man finde sig i på den tid.
Uret kan styres af et matematisk pendul, hvor pendulstangen er erstattet af en snor. Hvis snoren bevæger sig mellem cykloideformede skabeloner vil svingningstiden være uafhængig af udsvingets størrelse, også for store udsving. Læs nærmere om det under: "1656 Huygens". Dette er baggrunden for, at der benyttes cykloideformede skabeloner i det ur, som vi beskriver i næste afsnit.
Uret kan også styres af en uro. Uroen er først opfundet af Hooke ca.1658, men han publicerede det ikke. Uvidende om Hookes opfindelse genopfandt Huygens uroen i 1675. Opfindelsen var nærmest fremtvunget af vanskeligheden ved at holde et pendulur i konstant gang om bord på et rullende skib. Læs mere om uroen under: "1658 Hooke".

Omsætningen af en regelmæssig svingende bevægelse til en rotation af viserne i et ur frembød interessante tekniske vanskeligheder. Du kan læse om det under: "1656 Urets udvikling".

Huygens tog livet igennem initiativ til konstruktion af en lang række ure, hvoraf flere satte verdensrekord i nøjagtighed. Under denne virksomhed arbejdede Huygens tæt sammen med en række dygtige urmagere. Det var urmageren Salomon Coster fra Haag, som lavede de første pendulure i 1657, og som, efter aftale med Huygens, udtog patent på penduluret. Et af Costers ure fra 1657 findes endnu. Det kan ses på Boerhaave Museum i Leiden (Leyden) i Holland.

4. Beskrivelse af et af Huygens ure

4.1. Urværket

På figur A viser vi et af Huygens´ ure. Det er plate 28 fra Huygens´ bog Horologium Oscillatorium fra 1673, med mine tilføjelser med rødt. Figur A indeholder 4 figurer, der har navnene Fig.I., Fig.II., Fig.III. og Fig.IV. Fig.I. viser uret, og på Fig.III. nederst til højre er der billede af uret set forfra i en anden målestok og med pendulet tegnet anderledes. Urets gang styres af et sekundpendul. Det er knap en meter langt, og dets bevægelse fra den ene side til den anden tager 1 sekund.

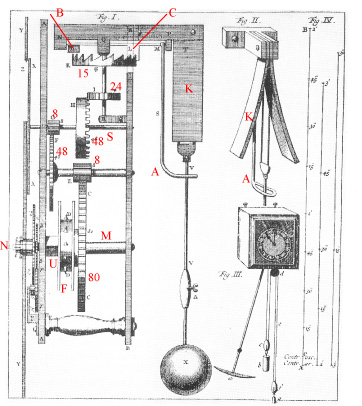Figur A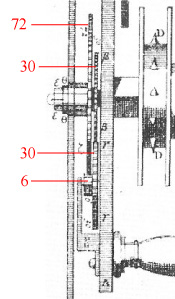

Figur B
Uret ses på figur A. Urets gang vedligeholdes af en vægt; den er ikke med på figuren. Vægten sørger for at det store 80-tandstandhjul drejer sig. Det skal ende med at dreje sig en gang rundt i timen. Den aksel, det sidder på, hedder minutakslen. Urets store viser sidder på venstre ende af minutakslen. Som vi senere skal se, kommer bevægelsen fra hjulet F på figur A.
80-tandstandhjulet sidder fast på minutakslen, og gennem 8, 48 og 8-tandshjulene drives sekundakslen S rundt én gang i minuttet. Sekundviseren sidder på S. Foroven ser man et mærkeligt formet tandhjul. Det ligner en dronningekrone, så det kaldes kronhjulet.

Fra S drives kronhjulet dobbelt så hurtigt rundt, altså en omgang på 30 sekunder, dvs. en tand på 2 sekunder. Omløbsretningen skal være sådan, at forreste del af kronhjulet drejer mod højre, og det passer med, at viserne går den rigtige vej rundt.
Så mangler vi kun at redegøre for den lille viser. Mekanismen vises på figur B. Den drives af det øverste 30-tandshjul, der sidder på minutakslen. Drejningen går videre til det nederste 30-tandshjul, der sidder på samme aksel som 6-tandshjulet. Det driver 72-tandshjulet, der altså drejer 12 gange så langsomt som minutviseren, passende til den lille viser. 72-tandshjulet sidder på en kort, tyk, hul aksel, der omslutter minutakslen. - På tegningerne kunne det se ud til, at viserne er erstattet af skiver, som fastsiddende pile peger på, men på fig.III på figur A kan man se viserne.

4.2. Hemværket

Her kommer vi til de to egentlige vanskeligheder ved at lave et nøjagtigt ur. Først skal man have et eller andet, der bevæger sig med en periode på et sekund. Og dernæst skal man have et såkaldt hemværk, der omsætter denne bevægelse til rotationen af tandhjulene i et ur.

Det første har vi beskrevet ovenfor. Det er et sekundpendul, der som nævnt er knap en meter langt. Hemværket er mere kompliceret. Huygens benyttede et "vergehemværk", også kaldet en "spindelgang". Det havde været kendt allerede i 13-hundredetallet og det blev i forbedrede udgaver brugt frem til midten af 18-hundredetallet. Her beskriver vi spindelgangen:

Øverst oppe på figur A er der lige over kronhjulet en vandret hvid aksel. På den sidder der en hvid flap C , der peger lodret nedad. Og længere til venstre på den hvide aksel sidder der en mørk flap B, der peger skråt ud mod iagttageren. Pendulets bevægelse forplanter sig via armen A til en rotation frem og tilbage af hvide aksel. Så flapperne drejer sig ca 90° frem og tilbage og en svingning frem og tilbage tager 2 sekunder.

Vi tænker os at pendulet er sat fast på den hvide aksel på en sådan måde, at når pendulet hænger lodret nedad, da peger den hvide flap skråt fremad, og den mørke flap peger skråt bagud. Flapperne skal være så lange, at kronhjulet i denne stilling ikke kan passere dem, og de skal være så lange, at de næsten kan nå ned i bunden af et tandmellemrum. Vi kender ikke deres præcise længde.

På billedet nedenfor beskriver vi, hvordan kronhjulets bevægelse dannes. Vi tænker os at tænderne er nummererede fra 1 til 15. Af praktiske grunde har vi kun tegnet dels de tre tænder, der ligger under den hvide flap samt de tre tænder, der ligger under den sorte flap, altså længst væk fra iagttageren. Den grå ellipse angiver hvor resten af kronhjulet er, og pilene angiver rotationsretningen. I højre søjle ses pendulet. Her ses den hvide aksel fra dens højre ende. Man skal altså her tænke sig, at den hvide flap er nærmere iagttageren end den sorte. Vi viser 5 øjebliksbilleder med ½ sekunds mellemrum.

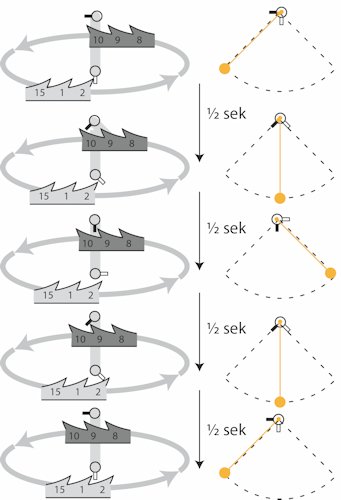Flapperne står stille i dette øjeblik, men drejer derefter mod uret. Den hvide flap ankommer fra højre og skubber på grund af pendulets tyngde kronhjulet en smule i den gale retning. Den hvide flap drejer sig derefter mod højre, og urværket neden under skubber kronhjulet i pilenes retning sådan at tand 2´s spids skubber til den hvide flap. Derved vedligeholdes pendulets bevæglse.

Flapperne drejer stadig mod uret Idet øjeblik tand 2 kan smutte under den hvide flap drejer kronhjulet hurtigt videre indtil tand 9 støder på den sorte flap. Når sammenstødet sker, sker der to ting:

Flapperne skifter bevægelsesretning og drejer så med uret A: På grund af pendulets tyngde trykker de sorte flap kronehjulet en smule i den gale retning.
B: Flapperne skifter nu til at dreje med uret, og trykket fra tand 9 understøtter pendulets bevægelse

Flapperne drejer stadig med uret Idet øjeblik tand 9 kan smutte under den sorte flap drejer kronhjulet hurtigt videre indtil tand 1 støder på den hvide flap. Når sammenstødet sker, sker der to ting:

Flapperne står stille i dette øjeblik, men drejer derefter mod uret. A: På grund af pendulets tyngde trykker de hvide flap kronehjulet en smule i den gale retning.
B: Flapperne skifter nu til at dreje med uret, og trykket fra tand 1 understøtter pendulets bevægelse.

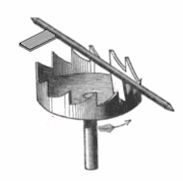
Der er altså hvert sekund en kort periode, hvor kronhjulet drejer den forkerte vej. Det er ikke en fejl, der summeres, så den påvirker ikke urets nøjagtighed. Men denne uregelmæssige bevægelse bevirker øget slid på flapperne, på kronhjulet og i lejerne. Denne fejl kan vist ikke undgås med spindelgangen, men der er i årenes løb gjort meget for at formindske den. Jeg ved ikke om Huygens kendte til dette arbejde.

På figur A, øverst til højre kan man se, at den øverste del af pendulophænget er to snore, der bevæger sig mellem skabelonerne K. Disse skabeloner bevirker ved store udsving en afkortning af pendullængden. De bevirker derfor, at svingningerne selv ved store udsving bliver ret ligetidige. I sine første ure formede Huygens skabelonerne på baggrund af eksperimenter. Senere lavede han en vidunderlig teori om deres form. Læs om det under: "1656 Huygens". Når vi her skriver"vidunderlig", er det teorien, vi beundrer. I praksis viste det sig, at det ikke virkede efter hensigten, så det har ikke været brugt.

4.3. Optrækket

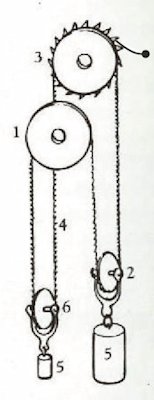Figur C
Under uret på figur A ser man de to lodder, som holder uret i gang, og som man bruger, når man skal trække uret op. Lodderne hænger i 4 snore På figur C her til venstre ser man, hvordan lodderne er hængt op. Det hjul, der på figur C hedder 1 hedder F på figur A. Det sidder fast forbundet med 80 tandshjulet, som drejer sig en omgang i timen, og som bærer urets minutviser. Det hjul, der hedder 3 på figur C er ikke vist på Fig. I. på figur A. Men jeg gætter på at det er den lille sorte cirkel, der sidder under uret på Fig. III. på figur A. - Det er ikke vigtigt, hvor det sidder. De 4 snore er altså i virkeligheden dele af en lukket kæde 4, der snor sig rundt om trisserne 1=F, 2, 3 og 6. På grund af spidserne i rillen på F kan kæden ikke glide på den trisse. Trisse 3 er kompliceret. Der er dels en rille, som den i F, og ved siden af rillen er der en række skrå tænder. Lige ved siden af trissen er der til højre fastgjort en fjeder, der forhindrer trissen i et dreje med uret. Hvis man prøver at dreje trissen mod uret løfter tænderne fjederen, så den vej kan trissen godt dreje. Det er det store lod 5, der driver uret. Det hænger i akslen på trisse 2. Den har en rille som kæden går i. Til højre går snoren op i rillen i trissen 3, ned om trisse 6, op i rillen i trisse 1(=F) og ned til trisse 2 igen.
Pointen med denne lukkede kæde med to lodder er, at man kan trække uret op, uden at det bevirker en uregelmæssighed i urets gang. Optrækket foregår ved at man hiver nedad i det lille lod 5 på figur C. Hjul 1 sidder fast på 80-tands hjulet på figur A, som drejer sig meget langsomt, en omgang i timen. Derfor bevirker optrækket ingen bevægelse af kæden fra det lille lod og op til hjul 1. Det der sker når man hiver nedad i det lille lod er derfor at hjul 3 drejer mod uret, så det store lod hæves.

Og hvad er så ideen? Jo, Det store lod 5 hiver hele tiden nedad i trisse 1 med halvdelen af sin vægt, både under optrækket og under normal gang. Trisse 1 sidder fast på 80-tands tandhjulet, og derfra går trykket videre opad i tandhjulskæden, helt op til kronhjulet. Trykket virker sådan, at den forreste del af kronehjulet presses mod højre. Trykkets styrke bestemmes af det store lod 5.

4.4. Afslutning

Senere arbejdede Huygens sammen med en meget dygtig parisisk urmager, Isaac Thuret, som også arbejdede sammen med Ole Rømer. Et af hans ure findes på Kroppedal Museum uden for København.

I januar 1675 opfandt Huygens uroen men Hooke hævdede at han havde fundet på det først. Vi viser Huygens´ første skitse af en uro til højre. Billedet er taget fra Huygens´ artikel i "Journal des Scavants" den 25. februar 1675. Øverst ser man hjulet, der drejer sig frem og tilbage. Nedenunder ses fjederen, der vedligeholder svingningerne, forhåbentligt med konstant svingningstid. Den lodrette aksel fører bevægelsen videre til resten af urværket. Hemværket er ikke vist på figuren. Det skal virke på samme måde som i uret ovenfor. Uroen gav mulighed for at lave meget mindre ure end pendulure. En mere betydningsfuld fordel ved ure med uro er, at de ikke på samme måde som pendulure forstyrres af et skibs rulning i hårdt vejr.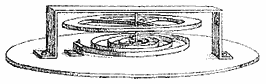

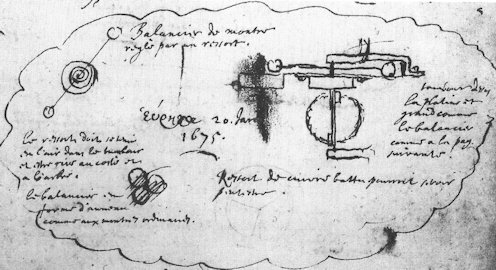
Vi slutter her med et stykke kladdepapir, som Huygens skrev den 20. januar 1675. Øverst til venstre er der billede af en uro, og dateringen står midt på billedet. Det er formodentlig den første beskrivelse af en uro!

Hvis du støder på et ord,
hvis betydning du ikke kender,
så søg på ordet.