|
Forside
Søgning
Liste |  |
Bestemmelse af accelerationen i en jævn cirkelbevægelse
I dag kan enhver, der kender lidt til differentialregning, bestemme
accelerationen i en jævn cirkelbevægelse. Sådan var det ikke i 1659, da Huygens som den første
bestemte denne acceleration. Det var der flere grunde til: Man havde ingen præcis definition
af begrebet acceleration. Begrebet en vektor var ikke klargjort, og regning med vektorer var ukendt.
Den metode, vi gennemgår her, er en noget moderniseret version af udregningen.
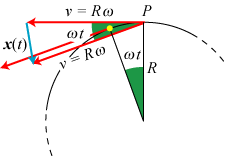
Vi tænker os, at en partikel bevæger sig rundt på cirklen mod uret med konstant fart v. Radius ud til partiklen drejer så med vinkelhastigheden ω = v/R. Partiklen er i cirklens øverste punkt P for t = 0, og til det tidspunkt vil vi finde accelerationen - der naturligvis har samme størrelse hele vejen rundt. Starthastigheden er den vandrette røde vektor. Vi vælger så et tidspunkt t lidt efter 0 og tegner den tilsvarende hastighedsvektor. Den udgår fra det gule punkt, hvor partiklen er til tidspunktet t. De to hastighedsvektorer er lige lange. Så parallelforskyder vi den anden hastighedsvektor, så den også får begyndelsespunkt i P. Den blå vektor x(t) vil da angive den ændring i hastigheden, der er sket i de forløbne t sekunder. Når t er lille, er x(t)/t så et fornuftigt bud på accelerationen, nemlig hastighedsændringen pr. tidsenhed. Vi vil nu bestemme accelerationens retning og størrelse hver for sig.
Først retningen: Da trekanten mellem P og den blå vektor er ligebenet, vil den blå vektor nærme sig til at blive lodret, når t nærmer sig 0. Accelerationen i punktet P er altså en vektor, der, når den afsættes ud fra P, peger ned mod cirklens centrum. Det var retningen.
Så kommer størrelsen: x(t) betyder længden af vektoren x(t). Størrelsen af accelerationen er størrelsen af hastighedstilvæksten pr. tidsenhed, når t er nær 0. Så vi skal finde ud af, hvad x(t)/t nærmer sig til, når t nærmer sig 0. Da de to grønne vinkler er lige store, nemlig ωt, gælder med meget god tilnærmelse, at x(t) = Rω·ωt. Derfor vil x(t)/t nærme sig Rω2.
Vi har altså vist, at størrelsen af accelerationen, når en partikel
bevæger sig med fart v på en cirkel med radius R, er
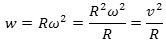
Læseren finder forhåbentlig argumentationen ovenfor en smule upræcis. Det er med velberåd hu at vi har formuleret det sådan. Huygens har nok haft lidt af den samme fornemmelse. Godt 10 år senere kom der mere orden i sagerne, og Newton genfandt da Huygens´ resultat med en mere solid matematisk underbygning.
Lad os nu sige, at partiklen har en vægt M, og at cirklen ligger i en vandret plan. Vi tænker os endvidere,
at partiklen holdes på plads i cirkelbanen af en snor, der igen holdes af en mand,
der står i cirklens centrum.
Huygens spørger så om, hvor meget han skal trække i snoren for at holde partiklen på plads i sin
cirkelbane. "Vis centrifuga", kalder han det,
"centrifugalkraften" F.
Huygens argumenterer så for, at F ligesom tyngdekraften er proportional med vægten M, og han siger
også, uden nærmere argumentation, at den er proportional med størrelsen w af accelerationen, så alt i alt gælder det, at
hvor k er en konstant, der kun afhænger af de valgte enheder for vægt, længde og tid. Huygens
foregriber her Newtons 2. lov i det specielle tilfælde, hvor der er tale om en jævn cirkelbevægelse.
| Hvis du støder på et ord, hvis betydning du ikke kender, så søg på ordet. |