| Ind til listen: |
Huygens´ princip og lysets brydning
1. Huygens´ princip
I slutningen af 1600-tallet blev der gjort mange forsøg på at forstå lysets natur. Forsøgene blev noget hæmmet af en teori om, at lyset er en bølgebevægelse i et medium, æteren, som består af små, hårde elastiske kugler, som ligger tæt op ad hinanden, og som findes i hele verdensrummet. Denne teori, som bl.a. blev udformet af Descartes, påvirkede også Huygens. Et af de problemer, som teorien rejste, var spørgsmålet om, hvor hurtigt lyset bevæger sig. Der var nogle, som troede, at lyset udbreder sig øjeblikkeligt, altså med uendelig stor hastighed. Huygens foreslog imidlertid et princip for lysets udbredelse, som vel kunne indpasses i æterteorien, men som på ingen måde kræver den. Derimod kræver Huygens´ princip, at lyset udbreder sig med endelig hastighed. Hvis du ikke ved ret meget om bølgebevægelser, er det nok en god ide at læse 1677 Bølgebevægelser, inden du fortsætter her.
I 1676 offentliggjorde Ole Rømer under sit ophold i Paris en artikel, hvor han påviser, at lyset har endelig hastighed. Da Huygens hørte om Rømers resultat, skrev han i et brev til Rømer den 11. november 1677, at Rømers resultat
| "... glæder mig så meget mere, fordi jeg, ved at antage, hvad du har bevist, nemlig at lysets udbredelse sker i tidens løb, uden uheld har forklaret alle lysfænomener, bl.a. den mærkelige brydning i islandsk krystal." |
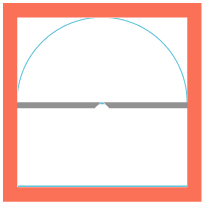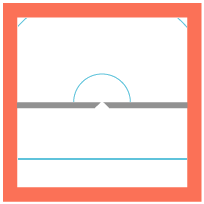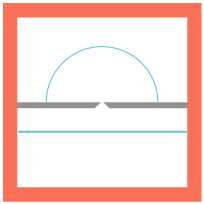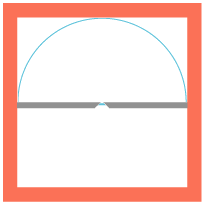
Huygens princip var inspireret af en iagttagelse, som illustreres nedenfor:
 |  |
|
|
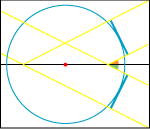
Inden vi kan formulere Huygens princip, må vi definere begrebet indhyllingskurve: Når man har en samling af uendelig mange blå kurver i en plan, findes der normalt en rød kurve med to egenskaber:
1. Den rører enhver af de blå kurver i et røringspunkt.
2. Den røde kurve indeholder ikke andre punkter end de nævnte røringspunkter.
Den røde kurve kaldes indhyllingskurve for
de blå kurver.
 |
På figuren er den røde kurve indhyllingskurve for et system af halvcirkler. I princippet er der uendelig mange halvcirkler, så hvert punkt af den røde kurve er røringspunkt med en halvcirkel. Jeg har naturligvis kun tegnet nogle af halvcirklerne. På tilsvarende måde kan man definere indhyllingsfladen for f.eks. et system af halvkugler. Et andet eksempel på en indhyllingskurve er nævnt under Torricelli (1644): En sikkerhedsparabel er indhyllingskurve for et system af kasteparabler. |
Vi kan nu formulere Huygens´ princip:
| Vi betragter en bølge på et bestemt tidspunkt. Bølgens bevægelse efter dette tidspunkt kan da bestemmes på følgende måde: Vi tænker os, at hvert punkt af bølgen er centrum for en halvcirkelformet (i rummet halvkugleformet) elementarbølge, der bevæger sig videre fremad. På et bestemt senere tidspunkt kan bølgens form da bestemmes som indhyllingskurven (i rummet indhyllingsfladen) for elementarbølgerne på dette tidspunkt. |
Huygens´ princip behandler én bølge ad gangen. Der er intet forsøg på at behandle samspillet (interferensen) mellem forskellige bølger i en bølgebevægelse. Huygens gør ikke noget forsøg på direkte at bevise princippet. Det retfærdiggøres af, at det giver fornuftige resultater. Det følger let af Huygens princip, at en plan bølgefront altid bevæger sig vinkelret på sin egen retning. På de sidste fire figurer nedenfor er de blå bølgefronter altså vinkelrette på de gule lysstråler. Tilsvarende bevæger et lille stykke af en krum bølgefront sig vinkelret på sin egen retning. Se nærmere om det under 1677 Soldaten og brydningsloven.
Her kommer to eksempler på, hvordan Huygens´ princip virker:
 | På animationen viser vi en retlinet bølge, der bevæger sig frem mod en dæmning, som der er en række små huller i. På den anden side af dæmningen starter elementarbølgerne, og man ser, hvordan deres forreste dele samarbejder mere og mere for til slut at danne indhyllingskurven, som er en ret linie, der fortsætter den bevægelse, som den oprindelige bølge havde. Hvis hullerne i dæmningen havde været tættere, ville linien være dannet hurtigere, og hvis der havde været huller over det hele, ville linien være dannet med det samme. Dette er et eksempel, hvor Huygens´ princip giver et korrekt resultat. Fysisk set er det kun korte stykker af elementarbølgerne, der bidrager til indhyllingskurven. |
Huygens´ princip ser bort fra de dele af elementarbølgerne, der ikke bidrager til indhyllingskurven. Huygens må have vidst, at det
ikke altid er korrekt. Lad os f.eks. kigge på animationen ovenfor. Vi tænker os nu, at den ændres, så der kun er huller i den
midterste tredjedel af dæmningen. Så vil man i et forsøg med vandbølger se, at der ud over en retlinet bølge over den midterste
tredjedel af dæmningen også
vil brede sig svage bølger ud til siden, hvilket elementarbølgerne også viser. Men hvis der specielt er tale om lysbølger, vil
disse svage bølger kun kunne iagttages, hvis
forsøget indrettes specielt med henblik på at få dem at se. Det hænger sammen med lysets korte bølgelængde, men det kunne Huygens
ikke vide noget om. Det skriver vi mere om (se under interferens).
| På figuren her viser vi, at man får korrekt resultat, hvis man anvender Huygens princip på en bølge, der udbreder sig cirkel- eller kugleformet fra et punkt. |  |
På forhånd skulle man tro, at hvis to bølgebevægelser i samme medium
krydser hinanden, så vil de påvirke hinanden. Ligesom det f.eks. vil resultere i kaos, hvis to marcherende regimenter af soldater
prøver at krydse hinanden. Huygens kendte imidlertid superpositionsprincippet for bølgebevægelser: Hvis to bølger i samme medium
møder hinanden, vil de krydse hinanden
uden gensidig påvirkning. Princippet er uhyre velkendt fra daglige iagttagelser: Hvis jeg kigger på en grøn skov, kan min kæreste
godt samtidig kigge på et rødt dannebrogsflag, også hvis de to synslinier krydser hinanden. Der sker ingen blanding af farverne.
2. Tilbagekastning
Vi går nu over til at undersøge, om bølgers tilbagekastning
fra et spejl eller en plan væg er en følge af Huygens´ princip. Så vi tænker os nu, at en plan bølgefront i et smalt
parallelbundt af lys bevæger
sig frem
mod et spejl. På figurerne tegner vi naturligvis kun det, der foregår i skærmens plan.
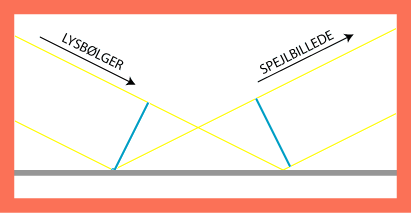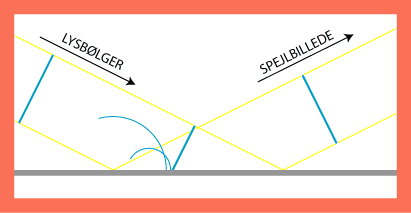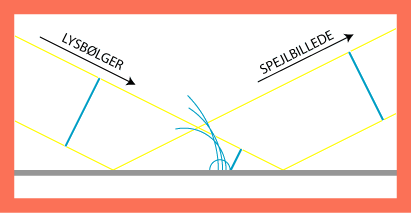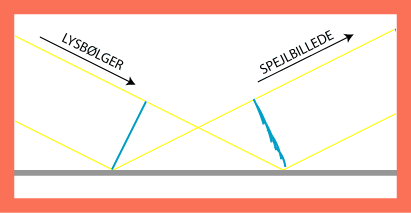
Så længe bølgefronten ikke er nået frem til spejlet, behøver vi ikke elementarbølger for at forudsige bevægelsen. Men når bølgen
når spejlet, er det ikke godt at vide, hvad der sker. Hver gang et punkt af fronten rammer spejlet, tænker vi os derfor, at der i punktet
starter en elementarbølge, der naturligvis kun findes på spejlets forside. Fem af disse uendelig mange elementarbølger er vist på
animationen, idet vi dog efterhånden udelader dele af elementarbølgerne, som ikke bidrager til indhyllingskurven. Som man ser
henne til højre, ender det tilsyneladende med, at elementarbølgerne bestemmer en retlinet (rettere plan) bølgefront, der bevæger sig
videre mod højre. Den tilbagekastede bølgefront er der faktisk hele tiden, efter at fronten er nået frem til spejlet. Et enkelt
sekund af dens bevægelse er vist på animationen. På animationen ser det ud, som om den tilbagekastede lysstråle danner samme vinkel med
spejlet som den indfaldende lysstråle. Og dette faktum følger faktisk, som vi nu skal se, af Huygens´ princip.
 |
På figuren viser vi foroven til højre den tilbagekastede blå bølgefront på et bestemt tidspunkt, og nedenunder viser vi, hvor den samme bølgefront ville være på samme tidspunkt, hvis spejlet ikke var der. Spejlet er tegnet som den vandrette sorte linie. Endvidere viser vi, hvor en tilfældig af de elementarbølger, som vi betragtede ovenfor, befinder sig på samme tidspunkt. Det er den blå cirkel. Den har centrum i det fremhævede røde punkt. Pointen er nu, at den øverste halvdel af den blå cirkel er elementarbølge for den tilbagekastede lysbølge, mens den nederste halvdel af cirklen er elementarbølge for den lysbølge, der ville være der, hvis spejlet var væk. Den blå cirkel berører derfor begge de blå bølgefronter. Det samme gælder for alle de andre elementarbølger, som vi betragtede ovenfor. Men da alle elementarbølgerne ligger symmetrisk om spejlet, må de to blå bølgefronter også ligge symmetrisk om spejlet. Heraf følger, at også den tilbagekastede bølgefront er retlinet (plan), og derfor må den orange vinkel være lig den grønne vinkel. Man kan også med noget besvær indse, at en enkelt lysstråle (dvs. et meget smalt strålebundt) tilbagekastes i den plan, der er bestemt af den indfaldende stråle og normalen til spejlet i det punkt, hvor strålen rammer spejlet. Tilbagekastningsloven er derfor en følge af Huygens´ princip. I 1657 havde Fermat fundet en anden model for bølgebevægelser, som også førte frem til tilbagekastningsloven. |
3. Brydning
|
Til slut går vi nu over til at se på, hvordan Huygens´ princip behandler lysets brydning. (Læs først om det hos 1621 Snell, ellers kan
du ikke værdsætte det, som sker nu.) Lysets brydning illustreres på animationen. Lyset kommer oppe i luften med lyshastigheden
c = 300.000 km/sek. Så rammer det en stærkt brydende glasklods, hvor lyshastigheden er | 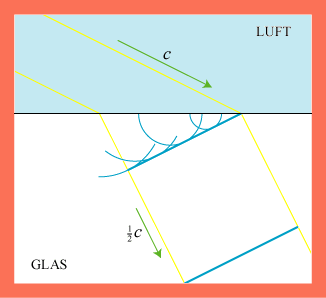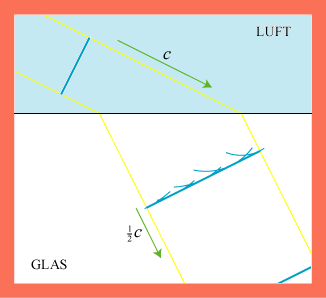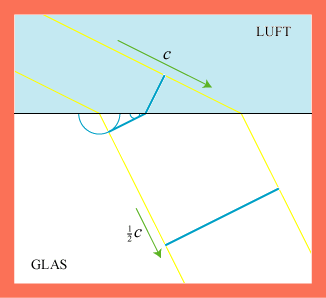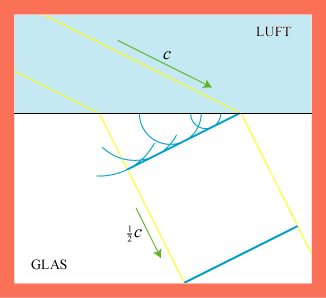 |
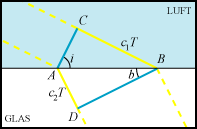 |
Vi går nu over til at vise, hvordan man med Huygens´ princip kan beregne den retningsændring, som lyset får, når det går fra f.eks. luft med lyshastighed c1 til f.eks. glas med lyshastighed c2 via en plan skilleflade. Figuren viser lysstrålen begrænset af de gule linier, og den viser en bestemt bølgefront til to forskellige tidspunkter: Øverst ses bølgefronten i det øjeblik, hvor det første punkt af fronten når frem til glasset. Og nedenunder ses fronten T sekunder senere, hvor dens sidste punkt forlader luften. På figuren er altså BC = c1T og AD = c2T. De to vinkler, der er vist på figuren, er indfaldsvinklen i og brydningsvinklen b. Af trekant ABC fås, at AB = c1T/sin i, og af trekant ABD fås, at AB = c2T/sin b. Af disse formler følger nu, at |
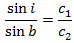 |
Formlen udtrykker, at Snells brydningsforhold er forholdet mellem de to lyshastigheder. Det er en fantastisk opdagelse! Formlen
kan bruges til bestemmelse af lyshastigheden i glas, hvis man kender lyshastigheden i luft. Man behøver jo blot at måle i
og b.
| Hvis du støder på et ord, hvis betydning du ikke kender, så søg på ordet. |