Forside Søgning Liste

1. Indledning

Huygens´ arbejde med stødet startede i 1652, og det fandt en foreløbig afslutning i 1656, da Huygens blev færdig med manuskriptet til bogen "De motu corporum ex percussione" (Om bevægelsen af legemer udsatte for stød). For fysikkens udvikling var det ærgerligt, at bogen først udkom i 1703, 8 år efter Huygens´ død. Huygens holdt imidlertid foredrag om emnet både i Paris og London i 1668. Gennem disse foredrag og gennem personlige møder og brevveksling nåede et vist kendskab til resultaterne alligevel rundt i den videnskabelige verden.

Som helt ung var Huygens betaget af Descartes´ opfattelse af den fysiske verden. Descartes opfattede den fysiske verden som sammensat af små partikler i evig bevægelse i forhold til hinanden. Og i et system uden vekselvirkning med resten af verden opfattede han bevægelsesmængden, dvs. summen af produkterne af masse og fart, som konstant. Med dette grundsynspunkt formulerede Descartes et aksiomssystem, som faktisk indeholdt selvmodsigelser og påstande, der ikke stemte med erfaringen. Huygens opdagede tidligt disse mangler i Descartes´ teori, og "De motu corporum ex percussione" kan ses som et vellykket forsøg på at give en mere korrekt fremstilling af det fuldstændig elastiske stød. For, som Huygens formulerede det: "Jo større myndighed den har, som fremstiller en vildfarelse, des nyttigere er det, at den gendrives".

Huygens fremstillede i sin bog teorien om det fuldstændig elastiske stød aksiomatisk. Det er et ideal, der stammer fra den klassiske græske geometri, og som bl.a. også blev benyttet af Archimedes. Huygens havde en speciel grund til at benytte en aksiomatisk fremstilling. Han gik nemlig ud fra aksiomer, som også tilhængere af Descartes måtte anse for korrekte. Og på grundlag af aksiomerne kunne Huygens så vise sætninger, der strider mod Descartes´ opfattelse. Vi giver eksempler nedenfor, og du kan læse mere om det under 1637 Descartes.

2. Aksiomerne

1. Gennem to forskellige punkter går der en kun én ret linie.

2. Når A og O er forskellige punkter i en plan, findes der i planen en cirkel, som har centrum i O og som går gennem A.

Det var Euclids store bedrift, at han kunne opbygge den kendte geometri på ret få aksiomer. Denne succes smittede af på fysikken. F.eks. opbyggede Archimedes sin teori om vægtstangen på et lille udvalg af aksiomer. Kriteriet på, at man har valgt nogle fornuftige aksiomer inden for fysikken, er dels, at aksiomerne virker umiddelbart indlysende, men mest, at det man kan bevise ved hjælp af aksiomerne stemmer med virkeligheden. Endnu i 1600-tallet brugte fysikere undertiden en aksiometisk fremstilling. Det gav nemlig en vis autoritet, at bruge de gamle grækeres metode. Senere indså fysikerne, at aksiomer rettelig høre hjemme i matematikken.

Huygens antog gyldigheden af følgende aksiomer:

1. Inertiloven: Et hvilket som helst legeme, en gang sat i bevægelse, fortsætter, hvis der ingen hindring er, sin bevægelse med stedse samme hastighed og efter en ret linie.
2. Relativitetsprincippet: Legemernes bevægelse og lige eller ulige store hastigheder er relative begreber, idet de skal henføres til andre legemer, der betragtes som hvilende, selv om måske både disse og de førnævnte legemer deltager i en anden fælles bevægelse. Og deraf følger for et sammenstød mellem to legemer, at selv om hvert af dem er underkastet endnu en anden jævn bevægelse, vil en iagttager, der følger med i denne fælles bevægelse, se, at de to legemer udøver nøjagtig den samme virkning på hinandens bevægelse, som hvis de alle havde været fri for denne bevægelse.
3. Vi antager, at når to ens legemer møder hinanden med samme hastighed, viger hvert af dem tilbage med samme hastighed, hvormed det kom.
4. Hvis et større legeme møder et mindre, som er i hvile, meddeler det dette nogen bevægelse, og mister følgelig noget af sin egen.
5. Hvis det ved et møde mellem to hårde legemer hænder, at det ene af dem efter stødet har bevaret hele den fart, som det havde, så vil heller ikke det andets fart være blevet større eller mindre.
6. Torricellis princip: To forbundne legemer kan ikke sætte sig i bevægelse medmindre deres fælles tyngdepunkt bevæger sig nedad.

Lad os kort kommentere nogle af aksiomerne: Inertiloven var tidligere formuleret af Galilei, dog med den forskel, at Galilei også opfattede en jævn cirkelbevægelse som en inertibevægelse, der kunne foregå uden ydre påvirkning. Descartes havde en korrekt formulering af inertiloven, men han udledte loven af Guds uforanderlighed. Huygens henviste mere ædrueligt til, "at den øjensynligt bekræftes af erfaringen".

Relativitetsprincippet fastslår, at når to iagttagere bevæger sig jævnt i forhold til hinanden, da har deres iagttagelser samme gyldighed. Her har Newton et andet synspunkt, idet han tror på eksistensen af en absolut bevægelse. I Principia skriver han i 1687 følgende: "Det absolutte rum, af natur uden relation til noget som helst udenfor, forbliver altid uforandret og ubevægeligt. Absolut bevægelse er en flytning fra det ene absolutte sted til det andet".

Ved stød mellem to legemer, der ikke er fuldstændig elastiske, vil aksiom 3 være forkert. Det gælder f.eks. ved sammenstød mellem to kugler af blødt ler eller af bly.

Torricellis princip blev formuleret i 1644. Torricelli forklarer selv, hvad han mener med "forbundne": Forbindelsen skal være sådan, at bevægelsen af det ene legeme bestemmer bevægelsen af det andet, f.eks. ved en vægtstang, en talje eller en hvilken som helst anden mekanisme.

Vi gennemgår i de følgende afsnit en række af de argumenter, hvormed Huygens udleder nye resultater af aksiomerne. Vi starter med

3. Stød mellem legemer med samme masse

Sætning 1: Når et legeme er i hvile, og et andet magen til rammer det, så vil efter stødet det andet være i hvile, og det første vil have den hastighed, som det andet havde før stødet

Om bord på båden på animationen er der to sømænd. De planlægger at illustrere aksiom 3 ved et forsøg om bord på deres skib, der sejler 5 km timen. De har medbragt to ens fuldstændig elastiske kugler. Den ene er rød og den anden blå. Til en start anbringer de den blå kugle i skibets forstavn, og den røde i agterstavnen. De aftaler så, at når der lyder et BUM! skal de støde lige kraftigt på hver sin kugle, så kuglerne bevæger sig ind mod skibets midte med en fart på 5 km/t. På animationen kan man se, hvad der sker: De to kugler støder sammen midt på skibet, og efter stødet bevæger de sig væk fra midten, stadig med en hastighed på 5 km/T. De ender samtidig i hver sin stavn af skibet. Sømændene kan konkludere, at bevægelsen stemmer med aksiom 3. Dæk for græsset på skærmen med et stykke papir, så kan du forstå sømændenes synspunkt.

Nu står der så inde på græsset en iagttager, der også lytter til sømændenes konklusion. Nej, siger han, det er slet ikke det, der foregår. Når BUM´et lyder, standser den blå kugle sin bevægelse, mens den røde kugle øger sin hastighed til 10 km/T. Efter lidt tid støder den røde kugle så ind i den stillestående blå kugle til højre. Ved stødet sker der så det, at den røde kugle standses, mens dens hastighed overtages af den blå kugle. Iagttageren på land ser altså, at det passer med sætning 1. Man kunne have erstattet hastighederne 5 og 10 km/t med hastigheder på v og 2v, og det er nu en følge af relativitetsprincippet, at begge parter har ret. Så vi har vist, at sætning 1 følger af aksiomerne 2 og 3.

Argumentet ovenfor kan sammenfattes i diagrammet til højre. Vi får brug for den slags diagrammer længere nede på siden, derfor forklarer vi her, hvad diagrammet viser. Først og fremmest er det vigtigt, at vi går over til at regne hastigheder med fortegn. En hastighed er positiv, hvis den er rettet mod højre, og negativ, hvis den er rettet mod venstre. Alle pilene på figuren peger mod højre. Bevægelsesretningen fremgår af fortegnet. F.eks. bevæger den første blå og den anden røde kugle i A-linien sig mod venstre. Linien mærket A viser, hvordan bevægelsen er set fra båden. Det vil typisk være en situation, hvor bevægelsen efter stødet kendes. Så kommer båden med farten angivet. Den fart kan vi selv bestemme, og det gælder så om at vælge en fart, som giver et interessant resultat nede i linie B. I linie B vises hastighederne set fra land. Der fremkommer alle hastighederne af dem i A ved addition af bådens hastighed. Og det følger så af relativitetsprincippet, at når påstanden i A er rigtig, da vil påstanden i B også være rigtig. Fordelen ved at regne med fortegn er, at man uanset bevægelsesretningerne i A skal addere bådens fart i alle fire tilfælde.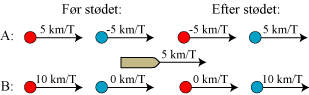

Huygens kunne ikke bruge en animation til støtte for sine argumenter, men han havde en anden, helt vidunderlig fremstilling. Billedet nedenfor er fra "De motu corporum ex percussione".

Man ser båden og to mænd, én i båden og én på land. De står med ansigtet mod hinanden og holder i hinandens hænder og holder to snore med ens kugler i. Billedet viser starttidspunktet. Manden i båden vil nu efterprøve aksiom 3. Han vil derfor først bevæge armene ind mod hinanden, hver med 5 km/T, så kuglerne støder sammen, og han vil bagefter med armene følge kuglernes bevægelser efter stødet. Manden på land vil hellere efterprøve sætning 1. Han vil derfor holde den højre arm udstrakt og bevæge den venstre arm mod højre med 10 km/T. Efter stødet følger også han med i kuglernes bevægelse. Man kunne nu være bange for et skænderi, men det er der ingen risiko for: De to mænd kan nemlig på grund af bådens bevægelse med 5 km/t mod højre begge gøre som planlagt, uden at slippe hinandens hænder. F.eks. starter manden i båden med at bevæge sin højre arm ind mod bådens midte med 5 km/t. Set fra land bevæger hans højre hånd sig 10 km/t. Så det passer med "landmandens" ønske. Jeg håber, at læseren kan se det for sig!

På animationen til højre vil de to sømænd endnu en gang efterprøve aksiom 3 ved forsøg. For at få et pænt resultat vælger vi to hastigheder, v > 0 og u < 0, og beder sømændene sejle båden med hastigheden h = ½(v+u), og når BUM!-et lyder starte de to kugler mod hinanden med hastigheden k = ½(v-u). Sømændene konstaterer igen, at de to kugler efter stødet bevæger sig væk fra hinanden med samme fart som før stødet. Hvordan ser iagttageren på land kuglernes bevægelse? Vi starter med den røde kugle. Set fra land bevæger den sig før stødet med hastigheden

h+k = ½(v-u) + ½(v+u) = v, og efter stødet har den set fra land hastigheden ½(u - v) + ½(v + u) = u

Så kommer den blå kugle: Set fra land bevæger den sig før stødet med hastigheden ½(u-v) + ½(v+u) = u, og efter stødet har den set fra land hastigheden ½(v-u) + ½(v+u) = v

Vi har dermed af aksiomerne udledt

Sætning 2: To ens legemer, der bevæger sig mod hinanden med to forskellige hastigheder, bytter hastigheder efter stødet.

På animationen bevæger den røde kugle sig tre gange så hurtigt som den blå før stødet, men efter stødet bevæger den blå kugle sig 3 gange så hurtigt som den røde.

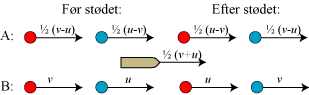
Det er faktisk lettere at følge argumentationen på diagrammet her. A - linien beskriver det velkendte stød mellem to ens legemer, der støder mod hinanden med samme hastighed. Vi ved så, at kuglerne efter stødet vil fjerne sig fra hinanden, begge med den samme hastighed, som de havde før stødet. I B - linien har vi fire gange adderet bådens hastighed og kan aflæse, at når kuglerne nærmer sig hinanden med hastighederne v og u, så bytter de hastighed inkl. fortegn ved stødet.

4. Stød mellem legemer med forskellig masse

Indtil nu har vi betragtet to ens, fuldstændig elastiske legemer. På resten af siden her betragter vi to forskellige, fuldstændig elastiske legemer. Vi starter med det tilfælde, hvor det ene legeme er i hvile inden stødet:

Sætning 3: Ved et stød mellem to forskellige legemer, hvor det ene er i hvile før stødet, bevares hastighedsdifferensen (på nær et fortegnsskift) efter stødet.

Denne gang viser vi ingen animation, vi argumenterer i tilknytning til diagrammer. På diagrammet til højre har den røde kugle i A-linien hastighed 0 før stødet, og den blå kugle har hastighed b. På diagrammet må b være negativ, for at vi kan få et stød. Efter stødet får den røde kugle en hastighed, som vi kalder -a. Vi vil nu prøve på at finde ud af, hvad der skal stå på spørgsmålstegnets plads. Det gør vi ved at give båden hastigheden ½ a. Dette valg retfærdiggøres af, at der kommer noget fornuftigt ud af det. I B-linien får vi så umiddelbart de tre første tal og kan til vores glæde konstatere, at den røde kugle beholder sin hastighed efter stødet, dog naturligvis med fortegnsskift. Så kan vi bruge aksiom 5 og slutte, at der skal stå -b-½ a på den sidste plads i B-linien.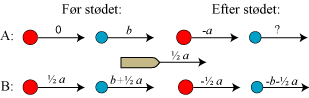

Nu kender vi sidste tal i B-linien og bådens hastighed. Så må sidste tal i A-linien være differensen (-b-½a)-½a = -b-a. Heraf fås nu, at hastighedsdifferensen efter stødet er (-b-a)-(-a) = -b. I linie A bevares hastighedsdifferensen altså på nær fortegn, og hermed er sætningen bevist.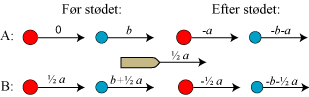

Nu kan vi så droppe forudsætningen om, at det ene legeme skal have begyndelseshastighed 0:

Sætning 4: Ved et stød mellem to forskellige legemer med begyndelseshastighederne c og d bevares hastighedsdifferensen (på nær et fortegnsskift) efter stødet.

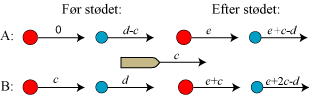I diagrammet vælger vi begyndelseshastighederne i A-linien til 0 og d-c. Efter stødet kalder vi den røde kugles hastighed for e. Ifølge sætning 3 er den blå kugles hastighed efter stødet da e+c-d. Så giver vi båden hastigheden c, og derefter kan vi aflæse sætning 4 i B-linien.

Også de følgende sætninger handler om stød mellem forskellige legemer. Vi viser først sætning 5. Men vi advarer: Beviset er vanskeligere end de foregående beviser.

Sætning 5: Når to legemer bevæger sig mod hinanden med hastigheder, der er omvendt proportionale med masserne, så får de efter stødet de samme hastigheder, dog med modsat fortegn.

Inden vi går i gang med selve beviset, får vi brug for et lille geometrisk hjælpesætning:

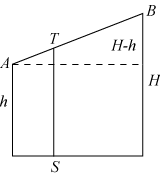Om figuren til venstre er det givet, at Da AB = AT + TB = TA·(k+1) vil

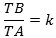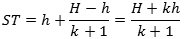Denne bestemmelse af ST får vi brug for i beviset for sætning 5, som kommer nu:

Det foregår helt anderledes end de foregående beviser: Vi betragter et blåt legeme med masse m og et rødt legeme med masse k·m. Det røde legeme giver vi en starthastighed v, og det blå legeme skal så have starthastigheden -kv.Vi tænker os, at det røde legemes starthastighed kommer i stand ved, at legemet falder stykket h1 = v2/2g fra punktet A. Legemet rammer så den lille skrå flade, og hastigheden bliver vandret af størrelse v ifølge Galilei. Tilsvarende giver vi det blå legeme sin starthastighed ved samtidig at lade det falde højden H1 = k2v2/2g fra punktet B. Det rammer så den lille skrå flade og får hastigheden -kv. Vi vil nu vise, at det røde legeme efter stødet får hastigheden -v. Beviset er indirekte, det vil sige, at vi antager, at det, vi skal vise, er forkert, og så vise, at denne antagelse fører til en modstrid. Vi antager altså, at den røde kugle efter stødet har hastigheden -v+c, hvor c ≠ 0. Da den relative hastighed er uforandret efter stødet, må den blå kugle efter stødet have hastighed c+kv.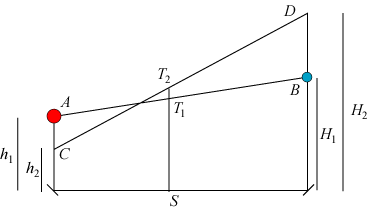

Efter stødet bevæger den røde kugle sig hen mod den lille skrå flade og bliver af den kastet op i luften med begyndelseshastighed -v+c. Den når så op i højden h₂ = (-v+c) ²/2g, og der fastholder vi den. Den blå kugle rammer sin lille skrå flade og bliver kastet opad med hastigheden c+kv. Den når derfor op i højden H₂ = (c+kv)²/2g, hvor vi fastholder den.

Nu har de to kugler af egen drift bevæget sig fra positionen AB til positionen CD, og vi vil nu kigge på, hvad der er sket med deres tyngdepunkt. Vi starter med udgangspositionen AB. Ifølge Archimedes er det fælles tyngdepunkt T₁ sådan beliggende på liniestykket AB, at T₁B/T₁A = mk/m = k. Af formlen ovenfor følger så, at

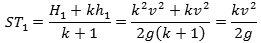
Så tager vi positionen CD. Hvis de to legemer er placeret i C og D, bestemmes deres fælles tyngdepunkt som før. Formlen ovenfor giver så, at

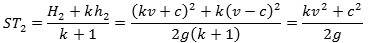
Heraf ses, at tyngdepunktet alt i alt har bevæget sig opad, i modstrid med Torricellis princip. Vores antagelse må derfor være forkert. Efter stødet bevæger den røde kugle sig altså med hastigheden -v, og da den relative hastighed bevares, må den blå kugle efter stødet bevæge sig med hastigheden kv. Hermed er sætningen bevist. Huygens bruger her Torricellis princip på to legemer, som ikke just er mekanisk forbundne, men hvor det enes beliggenhed ikke desto mindre bestemmer det andets. Det er nok en generalisation, som Torricelli ikke selv havde tænkt på, men det er korrekt nok.

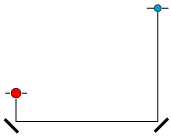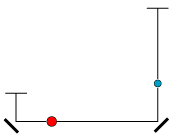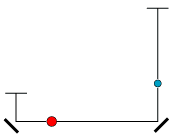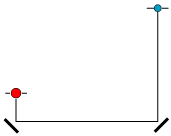Animationen til venstre viser et eksempel. Den røde kugle vejer dobbelt så meget som den blå, så k = 2. Derfor skal den blå kugle før stødet bevæge sig dobbelt så hurtigt som den røde, og den skal så, ifølge Galilei, falde fire gange så langt. Tyngdeakcelerationen er ikke, hvad den plejer at være. Som man ser, bevæger kuglerne sig efter stødet lige så hurtigt som før, men selvfølgelig i modsat retning.

5. Hovedsætningen

Vi er nu kommet så langt, at vi kan behandle stød mellem legemer med vilkårlige masser og vilkårlige hastigheder. Da det generelle tilfælde er noget kompliceret, starter vi med et konkret tilfælde. Vi vil finde ud af, hvad der sker, når en kugle med masse 5 kg og hastighed 2 m/sek støder ind i en kugle med masse 1 kg og hastighed 3 m/sek.

Man kan forholde sig på to måder til diagrammet til højre. Først rent formelt: Da begyndelseshastighederne er omvendt proportionale med masserne, følger A-linien af sætning 3. Og så følger B-linien altid af A-linien, og resultatet er altså, at begge kugler bevæger sig til højre efter stødet med hastigheder på henholdsvis 1/3 m/sek og 16/3 m/sek. Færdigt arbejde. Og så mere eftertænksomt: Min ungdoms højtelskede foresatte skrev i sin disputats:"En matematisk sætning er kun helt tilfredsstillende bevist, når det er muligt at overse betydningen af hvert enkelt led i beviskæden". Og sådan er det jo ikke her. Hvor kommer de mærkelige brøker i A-linien før stødet og i bådens hastighed fra? Jo, hvis man vil bruge sætning 3, skal man jo starte med to hastigheder af formen x og 5x. Så skal man addere den ukendte bådhastighed y, og resultaterne skal så være de to hastigheder i B-linien før stødet. Det giver to ligninger med to ubekendte til bestemmelse af x og y. Sådan fandt jeg dem her, og sådan kan de findes i det generelle tilfælde.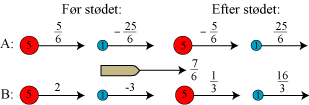

Men inden vi går videre til det generelle tilfælde, vil vi nævne en vigtig konsekvens af det eksempel, vi lige har gennemgået. Når et legeme med masse m bevæger sig med farten v, kaldes produktet mv for legemets bevægelsesmængde. Descartes mente, at den samlede bevægelsesmængde ikke ændrer sig under et stød. Eksemplet ovenfor viser, at denne opfattelse er forkert. Bevægelsesmængden før stødet er nemlig 13, mens den efter stødet er 5/3 + 16/3 = 7. Hvis man i forbindelse med et stød ændrer definitionen af bevægelsesmængde, således at v i produktet mv skal betyde den med fortegn regnede hastighed, så bevares bevægelsesmængden i eksemplet ovenfor. Nedenfor viser vi, at sådan forholder det sig altid ved det fuldstændig elastiske stød.

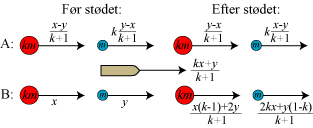
Vi går nu over til det generelle tilfælde, hvor to kugler med vilkårlige masser km og m inden et stød bevæger sig med hastigheder x og y. Vi stiller os den opgave at udregne hastighederne efter stødet. I linie A har vi valgt hastigheder, som er omvendt proportionale med masserne. Hastighederne efter stødet kan derfor bestemmes ved hjælp af sætning 5. De mærkelige begyndelseshastigheder og bådhastigheden er valgt som illustreret i eksemplet ovenfor. I linie B får vi så begyndelseshastighederne x og y, og hastighederne efter stødet kan aflæses i linie B. Vi har altså vist følgende

Hovedsætning: Når to legemer med masserne km og m og hastighederne x og y støder sammen, får de efter stødet hastighederne

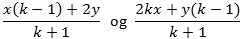
6. To konsekvenser af hovedsætningen

Ved hjælp af hovedsætningen kan vi nu vise, at to almene fysiske sætninger gælder for det fuldstændig elastiske stød:

Bevægelsesmængdesætningen: Summen af produkterne af masse og hastighed er den samme før og efter stødet.

Energisætningen: Summen af produkterne af masse og hastighedskvadrat er den samme før og efter stødet.

Huygens havde ikke begrebet energi til rådighed. Men han opdagede altså, at der var "noget", der var konstant.

Beviset for bevægelsesmængdesætningen foregår ved mekanisk udregning: Før stødet er bevægelsesmængden mkx+my, og efter stødet er den

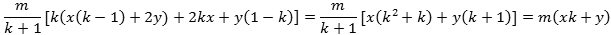
Hermed er bevægelsesmængdesætningen bevist. Ved en tilsvarende udregning kan man bevise energisætningen, men der er det lettere at gå således frem. Vi betragter situationen på figuren nedenfor:

Af sætning 4 fås, at

og bevægelsesmængdesætningen siger, efter bortforkortning af m, at

Ved multiplikation af disse ligninger fås, at

og hermed er energisætningen bevist.

Dette er vist første gang i verdenshistorien, at nogen har opdaget, at produktet af et legemes masse og dets hastigheds kvadrat har en særlig betydning. Det er det, vi i dag kalder bevægelsesenergi, men begrebet energi kendtes ikke dengang, og specielt kendte man ikke begrebet varmeenergi. Huygens var jo godt klar over, at ved et uelastisk stød kunne bevægelsesenergien helt forsvinde, men tiden var ikke moden til at man kunne formulere den generelle sætning om energiens konstans.

7. Konklusion

Man kunne undre sig over, at Huygens kastede sig over det fuldstændig elastiske stød. Den eneste væsentlige viden, man på den tid havde om legemers bevægelse, var Galileis faldlov og hans beskrivelse af kastebevægelsen. Sit forskningsobjekt valgte Huygens efter et meget anbefalelsesværdigt princip: Han valgte et uløst problem, som det lå inden for hans rækkevidde at løse. Han kunne også have prøvet at finde ud af, hvorfor en snurretops akse, foruden rotationen om sig selv, også kan bevæge sig i langsom rotation på en kegleflade, men det holdt han sig fra. Det lå ikke inden for tidens muligheder. Descartes derimod ville forklare hele verdensmekanikken ved at se den som udtryk for små kugler i stadig vekselvirkning. Et håbløst projekt.

De resultater, som vi har nævnt her, er alle fundet af Huygens. Et centralt hjælpemiddel er relativitetsprincippet, som Huygens behandlede ved at tænke sig den båd, der optræder i et flertal af argumenterne ovenfor. Så beviserne skyldes Huygens, men fremstillingsformen er moderne. Vores væsentligste kilde har været A. Ziggelaar: "Christiaan Huygens Dynamiske Grundprincipper og de Anvendelser, Han Gjorde Deraf", Fysisk Tidsskrift 1958. Huygens brugte ikke formelsproget og han brugte ikke talværdier. I stedet han talte om forhold, f.eks. mellem to masser eller to hastigheder. Huygens fandt ikke selv resultaterne i den rækkefølge, som de optræder i her. Rækkefølgen her, som stort set følger "De motu corporum ex percussione", er bestemt af Huygens´ ønske om at vise, at Descartes´ stødteori er forkert ved at slutte det ud fra aksiomer, som Descartes selv måtte anerkende.

Hvis du støder på et ord, hvis betydning du ikke kender, så søg på ordet.