Forside Søgning Liste

Hvis man starter to ens meterlange penduler samtidig, det ene med 5 graders udsving og det andet med 10 graders udsving, så vil man se, at de svinger i takt. Det tager altså samme tid for et pendul at svinge 5 grader som at svinge 10 grader. Men hvis man ændrer de 10 grader til f.eks. 80 grader, kommer de hurtigt ud af takt. Det tager længere tid for et pendul at svinge 80 grader end 5 grader. En kilde fra Science Museum i London oplyser, at hvis man i et pendulur ændrer udsvinget fra 2° til 3°, da bevirker det et tab på 8 sekunder i døgnet.

Når udsvingene er små, er svingningstiden for et pendul altså uafhængig af udsvingets størrelse. Læs om det i 1657 Huygens. Det var, da man havde erkendt dette noget overraskende faktum, at man begyndte at lave pendulure. Her styrer et pendul, hvor hurtigt uret går. Tankegangen er følgende: Man kan ikke helt undgå, at et penduls udsving i tidens løb ændrer sig en lille smule. Der kan komme lidt skidt i maskineriet. Den kæde, som et lod hænger i, bidrager mere til vægten, når loddet er langt nede, end når det er oppe. Og en fjeder, der er lige ved at løbe ud, trykker nok lidt mindre, end når den er stram. Disse fejlkilder kan man altså være ligeglad med, sålænge udsvingene er små.

Men derfor kunne man jo godt stille sig selv den opgave at indrette et pendul, så svingningstiden er uafhængig af udsvingets størrelse også for store udsving. Huygens stillede sig selv den opgave, og han løste den. Vi går nu over til at beskrive Huygens resultat. De tilhørende udregninger er dog her beskrevet i moderne sprog.

1. Huygens´ arbejde med en cykloideformet skål

Hvordan Huygens fik ideen ved vi ikke, men han fik altså den ide at kigge på en cykloide. En cykloide er den kurve et punkt på en cirkel beskriver, når cirklen ruller på en ret linie: På animationen nedenfor ruller den røde cirkel på den sorte linie. Og det fremhævede røde punkt på cirklen beskriver så den blå cykloide:

Hver gang det røde punkt er nær den sorte linie, dannes der en spids på cykloiden. Vi får kun brug for det stykke af cykloiden, der ligger mellem to nabospidser. Og vi får brug for at vende op og ned på det, sådan som det er vist på figuren nedenfor:

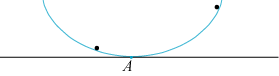
Vi tænker os, at figuren forestiller en cykloide, der er et lodret snit i en glat skål, der står på et bord. Så tager vi to små glatte sorte kugler, dem holder vi fast i skålen i forskellig højde. Huygens fantastiske opdagelse er nu følgende:

Man må forvente, at en så overraskende og kompliceret påstand kræver et noget kompliceret bevis. Her bruger vi differentialregning, som Huygens ikke havde til rådighed, men alligevel er det kompliceret. På figuren tænker vi os, at den røde cirkel starter med at røre X-aksen i punktet O, og at den så ruller til venstre. P er det punkt på cirklen, der var i O til at begynde med. På figuren viser vi situationen, hvor cirklen har drejet sig (rullet) så meget, at vinklen ORP har fået størrelsen v.

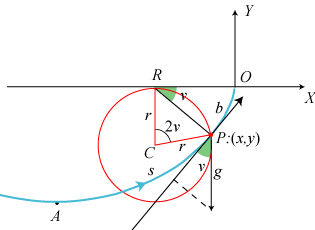Vi starter med ren matematik. Vi vil finde buelængden b af cykloidebuen mellem O og P udtrykt ved drejningsvinklen v og cirklens radius r. For at kunne gøre det er vi nødt til først at finde en parameterfremstilling for cykloiden. Vi vil bruge drejningsvinklen v som parameter. Vi skal altså finde koordinaterne (x,y) til P udtrykt ved r og v. Først udtrykker vi vektoren OP ved tre andre vektorer: OP = OR + RC + CP I koordinater bliver det (x,y) = (-2rv,0) + (0,-r) + r (cos(π/2-2v),sin(π/2-2v)) = r(sin 2v - 2v, cos 2v - 1), 0≤v≤π Hermed har vi fundet en parameterfremstilling for hele cykloidebuen. På figuren har vi også tegnet tangenten til cykloiden i punktet P. Da bevægelsen i det betragtede øjeblik er en rulning om R, er tangenten vinkelret på RP. Den grønne drejningsvinkel v findes derfor to steder på figuren. Vi kan nu gå over til at bestemme buelængden b. Vi bruger Newtons notation og lader prik over betyde differentiation mht. v. Så får vi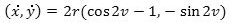

Nu bruger vi så den buelængdeformel, som vi har vist i 1670 parameterfremstilling til beregning af b:

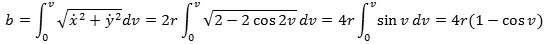
Ved at sætte v = π/2 får vi, at buen AO har længden 4r. Heraf følger, at buen fra A til P har længden s = 4rcosv.

Nu kommer der mere fysik ind i billedet, så vi tænker os, at P er en glat kugle, der glider nedad i skålen.

Til slut i siden om parameterfremstilling har vi vist, at d²s/dt² er den med fortegn regnede længde af accelerationens projektion på tangenten. Accelerationen af P skyldes to kræfter: Trykkraften fra skålen og tyngdekraften. Trykkraften fra skålen er vinkelret på skålen. Det bidrag til accelerationen, som denne kraft giver, er derfor vinkelret på tangenten. Det er derfor kun tyngdeaccelerationen, der bidrager til accelerationens projektion på tangenten. Projektionen er - gcosv = - gs/4r. Bevægelsen af P bestemmes derfor af følgende differentialligning af 2. orden:

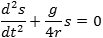
I vores omtale af differentiation har vi nævnt, at når man sætter

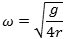
da er samtlige løsninger til differentialligningen

s(t) = a·cosωt + b·sinωt

Her er a og b to tal, hvis værdier afhænger af, hvor højt oppe i skålen vi starter P, og af hvilken begyndelseshastighed vi giver P. s(t) varierer altså sinusformet med vinkelfrekvens ω og svingningstid T = 2π/ω. Og her er så hovedresultatet:

Svingningstiden er den samme uanset hvor i skålen vi lægger P til at begynde med.

Hvis begyndelseshastigheden for P er 0, er b = 0. Det ser man ved at finde hastigheden af P, og det gør man ved at differentiere formlen for s(t). Derfor er s(t) = a·cosωt. P når bunden, når s(t) første gang bliver 0. Det sker, når ωt = π/2 dvs. når

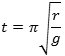
Så lang tid tager det altså for kuglen at nå ned til bunden af skålen, uanset hvor den sættes i gang.

2. Huygens´ arbejde med ligetidige penduler

Nu havde Huygens opdaget, at en kugle i en cykloideformet skål udfører svingninger med en periode, der er uafhængig at startpositionen. Han ønskede nu at omsætte denne opdagelse til et pendul med tilsvarende ligetidige svingninger. Og der kom naturen - eller hvem det nu er - på forunderlig måde til hjælp. Han opdagede nemlig, at et sådant pendul kunne indrettes med tre cykloider.

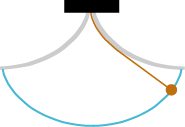Vi viser konstruktionen på billedet. Der er et brunt pendul og to tykke buede metalplader ophægt i det sorte loft. Metalpladernes undersider har form som to ens halve cykloidebuer, der mødes i en spids i midten. Pendulets længde, målt til centrum forneden, er lig længden, af en af de grå cykloidebuer. Pendulet er ophængt i en snor, der under pendulsvingningen lægger sig et kortere eller længere stykke op ad de grå plader. Der gælder så den mærkelige og overraskende sætning, at pendulets centrum bevæger sig på den blå cykloide, hvis halvdele er magen til cykloidebuerne ovenfor. Beviset er ren matematik, så det tager vi ikke her. Da det ikke gør nogen forskel, om pendulet tvinges til at følge cykloiden af en skål eller af en snor, er svingningerne ligetidige. Pendulet har altså samme svingningstid, hvad enten det maksimale udsving er stort eller lille. Konklusion: Når pendulet på figuren er ophængt mellem to cykloideformede skærme, bevæger det sig selv på en cykloide, og svingningstiden er uafhængig af udsvingets størrelse

På billedet til højre viser vi en tegning af et af de ure, som Huygens konstruerede. Pendulet er ophængt mellem de to buede plader, som er betegnet K foroven i midten og til højre på figuren. De er formet som cykloidebuer med spids i ophængningspunktet. Huygens kunne nøjes med små cykloidestykker, da pendulet kun havde små udsving. Pendulet svinger derfor ligetidigt, også selv om de små slag fra urværket, som vedligeholder svingningerne, kan variere lidt i styrke. Du kan læse udførligt om dette urs konstruktion under 1657 Huygens. Teoretisk er denne pendulkonstruktion af Huygens af stor interesse, og ideen bag er helt vidunderlig - hvis man er til den slags ting. Men såvidt vi ved, spillede den i praksis ingen rolle. Det var andre fejlkilder, der bestemte hvor nøjagtigt samtidens ure gik. Og når man kunne nøjes med små udsving, har penduler med cirkelformede udsving også ligetidige svingninger, se 1657 Huygens. Så det her er et af mange eksempler på, at teorien overhaler virkeligheden.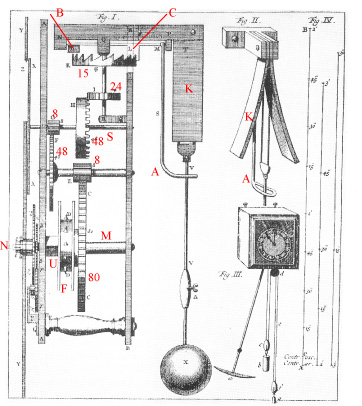

Hvis du støder på et ord, hvis betydning du ikke kender, så søg på ordet.