Forside Søgning Liste

Kepler arbejdede som assistent hos Tycho Brahe i de sidste 18 måneder af Tycho Brahes liv. Her lærte Kepler Tychos store observationsmateriale at kende, og efter Tycho Brahes død fortsatte Kepler med at bearbejde materialet. Det var Keplers projekt at benytte Tycho Brahes meget omfattende observationsmateriale til at bestemme, hvordan planeterne bevæger sig. Udgangspunktet var, at Solen står stille, og at Jorden bevæger sig i en cirkelformet bane om Solen. Kepler udførte det ved beregning, men her vil vi kort forklare hans metode geometrisk.

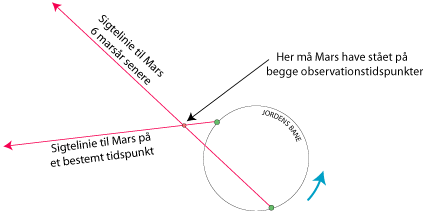
Kepler ledte i Thycho Brahes observationsmateriale efter to marsobservationer, der var foretaget med et mellemrum, der var et helt antal marsår. På disse tidspunkter stod Mars i samme position i sin bane, mens Jorden står i to forskellige positioner i sin bane. På figuren ovenfor har vi indtegnet Jorden i sine to positioner samt retningerne af de to sigtelinier fra Jorden til Mars, som Tycho Brahe havde bestemt. Mars må da på begge observationstidspunkter have befundet sig, hvor sigtelinierne skærer hinanden. Ved at finde mange sådanne par af observationer, kunne Kepler bestemme ligeså mange punkter af marsbanen og derved bestemme både banens form, og hvordan Mars bevæger sig i sin bane. Tilsvarende behandledes de andre planeter. På baggrund af disse beregninger nåede Kepler frem til sine berømte tre love for planetbevægelserne.

Keplers 1. lov

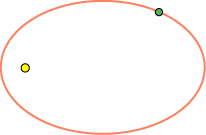
Planetbanerne er ellipser med Solen i det ene brændpunkt. På figuren ovenfor viser vi en planetbane. Fladtrykningen er nu overdrevet, det minder mere om en kometbane.

Keplers 2. lov

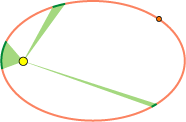
Under en planets bevægelse vil liniestykket mellem planeten og Solen overstryge lige store arealer i lige lange tidsrum. På figuren er de tre lysegrønne arealer lige store. Derfor er planeten lige lang tid om at gennemløbe de tre mørkegrønne buer. Planeten bevæger sig altså hurtigst, når den er nærmest Solen. Man kalder det areal, der overstryges på en tidsenhed, for arealhastigheden. Planetbanerne er så nær ved at være cirkler, at man på en animation her ikke ville kunne se hastighedsvariationen. Men det kan man på en kometbane. Herunder viser vi, hvordan bevægelsen af Halleys komet (lilla) og planeten Saturn (grøn) ser ud; Solen er den lille gule cirkel til venstre i banen og Jordens bane er tegnet ind med blåt:

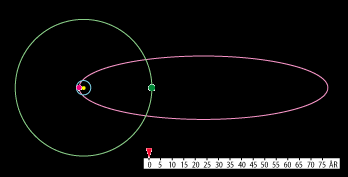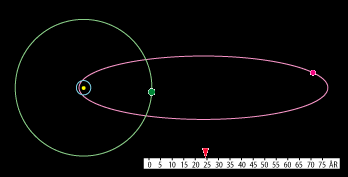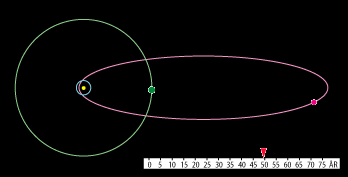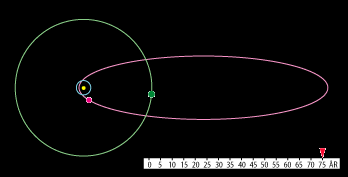
Bevægelsen tænkes set fra Ekliptikas nordpol. Halleys komet har retrograd bevægelse. Den bevæger sig modsat rundt i forhold til planeterne. Der er ingen risiko for sammenstød, for de to baneplaner er vippet lidt i forhold til hinanden. Med figurens målestok vil den nærmeste stjerne være 650 meter væk, så det er ikke sådan, at kometerne bevæger sig rundt mellem stjernerne. På animationen har himmellegemerne overdrevne størrelser. Solen er langt den største af de tre. For at få en periodisk animation har vi sat Saturns omløbstid til 25 år. I virkeligheden er den 30 år.

Keplers 3. lov

siger, at forholdet mellem omløbstiden O i anden potens og middelafstanden A til Solen i tredie potens, altså O²/A³, er det samme for alle planeter.

Det var først Newton, der udledte lovene af generelle fysiske principper.

Det var et resultat af Keplers arbejde, at man fik pålidelige værdier for planeternes middelafstande fra Solen målt med jordbanens radius som enhed. Denne enhed for afstand kaldes en astronomisk enhed og betegnes AE. I dag ved vi, at 1 AE = ca.150 millioner km. Resultaterne kan ses i nedenstående tabel, hvor middelafstanden A fra Solen måles i astronomiske enheder og omløbstiden O i år. I tabellen angiver vi også planetbanernes excentricitet e, se evt. keglesnit samt baneplanernes hældning v i forhold til ekliptikas plan. - Det var ikke alle tallene, der var kendt på Keplers tid. I de sidste to linier i tabellen illustrerer vi Keplers tredie lov. Med de anvendte enheder siger Keplers tredie lov, at A3 = O2 fordi det for Jorden gælder, at A = 1 og O = 1. MERKUR VENUS JORDEN MARS JUPITER SATURN URANUS NEPTUN PLUTO A 0,387 0,72 1 1,52 5,2 9,55 19,2 30,1 39,5 O 0,241 0,616 1 1,88 11,9 29,5 83,7 165 249 e 0,206 0,007 0,017 0,09 0,048 0,056 0,046 0,0097 0,2482 v 7° 3,39° 0° 1,85° 1,3° 2,49° 0,77° 1,77° 17° A3 0,0580 0,373 1 3,51 141 871 7080 27300 61600 O2 0,0581 0,379 1 3,53 142 870 7005 27200 62000 Excentriciteten e er et mål for graden af fladtrykthed, den ligger mellem 0 og 1. Excentriciteten er nær 0 for ellipser, der næsten er cirkelformede og nær 1 for meget fladtrykte ellipser. Den mest fladtrykte planetbane er Plutos med en ekcentricitet på e = 0,248. 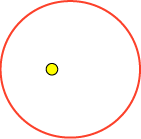Plutos bane ser således ud: Man kan næsten ikke se, at den er en ellipse, men hvis din skærm ikke har mishandlet figuren, måler den 2 mm mindre i højden end i bredden. Derimod kan man tydeligt se, at brændpunktet er flyttet væk fra centrum. De andre planetbaner er endnu mindre fladtrykte. 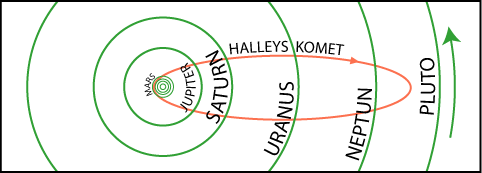På figuren viser vi de relative størrelser af planetbanerne. Vi viser også Halleys Komets bane; den er meget excentrisk, det er de fleste kometbaner. Det vidner om kvaliteten af Keplers arbejde, at Keplers tre love alene bestemmer, hvilke planetbaner, der er mulige, og hvordan planeter kan bevæge sig: 1. lov siger nemlig, at banen må være en ellipse. Og når den er valgt, bestemmer 3. lov omløbstiden O ved sammenligning med Jorden. Hvis ellipsens areal er E er arealhastigheden E/O, og når den er kendt, ved vi fra 2. lov, hvor hurtigt planeten bevæger sig i hvert punkt af ellipsen. Keplers tre love bestemmer altså præcist, hvordan planeter og asteroider og periodiske kometer kan bevæge sig. Opgave 1 Under omtalen af Kopernikus (1543) forklarede vi, at de ydre planeters retrograde bevægelser er en naturlig følge af det kopernikanske verdensbillede. Derimod oplyste vi ikke, om det er et tilfælde, at alle de ydre planeter har retrograde bevægelser. Kunne der godt have været en ydre planet uden retrograd bevægelse? Vi overlader besvarelsen af dette spørgsmål til læseren som en opgave. På baggrund af sine resultater forudsagde Kepler venuspassager, dvs situationer hvor Venus set fra Jorden bevæger sig ind foran solskiven og ses som en lille sort prik på solskiven. Kepler forudsagde en venuspassage i 1639, men han døde jo i 1630, så han så den ikke selv, men det var der en engelsk amatørastronom, der gjorde. Senere har der været venuspassager i 1761, 1769, 1874, 1882, 2004 og 2012. Den næste kommer i 2117. Passagerne i 17-hundredetallet blev af stor betydning. Venus er den planet, der kommer nærmest Jorden. Men når Venus er nær Jorden, kan den normalt ikke ses, fordi den på himlen står lige ved siden af Solen. Kun når der er venuspassage kan Venus ses, når den er nær ved Jorden. I sidste halvdel af 1700-tallet brugte man de to nævnte venuspassager til bestemmelse af afstanden til Venus. Metoden lignede den, Cassini brugte til bestemmelse af afstanden til Mars, men nøjagtigheden blev større, fordi Venus kommer nærmere Jorden end Mars. Systemet i venuspassagerne er, at når der endelig er en, så kommer der en til 8 år senere. Der er skiftevis ca 105 år og ca 121 år mellem parrene. Venuspassagerne finder altid sted ca 8. december eller ca 7. juni. Mystisk ikke?, men sådan er det, og det kunne Kepler altså regne ud. Kepler beregnede også en kometbane, men han fandt, at den var retlinet. Den første ellipseformede kometbane blev beregnet af Halley i 1682. Efter at have læst William Gilberts "Om Magneter" (1600), besluttede Kepler sig til at tro, at en eller anden kraft udgår fra Solen og påvirker planeterne (herunder Jorden) og får dem til at gå rundt i deres bane. Det forklarer også, at Solens kraft, ligesom den magnetiske kraft, bliver mindre, når afstanden bliver større. Planeternes hastighed er derfor mindre ved en større afstand. Hvis du støder på et ord, hvis betydning du ikke kender, så søg på ordet.