Forside Søgning Liste

1. Øjet som optisk instrument

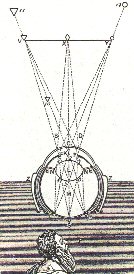Kepler var den første, der forstod, at der i øjet dannes et omvendt billede af synsfeltet på nethinden. Han kunne naturligvis ikke vide, hvordan synsindtrykkene kommer videre til hjernen. Han vidste også godt, at øjet kan akkomodere, dvs danne skarpe billeder af genstande i forskellige afstande. Han troede imidlertid fejlagtigt, at akkomodationen blev tilvejebragt ved at øjet blev mere eller mindre langstrakt. Faktisk er det øjets linse, der kan ændre krumning, så der dannes et skarpt billede på nethinden. Det blev først opdaget senere, se 1611 Scheiner.

2. Totalrefleksion

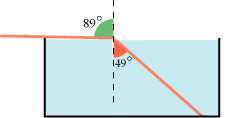
Det følgende kræver kendskab til brydningloven, læs om den under Snell. Figuren nedenfor til venstre viser en næsten vandret lysstråle, der rammer vandoverfladen, hvor det punkterede indfaldslod er tegnet. Da vands brydningsforhold er 1,33 bestemmes den røde brydningsvinkel v af ligningen sin 89°/sin v = 1,33. Ved udregning fås, at v = 49°. Man kan derfor ikke sende en lysstråle ned i vand, så brydningsvinklen bliver større end 49°.

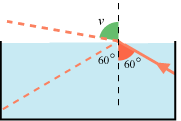
Men strålegangen kan vendes. Den tegnede stråle er der ikke noget problem med, men man får et alvorligt problem, hvis man sender en lysstråle nedefra op mod vandoverfladen, og den røde vinkel er f.eks. 60°, sådan som det er vist på figuren ovenfor til højre. Brydningsforholdet ved overgang fra vand til luft er 3/4 = 0,75, nemlig det reciprokke af forholdet ved overgang fra luft til vand. Brydningsvinklen v bestemmes derfor af ligningen sin 60°/sin v = 0,75. Da sin 60°=0,866, bliver sin v = 0,866/0,75 =  1,15, desværre, for sinus kan aldrig blive større end 1. Brydningsformlen giver altså ingen mening i dette tilfælde, og det var Kepler, der fandt ud af, at strålen i stedet opfatter vandoverfladen som et nedadvendt spejl. Strålen sendes altså ned i vandet, sådan som det er vist punkteret på figuren ovenfor til højre. Man kalder fænomenet totalrefleksion. Den vinkel, hvis sinus er 0,75, er 48½°. Så der er totalrefleksion, når man nedefra sender en lysstråle skråt op mod en vandoverflade, sådan at indfaldsvinklen er større end 48½°. Der er ikke noget at sige til, at det var svært at opdage dette begreb. Det er jo de færreste, der en stille nat lægger sig ned på bunden af en sø med en lommelygte, for at undersøge hvor lysstrålen bliver af, når man lyser skråt op mod undersiden af vandoverfladen.

Nedenfor illustrerer vi fænomenet med en animation. Det er et kar med vand, og lysstrålen kommer nedenfra. Den drejer sig med konstant vinkelhastighed frem og tilbage. På et tidspunkt stopper vi animationen nogle sekunder, for at vise den springvise overgang fra totalrefleksion til brydning.

Lyset kommer her nede fra

"Springvise" skrev vi ovenfra. I fysik vil man normalt tale om en diskontinuitet. Det ord bruger man, når man påvirker et system på en jævn måde, og systemet på et tidspunkt i løbet af ingen tid skifter mellem to helt forskellige tilstande. På animationen ovenfor er den jævne påvirkning den jævne bevægelse af lysstrålen. I det øjeblik, hvor indfaldsvinklen passerer 48½°, skifter den sidste del af strålen fra at være vandret til at gå 48½° skråt nedad. Sådanne diskontinuiteter er sjældne i den klassiske fysik

I denne forbindelse kunne man med vore dages viden spørge, om der slet ingen tilbagekastning sker, når strålen brydes. Svaret er, at når strålen udsendes temmelig lodret, er der en svag tilbagekastning fra undersiden af vandoverfladen på få procent af lysenegien. Først når strålen er meget nær den kritiske vinkel stiger tilbagekastningen noget, og så snart den kritiske vinkel er passeret, er tilbagekastningen 100%.

Figuren nedenfor viser en af konsekvenserne af totalrefleksion, et såkaldt fiskeperspektiv. Øverst vises en lille spejlblank sø Der ligger et par sten på bunden, og der sejler en båd. På bredden ligger en rød kugle,og Solen skinner over det hele.

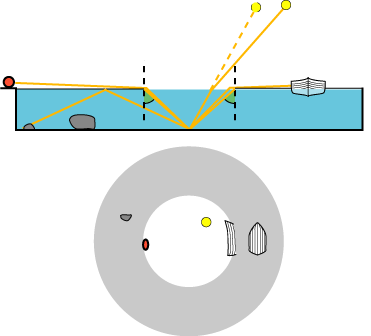
Den nederste del af figuren viser hvordan det hele ser ud for en iagttager, der ligger på bunden midt i søen og kigger op mod vandoverfladen. Bådens underside og den store sten kan ses direkte, og skråt oppe ses spejlbilledet af den lille sten. Det, der er over vandet, kan kun ses gennem et cirkulært "hul" i vandoverfladen. Uden for hullet kan man ikke se gennem vandoverfladen, den er et spejl, hvori tingene på bunden spejler sig. Vinkeldiameteren af hullet er 97°. Til venstre i kanten af hullet ses den røde kugle, noget fladtrykt, og til højre i kanten af hullet ses det øverste af båden. Man kan også se Solen, men dens stilling på himlen er ikke korrekt. På billedet nedenfor viser vi la Cours fiskeperspektiv.

3. Begrebet belysning

På Keplers tid var begrebet belysning (belysningsintensitet) ikke veldefineret. Ikke desto mindre nåede Kepler til en intuitiv forståelse af, hvordan den belysning, som en punktformet lysgiver giver en plan flade, afhænger af afstanden til lysgiveren.

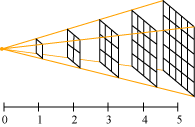
Hvis vi løst sagt definerer belysningen som "lysmængden pr arealenhed", ser man af figuren ovenfor, at belysningen er omvendt proportional med kvadratet på afstanden. F.eks. er belysningen i 4 meters afstand 16 gange så lille, som den er i 1 meters afstand.

Hvis du støder på et ord, hvis betydning du ikke kender, så søg på ordet.