Forside Søgning Liste

1. Indledning

Den første brug af noget, der ligner et koordinatsystem, findes i Descartes´ bog Géométrie fra 1637. Descartes tilpassede sit koordinatsystem til det problem, han skulle løse. Hans koordinatsystemer var ikke retvinklede. I de følgende årtier udvikledes koordinatsystemet som redskab til løsning af geometriske problemer, og omkring 1660 stod koordinatsystemet til rådighed som et magtfuldt redskab både i matematik og fysik. Her vil vi ikke gå nærmere ind på koordinatsystemets historie, men give en kort introduktion til begrebet.

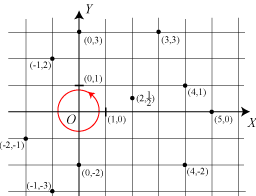
Her viser vi et sædvanligt retvinklet koordinatsystem. Det består af to på hinanden vinkelrette akser, X−aksen og Y−aksen. De skærer hinanden i et punkt O, der kaldes koordinatsystemets begyndelsespunkt. På hver akse er der valgt en enhed fra O og ud til det korte tykke liniestykke vinkelret på aksen. I matematik bruger man normalt samme enhed på de to akser. I fysik giver det ingen mening at tale om samme enhed, hvis de to størrelser, der afsættes ud ad akserne, har forskellig dimension, f.eks tid og temperatur i en vejrudsigt. Hvert punkt i XY−planen har et koordinatsæt (x,y). x er punktets afstand fra Y−aksen, og y dets afstand fra X−aksen. Afstandene regnes med fortegn, sådan som det er vist på figuren. Fidusen ved koordinatsystemet er, at man, i stedet for at arbejde med punkterne, kan regne med koordinaterne. XY−planen orienteres mod uret, dvs fra den positive X−akse mod den positive Y−akse, sådan som det er vist på den røde cirkel. Vinklen fra X−aksen til Y−aksen bliver så +90°, og vinklen fra Y−aksen til X−aksen bliver −90°.

2. Ligningen for en ret linie

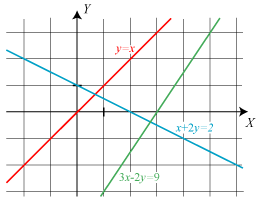
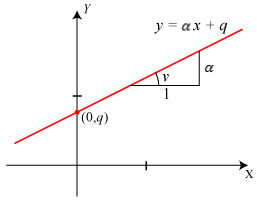
Den grønne linie på figuren har ligningen 3x−2y = 9. Det betyder, at punkterne på linien er de punkter, hvis koordinater (x,y) passer i ligningen. F. eks. ligger punktet (5,3) på linien, og det passer med, at 3·5−2·3 = 9. Prøv eventuelt selv med flere punkter. Skæringspunktet (x,y) mellem den røde og den blå linie er det punkt, hvis koordinater passer i begge ligninger: x+2y = 2 og y =x . Sættes y=x i den første ligning fås, at 3x = 2, så skæringspunktet får koordinaterne (2/3,2/3). Det smarte ved koordinatsystemet er, at man på denne måde kan regne med liniernes ligninger i stedet for at argumentere geometrisk.	Når en linie ikke er lodret, kan dens ligning skrives på formen y = αx+q. Den skærer Y-aksen i punktet (0,q). α er den tilvækst, som y får, når x får tilvæksten 1, sådan som det er vist på figuren. Når α>0, går linien skråt opad til højre, α<0 betyder, at linien går skråt nedad til højre. Dette vigtige tal α kaldes liniens hældningskoefficient. Det er et mål for, hvor stejl linien er. Når α = 1, danner linien en vinkel på 45° med X-aksen. α er et mål for, hvor meget linien hælder. Hvis vinklen fra X-aksen til linien er v, er α = tan v.	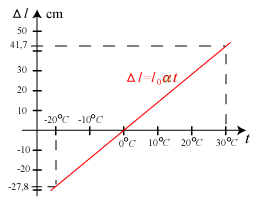Her er et eksempel, der viser, hvordan et koordinatsystem tilpasses til en bestemt anvendelse i fysik. Det handler om længdeudvidelse ved opvarmning. Vi kigger på en stang af et materiale med længdeudvidelseskoefficient α. Hvis den har længden l0 ved 0° C og længden lt ved t° C, gælder, som Ole Rømer fandt ud af, formlen lt=l0(1+αt). Heraf fås, at længdeudvidelsen Δl ved opvarmning fra 0° C til t° C er Δl = lt−l0 = l0αt. Figuren ovenfor viser, hvordan den gamle Lillebæltsbro bliver længere ved opvarmning fra -20° C til 30° C. Længdeudvidelsen for stålet er 0,000118 grad-1, og broen er 1178 meter lang. Læg mærke til, at enhederne på akserne er tilpasset problemet. Umiddelbart kunne man synes, at den linie går sgu stejlt opad, men ved eftersyn af inddelingen på den lodrette akse kan man se, at det ikke er så galt endda. Lillebæltsbroen er ca 70 cm længere på en varm sommerdag end på en kold vinterdag, så afstanden mellem Fyn og Jylland er 70 cm større om sommeren end om vin... . Hm!

2. Ligninger for cirkel, ellipse, hyperbel og parabel

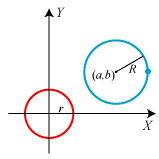
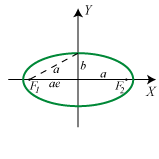
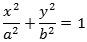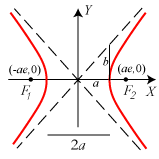
Den røde cirkel har ligningen x2+ y2 =< I>r2. Ifølge Pythagoras udtrykker den jo, at afstanden fra (x,y) til (0,0) er r. Tilsvarende er ligningen for den blå cirkel (x-a)2+(y-b)2= R2. Det passer med, at det viste punkt (x,y)=(a+R,b) ligger på cirklen og passer i ligningen.	Figuren viser en ellipse med halvakser a og b, excentricitet e<1 og brændpunkter F1 og F2. Ligningen for ellipsen er Af den viste trekant får man følgende formel, der sammenknytter excentriciteten e med halvakserne a og b: a2 = a2e2 + b2 Banen for Halleys Komet har en nydelig ellipseform, se under Halley.	Figuren viser en hyperbel med halvakser a og b, excentricitet e>1 og brændpunkter F1 og F2. 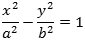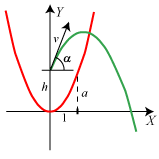Ligningen for hyperblen er Også her gælder følgende formel, der sammenknytter excentriciteten e med halvakserne a og b: a2 = a2e2 - b2 Hyperbler forekommer i naturen, men sjældent. F.eks. er visse kometbaner hyperbelgrene. Et andet eksempel kan du finde under omtalen af en gnomon.	Den røde parabel har ligningen y=ax2. Den grønne parabel er en kasteparabel. Hvis en partikel kastes skråt opad fra det viste punkt på Y-aksen med en starthastighed v, der danner vinklen α med vandret, får den grønne parabel ifølge Torricelli ligningen Minuset viser, at grenene peger nedad, og ved at regne på ligningen kan man besvare spørgsmål om kasteparablen. I mange springvand kan man se nydelige benekurver for vandet. Det var Galilei, der først fandt ud af, at det bliver parabler.

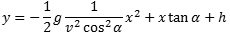Ligningerne ovenfor gælder naturligvis kun, når kurverne ligger på den viste, pæne måde i koordinatsystemet. Men uanset beliggenheden i koordinatsystemet, kan de nævnte kurver altid fremstilles ved en ligning af formen

Omvendt fremstiller en ligning af denne form altid en af de nævnte kurver. (Den kan dog også fremstille to linier, en linie, et punkt eller intet.)

Hvis du støder på et ord, hvis betydning du ikke kender, så søg på ordet.