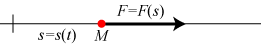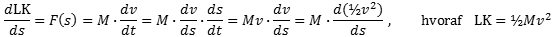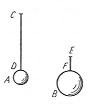
Begreberne bevægelsesmængde (mv) og bevægelsesenergi (½mv²) var i perioden fra Descartes til Euler genstand for ophedede diskussioner. Huygens var klar over, at begge størrelser bevares under et fuldstændig elastisk stød (se 1652 Huygens), men en afklaring af begrebernes betydning skete først langt inde i 1700-tallet.

I 1686 skrev Leibniz en artikel om emnet i tidsskriftet Acta Eruditorum. Titlen var: "A short demonstration of a famous error of Descartes and other learned men, concerning the natural law according to which God always preserves tha same quantity; a law which they use incorrectly, even in mechanics." Vi refererer her kort indholdet af denne artikel.

Artiklen starter med en kritik af Descartes brug af bevægelsesmængde som mål for det, vi i dag kalder bevægelsesenergi, men som på den tid var et noget uafklaret begreb med mange navne: "Vis matrix", "force of bodies in motion", "living force". Vi kalder det her "living force", "levende kraft", selv om Leibniz vist først brugte dette udtryk 10 år senere. Lad os betragte en partikel med vægt M, der bevæger sig med hastighed v. Leibniz definerer så dens levende kraft som det arbejde, der skal udføres for at løfte partiklen så højt op over en vandret plan, at den ender med hastigheden v, når man lader den falde ned igen. Descartes mente at levende kraft kunne måles ved legemernes bevægelsesmængde, dvs. produktet af vægt og hastighed. Leibniz modbeviste dette på følgende måde:

Først antager Leibniz som Huygens, at når et fuldstændig elastisk legeme falder frit fra en bestemt højde, og når der ikke er luftmodstand, så vil legemet, hvis det rammer et hårdt underlag, nå op til samme højde igen. Som Descartes antager Leibniz endvidere, at der skal samme "force" (nærmest vores "arbejde") til at løfte et legeme A, som vejer 1 pund til en højde DC på 4 alen som der skal til at løfte et legeme B, som vejer 4 pund op til en højde EF på 1 alen. (I dag ved vi, at det er rigtigt nok.) Hvis vi nu antager, at A og B fra hvile falder henholdsvis stykkerne CD og EF, så når de ikke ned med samme bevægelsesmængde. For ifølge Galileis faldlov kommer de to legemer ned med hastigheden √(2sg), hvor s er faldvejen og g er tyngdeaccelerationen. Da A falder 4 gange så langt som B, ender A med at have dobbelt så stor hastighed som B. Men B vejer 4 gange så meget som A. Derfor ender B med at have dobbelt så stor bevægelsesmængde som A på trods af, at der er anvendt samme "force" til at få dem i gang. Bevægelsesmængden kan altså ikke bruges som mål for den levende kraft.

I artiklen udtrykker Leibniz også skepsis over et af Descartes (korrekte) resultater om det uelastiske stød. Problemet er, at man på det tidspunkt ikke vidste, at mekanisk energi kan omsættes til varme.

I en senere artikel, "Specimen dynamicum" fra 1695 er Leibniz meget tæt på at finde størrelsen af den levende kraft. Han skriver, at den levende kraft er skabt af uendelig mange påvirkninger fra den kraft, der ændrer legemets hastighed. Med en smule velvilje kan vi i dag fortolke dette på følgende måde:

Vi tænker os, at det røde legeme med vægt M bevæger sig på den vandrette linie, så afstanden til startpunktet til tidspunktet t er s = s(t). Legemet er i hvile til at begynde med. Det er påvirket af en kraft F = F(s), og vi ønsker at finde den levende kraft (altså bevægelsesenergien) LK. Det, som Leibniz skriver må fortolkes som LK = ∑F(s)·ds = ∫F(s)ds , hvor den tilbagelagte vej er opdelt i uendelig mange uendelig små stykker ds. I 1695 havde Leibniz udviklet differential- og integralregningen så meget, at han kunne udføre følgende regninger:

Regningerne står ikke i artiklen, men Leibniz kan ikke have undgået at formulere sin sum som et integral. Han må på det tidspunkt også have kendt Newtons 2. lov, så det er sandsynligt at han har kendt formlen for den levende kraft.

Hvis du støder på et ord, hvis betydning du ikke kender, så søg på ordet.