Marin Mersenne

I 1637 udgav Mersenne en bog med titlen L´Harmonie Universelle. Bogen handler om mange forskellige emner, men 71 sider, fra side 157 til side 228, handler mest om svingende strenge, f.eks. i musikinstrumenter. Afsnittet kaldes på fransk bog 3, og vi viser det øverste af første side af bog 3 herunder. Under billedet er der en oversættelse til dansk af teksten.

Her kommer en oversættelse af det, der står:

Tredie Bog handler om de bevægelser som tryk, tyngdekraft og andre påvirkninger skaber på harmoniske strenge og andre legemer.
Efter at have beskrevet bevægelserne af de vigtigste legemer i dette univers, specielt Jordens bevægelse, vil vi mere omhyggeligt undersøge, hvordan det forholder sig med strenge og andre legemer, der skaber harmoni. Og det er, hvad vi vil gøre, med det vi fremlægger i denne bog, i hvilken vi også vil behandle den kraft, der er nødvendig til at fastholde en given vægt, der befinder sig på en skrå plan, der hælder mod horisonten.
Læresætning 1
Grunden til antallet af svingninger af alle slags strenge er, at antallet er omvendt proportional med strengens længde.

- ja, det var så oversættelsen.

Indenfor fysikken handler Mersennes vigtigste resultat om svingninger af en stramt udspændt streng, sådan som det er vist på figuren til højre. Hvis man anslår strengen svinger den samtidig med en eller flere frekvenser. Frekvensen er antallet af svingninger pr. sekund. Frekvenserne afhænger af tre ting:
1. Længden L af strengen.
2. Størrelsen af den kraft M, der holder strengen stram.
3. Vægten V per længdeenhed af strengen.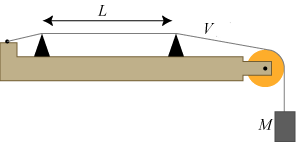

Mersenne angiver, at den mindste af de frekvenser f, som strengen kan svinge med, har følgende tre egenskaber:
1. Som nævnt ovenfor er f omvendt proportional med L. Det betyder, at hvis man gør L dobbelt så stor, bliver f halvt så stor.
2. f er proportional med kvadratroden af M. Det betyder, at hvis man gør M fire gange så stor, bliver f dobbelt så stor.
3. f er omvendt proportional med kvadratroden af V. Det betyder, at hvis man gør V fire gange så stor, så bliver f halvt så stor.

I Mersennes bog har jeg ikke kunnet finde 2. og 3 omtalt, men la Cour bekræfter, at Mersenne havde disse resultater.

Jeg ved ikke, hvor nøjagtige resultaterne er, og jeg ved heller ikke om de er fundet ved iagttagelser eller ved teoretiske beregninger. De tre resultater kan sammenfattes i formlen

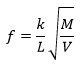
Her betyder k et tal, hvis værdi kan findes ved en enkelt iagttagelse af de 4 variable størrelser. Mersenne skelnede næppe mellem masse og kraft.

Frekvensen f fremkommer, i hvert fald som dominerende, hvis strengen anslås på midten. Frekvensen kaldes grundtonen. Hvis strengen anslås ¼ strenglængde fra en af enderne, bliver den dominerende frekvens dobbelt så stor, i hvert fald, hvis man i anslagsøjeblikket holder midtpunktet i ro. Alt i alt er de frekvenser, som strengen kan svinge med, heltallige multipla af grundtonens frekvens.

La Cour meddeler at Brook Taylor i 1714 fandt Mersennes formel ved teoretiske overvejelser. Han fandt bl.a. ud af, at ved at skelne mellem kraft og Masse bliver k dimensionsløs og faktisk lig med ½, lige meget hvilke enheder, man bruger. Frekvensen bliver derfor bestemt af formlen

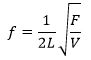
hvor F = M·g er den kraft, som påvirker strengen.

La Cour gennemgår et eksempel hvor han sætter k = 1. Han får derfor dobbelt så mange svingninger pr. sek. som Taylor; grunden kan være, at la Cour definerer én svingning som en bevægelse i én retning, hvor man normalt definerer én svingning som en bevægelse frem og tilbage.

Hvis du støder på et ord,
hvis betydning du ikke kender,
så søg på ordet.