NEWTON OM TYNGDEFELTET OMKRING EN KUGLE

Ind til listen:

Vi bringer her en oversættelse af de sider fra Principia, der handler om tyngdefeltet omkring en kugle. Det er side 193-195 i en version, der ligger på nettet. Oversættelsen er ikke ordret, men jeg har tilstræbt, at den beskriver Newtons tankegang. Figurerne er Newtons egne. Kommentarer fra mig skriver jeg i kantede parenteser. Newtons originale artikel kan du se, ved at klikke her.

Tiltrækningskræfterne fra kugleformede legemer.

Sætning 1

Hvis enhver partikel på en kugleformet overflade påvirker omgivelserne med tiltrækningskræfter, der aftager med kvadratet på afstanden, så vil en partikel P, der ligger inden for kuglefladen, ikke blive tiltrukket af nogen resulterende kraft.

Bevis: Lad HIKL være kuglefladen, og lad P være en partikel inde i kuglen. Gennem P tegner vi to linjestykker HK og IL så der dannes to meget små buer HI og KL. Som før bemærket vil trekanterne HPI og LPK være ligedannede, og derfor vil de små buer forholde sig som afstandene HP og LP.

Vi betragter nu to vilkårlige lige store partikler på henholdsvis HI og KL, som ligger sådan, at linjestykket, der forbinder dem, går gennem P. Tiltrækningerne fra P på disse partikler vil forholde som kvadratet på afstandene ind til P. Derfor vil disse partikler påvirke P med lige store kræfter. For kræfterne er proportionale med masserne og de er omvendt proportionale med kvadratet på afstandene. Tiltrækningerne er altså lige store, og da de er modsat rettede ophæver de hinanden. Da dette gælder for alle tiltrækningerne fra hele den kugleformede overflade. Derfor virker der ingen samlet tiltrækningskraft på P fra kugleoverfladen. Hvilket skulle bevises.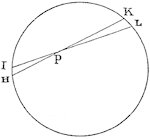

[Det Newton burde beskrive er to områder på kugleoverfladen. De betegnes HI og KL. HI fås af KL ved multiplikation ud fra P med PH/PL. Områdernes masser er proportionale med deres arealer. Newton burde beskrive hvordan hele kuglefladen opdeles i sådanne områder.]

Sætning 2

I fortsættelse af ovenstående vil en partikel placeret uden for kuglen være påvirket af en tiltrækningskraft rettet mod centrum af kuglen, en tiltrækningskraft der er omvendt proportional med kvadratet på afstanden fra centret.

Bevis: På figuren nedenfor viser vi to ens kugler AHKB, ahkb med centre S, s og diametre AB, ab. Lad P og p være to partikler placeret uden for kuglerne på forlængelsen af diametrene. Fra partiklerne tegner vi linjernePHK, PIL, phk, pil. Disse linjer skærer cirklerne AHB, ahb i de lige store buer HK = hk, IL = il. På de nævnte linjer tegner vi vinkelrette fra centrene S, s. De betegnes SD, SE, sd, se. SD og sd skærer PL og pl i F og f

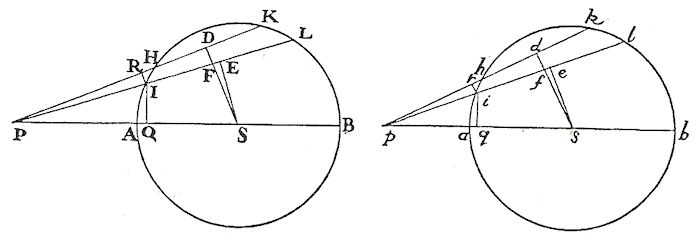
Lad os også nedfælde de vinkelrette IQ, iq. Lad os nu lade vinklerne DPE, dpe gå mod 0. Eftersom DS = ds og ES = es kan man regne med, at PE = PF og pe = pf og også at de korte linjer DF og df kan regnes for at være lige store. Det skyldes, at DPE og dpe går samtidig mod 0. Af dette følger, at

PI:PF = RI:DF og

pf:pi = DF:ri

Hvis vi multiplicerer disse to ligninger får vi

(PI·pf):(PF·pi) = RI:ri = bueIH:bueih

[Det sidste lighedstegn følger ifølge Newton af et tidligere hjælpesætning. Da areal er proportional med masse, skelner vi ikke mellem disse to begreber.] Videre fås, at

PI:PS = IQ:SE og

ps:pi = SE:iq . Ved multiplikation fås,

(PI·ps):(PS·pi) = IQ:iq. Multiplicerer vi denne ligning med den lange formel ovenfor får vi, at

(PI²·pf·ps):(pi²·PF·PS) = (HI·IQ):(ih·iq)

[I det følgnde supplerer jeg Newtons tekst med nye variable og formler, der forhåbentlig øger forståeligheden for læseren.]

Lad nu O betegne arealet af den ringformede figur som beskrives af buen HI, når den drejes 360° om linjen AB og lad o betegne arealet af den ringformede figur som beskrives af buen hi, når den drejes 360° om linjen ab. Så vil O = 2π·IQ·HI og o = 2π·iq·hi. Så vil O:o = (HI·IQ):(ih·iq), altså højre side i formlen ovenfor:

(PI²·pf·ps):(pi²·PF·PS) = O:o.

Lad nu T og U være de kræfter som de to overflader tiltrækker henholdsvis P og p med. Da kræfterne er proportionale med masserne og omvendt proportionale med kvadratet på afstandene vil

T:U = (O:o)·(pi²):(PI²) = (pf·ps):(PF·PS).

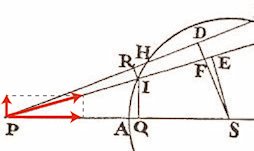Kraften T skulle fra begyndelsen have været opløst i komposanter i retning af PS og vinkelret på denne, sådan som det er illustreret på min figur til venstre. Disse sidste komposanter har samlet ingen virkning på P, så dem kan man se bort fra. Da den trekant, der er bestemt af de to lange røde kræfter, er ensvinklet med trekanterne PIQ og PSF skal den skrå røde kraft T formindskes med faktoren PS:PF. På samme måde kan man vise, at kraften U skal formindskes med faktoren ps:pf.

Af formlen oven for figuren følger nu at

T:U = ((pf · ps):(PS · PF) ) : ((PF · PS):(ps · pf )) = (pf · PF) : (PS · pf ) = pf ² : PS ²

Lad nu O betegne arealet af den ringformede figur som beskrives af buen KL, når den drejes 360° om linjen AB og lad o betegne arealet af den ringformede figur som beskrives af buen kl , når den drejes 360° om linjen ab. Lad også V og W være de kræfter som O henholdsvis o påvirker P og p med. Så kan man på samme måde bevise, at V:W = pf ² : PS ²

Vi deler nu de to kugleflader i en masse par af ringformede overflader som dem ovenfor, idet vi sørger for, at det for hvert par gælder, HK = hk og IL = il. Så vil vi for hvert par få at tiltrækningskræfterne har forholdet pf ² : PS ². [Her har vi brugt det understregede ovenfor.] Ved addition af arealerne af ringene får vi, at de samlede tyngdekræfter på på P og p har forholdet pf ² : PS ². Tyngdekræfterne forholder sig altså omvendt af kvadraterne på afstandene til centrene, hvilket skulle bevises.

[Newton skriver det ikke, men ud fra det beviste er det let at indse, at en massiv homogen kugle påvirker to partikler P og p med tiltrækningskræfter, der er omvendt proportionale med kvadraterne på afstandene fra partiklerne til centrene. Resutatet var vigtigt for fremtidige beregninger af planeternes bevægelser. Det kan udtrykkes på den måde, at man under beregningerne kan antage, at hele Jordens masse er placeret i dens centrum.]

[Newton var genial; jeg forstår godt hans bevis, men jeg forstår ikke, hvordan han har fundet på det.]

Hvis du støder på et ord,
hvis betydning du ikke kender,
så søg på ordet.