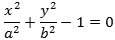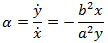|
Forside
Søgning
Liste |  |
Newtons og Leibniz´ differential- og integralregning
1. Indledning
Newton skabte sin version af differential- og integralregningen i årene 1664-1666, de år, der kaldes hans "anni mirabiles", dvs "mirakuløse år". Newtons beskrivelse cirkulerede blandt vennerne i Royal Society, men den blev først offentliggjort mange år senere. Differentialregningen blev til dels beskrevet i Principia i 1687, dog kun i den udstrækning den blev anvendt i fysikken. Integralregningen blev først offentliggjort i 1704. Newtons arbejde vakte kun begrænset opmærksomhed på Kontinentet, dvs uden for England, og selv i England publiceredes der kun lidt i fortsættelse af Newtons arbejde med differential- og integralregningen.
Uafhængigt af Newton skabte Leibniz sin version af differential- og integralregningen i 1675, og han offentliggjorde den i årene 1684-1686. Umiddelbart herefter arbejdede andre matematikere videre i fortsættelse af Leibniz´ arbejde, og der udfoldedes på Kontinentet en livlig publikationsvirksomhed om differential- og integralregning.
Både Newton og Leibniz fandt analysens hovedsætning. Den siger, at differentiation og integration er omvendte regningsarter.
Det betyder, at integralet af differentialkvotienten af en variabel y er y selv, og at differentialkvotienten af
integralet af y også er y selv. Under 1670 Integralregning og 1670 Differentialregning
kan du læse en beskrivelse af sagen, sådan som
den opfattes i dag. Herunder giver vi kortfattede beskrivelser med Newtons og Leibniz´ egne formuleringer.
2. Om Newtons differential- og integralregning.
A. Newtons integraltabel
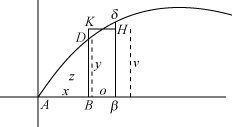 | I sit manuskript "De analysi" fra 1669 bringer Newton en tabel over integraler, - selv om han ikke kaldte det sådan. Newton tager udgangspunkt i figuren til venstre. Tankegangen er følgende: Kurven ADδ er ukendt, men arealet z er valgt, udtrykt ved x. Newton beskriver så ved et eksempel en metode til udregning af y, udtrykt ved x. Newton har nok tænkt , at x er tiden og at y derfor er den hastighed, som z vokser med, når tiden går. I dag vil vi sige, at y er differentialkvotienten af z mht. tiden. Herunder følger en beskrivelse, som er meget tæt på Newtons egen. Det fremgår af beskrivelsen, at Newton var klar over, at differentiation og integration er omvendte regningsarter. Formuleringerne nedenfor er tæt på Newtons egne. |
På figuren er v = BK valgt sådan, at arealet BDδβ = arealet BKHβ = vo. Betragt nu det tilfælde, hvor
 | eller - for at fjerne roduddragningen - |

| Heraf følger, at | 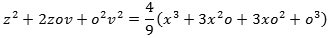 |
| Nu kan man fjerne leddene uden o, og ved derefter at dividere med o får man, at |
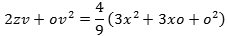 |
| Resultatet er, at | 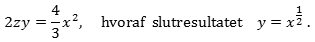 |
Med vore dages sprog har vi fundet differentialkvotienten y = dz/dx og vi har fundet integralet z af y. Det er klart, at metoden altid kan bruges, når z er udtrykt ved x som en sum af potenser og rodstørrelser. Newton brugte metoden på en lang række z-udtryk og fandt hvilket y-udtryk, de var integral af. Newton selv ville sige, at "kvadraturen (dvs. arealet) svarende til kurven y er z."
| F.eks. fandt Newton, at hvis han valgte | 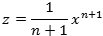
| , da bliver | 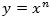 |
| og hvis han valgte | 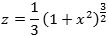
| , da bliver | 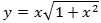 |
| Kurve y | Kvadratur z |
|---|---|
 |  |
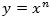 | 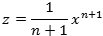 |
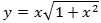 | 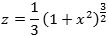 |
| ... | ... |
Det er verdens første tabel over integraler!
B. Newtons fluenter og fluxioner
Newton brugte ordet "fluent" om en størrelse, der varierer i tidens løb. På figuren ovenfor kan vi tænke os, at punktet B bevæger sig på den vandrette akse. Så er y og z fluenter. Hældningen for tangenten til kurven i punktet D er også en fluent. En fluent er altså en variabel, hvis værdi skifter i tidens løb.
Til enhver fluent hører der en anden variabel, der kaldes den tilsvarende fluxion. Fluxionen er den hastighed, som værdien af fluenten ændres med. Hvis fluenten er f.eks x = 3t2 er fluxionen 6t.
| Hvis x er en fluent betegnes dens fluxion | 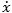 . . |
I vore dages sprog er fluxionen altså dx/dt. Newton behøver ikke i betegnelsen at synliggøre navnet på den variabel, som der differentieres med hensyn til. Alle differentiationer er nemlig mht. tiden. Hvis vi på figuren ovenfor betegner hældningen for tangenten i punktet D med α vil
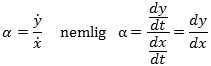
Hvis nu vi ændrer et tidspunkt t til tidspunktet t+o, hvor o er uendelig lille, vil de tilsvarende ændringer af fluenterne x og y være
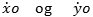
Newton illustrerer i et manuskript fra 1671 hvordan man ud fra en kurves ligning kan finde tangenthældningen α. Han betragter kurven med ligningen
x3 - ax2 + axy - y3 = 0.


De fire førsteled i parenteserne giver et 0. Hvis vi derefter dividerer med o og sletter de led, der stadig indeholder et o, så får vi,
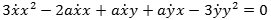
og af denne ligning finder vi endelig hældningskoefficienten α til tangenten i kurvepunktet (x,y):

Læg mærke til, at Newtons metode ikke kræver, at kurvens ligning har formen y = f(x). Metoden kan altså benyttes til tangentbestemmelse for kurver, der ikke er grafisk billede af en funktion.
Lad os nu se hvad Newtons metode giver, når man anvender den på ellipsen med ligningen
mellem x og y. Denne formel er ikke meget kendt i dag, hvor man bruger andre metoder til tangentbestemmelse. |  |
C. Newtons valg af symboler
Newton valgte at betegne differentialkvotienten af en variabel x med 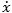 . Da Newton opfattede tiden som den eneste
uafhængige variabel, var det underforstået, at der var tale om differentiation mht. tiden. Denne begrænsning viste sig at være
en alvorlig mangel ved Newtons priksymbol. Symbolet bruges stadig i lærebøger og artikler, men vist kun i situationer, hvor
den uafhængige variabel er tiden.
. Da Newton opfattede tiden som den eneste
uafhængige variabel, var det underforstået, at der var tale om differentiation mht. tiden. Denne begrænsning viste sig at være
en alvorlig mangel ved Newtons priksymbol. Symbolet bruges stadig i lærebøger og artikler, men vist kun i situationer, hvor
den uafhængige variabel er tiden.
Newton benyttede ikke noget specielt symbol for integration, han brugte ordet kvadratur i stedet. Det spiller naturligvis ingen større rolle i en integraltabel, som den, der er vist ovenfor. Men når man kommer til at formulere regler for integration, er det en alvorlig mangel, at operationen ikke betegnes med et velegnet symbol.
D. Primært og ultimativt forhold
Vi slutter denne omtale af Newtons matematik med en kort beskrivelse af Newtons forsøg på at undgå at bruge uendelig små tal. Det var en kritik, som tidens matematikere fandt berettiget. Men de tog det nogenlunde roligt, fordi de ved hjælp af differential- og integralregning fandt en masse resultater, f.eks arealer, buelængder, krumninger og tyngdepunkter, hvis rigtighed var ubestridelig.
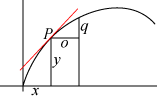 | Newtons udgangspunkt var tangentbestemmelse. Han bestemte hældningen af den røde tangent til en kurve i et punkt P med koordinater (x,y) ved at give x en lille tilvækst o. Den tilsvarende y-tilvækst betegner vi q og forholdet α = q/o er da en tilnærmelse til den søgte tangenthældning. På Newtons tid ville nogen sige, at hvis man valgte o uendelig lille, men dog ikke 0, da vil forholdet være lig med tangenthældningen. Problemet er, om der findes så små tal? For at undgå sådanne tal definerer Newton to (ens) nye værdier af dette forhold. Det "ultimative" forhold fremkommer når man i tidens løb gør o mindre og mindre indtil den til sidst er 0. Forholdet kaldes da "ultimativt" lige før o bliver 0. Hvis vi omvendt starter med o = 0 og så lader tiden gå så o vokser, så er forholdet "primært" lige efter at o var nul. Newton siger, at de to forhold er lige store og lig tangenthældningen. |
I dag vil vi nok sige, at der også i denne beskrivelse optræder uendelig små tal, hvad er ellers "lige før" og
"lige efter"? Newton må have
haft det bedre med at bruge uendelig små tidsintervaller, for tiden går jo rent faktisk, det gør tallene ikke. - Minder
det ikke om de gamle grækeres
afvisning af tallene, fordi længden af diagonalen i et enhedskvadrat ikke kunne angives med et rationalt tal?
3. Om Leibniz´ differential- og integralregning.
Leibniz kom til Paris i 1672 på en lidet krævende mission som diplomat. Han vidste på det tidspunkt ikke meget om matematik, men Huygens, der også var i Paris på det tidspunkt, opdagede hans evner og vejledte ham i den højere matematik. Det resulterede i, at Leibniz skabte sin version af differential- og integralregningen i 1675 og de følgende år, og da han vendte tilbage til Hannover, skabte han en livlig forskningsmæssig aktivitet på Kontinentet.
A. Kvadraturer og tangenthældninger som summer og differenser
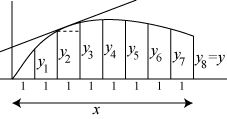 |
Figuren til venstre illustrerer Leibniz´ opfattelse. Den kurve y, der skal undersøges, forbindes med den vandrette akse med
en række lodrette liniestykker. To vilkårlige naboliniestykker har afstanden 1.
Hvis enheden er lille er kurvens kvadratur (dvs. arealet under kurven) med god tilnærmelse summen af y - erne, altså y1 + y2 + y3 + ... + y8, og hvis enheden er valgt uendelig lille er kvadraturen lig med summen. På lignende måde er tangenthældningerne med god tilnærmelse differens mellem to på hinanden følgende y - er. F.eks har den tegnede tangent med god tilnærmelse hældningen y3 - y2, og hvis enheden er valgt uendelig lille er tangenthældningen lig med denne differens. |
På baggrund af disse to observationer opdagede Leibniz analysens hovedsætning. Den siger, at bestemmelse af kvadratur og bestemmelse af tangenthældning er inverse operationer. Det betyder to ting:
1. Kvadraturen er bestemt af x - værdien, så man kan opfatte kvadraturen som en ny variabel z, der afhænger af x. Tangenthældningen for denne variabel er y, nemlig den tilvækst kvadraturen får, når x får tilvæksten 1. Tangenthældningen for kvadraturen for en kurve y er altså y selv. I dag ville vi udtrykke denne erkendelse i formlen
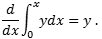
2. Tangenthældningen for kurven y på figuren er differensen mellem en y-værdi og den foregående. Kvadraturen af tangenthældningen er summen af disse differenser, altså
(y1 - 0) + (y2 - y1) + (y3 - y2) + ··· + (y8 - y7) = y8 .
Heraf følger, at kvadraturen af tangenthældningen af en kurve y er y selv. I dag ville vi udtrykke denne erkendelse i formlen
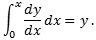
Disse to resultater udsiger tilsammen, at bestemmelse af tangenthældning og kvadraturbestemmelse er inverse operationer. Det betyder, at når man starter med en kurve y og udfører de to operationer efter hinanden, så bliver resultatet y.
Leibniz lagde vægt på, at mens kvadraturen, (altså summen y1 + y2 +
y3 + ... + y8) kan være svær at udregne, er det let at udregne
tangenthældningen som differens mellem to på hinanden følgende y-værdier.
B. Leibniz´ valg af symboler
Leibniz skabte grundlaget for sin differential- og integralregning i en kort periode i 1675, nemlig fra 25. oktober til 11. november. Det var et grundlæggende princip for Leibniz, at han ville vælge hensigtsmæssige symboler for differentiation og integration, og på den baggrund formulere overskuelige regneregler for dem.
Leibniz startede med at betegne kvadraturen, altså arealet under en kurve y for omn.y. Han fortæller selv, at omn. er en forkortelse af "omnes lineae", "alle linier". Han tænkte på summen af linierne, nemlig y-erne på figuren ovenfor. Han var imidlertid ikke tilfreds med navnet, måske fordi det ikke antyder, at der er tale om en sum. Han skriver: "det vil være nyttigt at skrive ∫ i stedet for omn, således at ∫ l betyder summen af alle linierne l." Hermed er integraltegnet introduceret. Symbolet ∫ er en af de måder man skrev et kursiveret s på på Leibniz´ tid.
Da differentiation er bestemmelse af tangenthældning, altså som vi så en differensdannelse, bestemte Leibniz sig til at markere differentiation med et d. Efter nogle ikke så vellykkede forsøg valgte Leibniz at betegne differentialkvotienten af en variabel y med dy og han fandt hurtigt formlen for differentiation af et produkt,
d(uv) = u dv + v du.
Lidt senere fandt Leibniz ud af at det var endnu mere hensigtsmæssigt at betegne tangenthældningen for kurven y med uafhængig variabel x med dy/dx. Tangenthældningen er jo forholdet mellem en lille y-tilvækst dy og den tilsvarende x-tilvækst dx. Disse små størrelser kaldes differentialer, og deres forhold fortjener derfor navnet differentialkvotient. I vore dage ville man udtrykke det lidt anderledes: De små tilvækster er differenser og betegnes Δx og Δy. Deres forhold Δy/Δx kaldes en differenskvotient, og differentialkvotienten er dennes grænseværdi når Δx → 0. Det er egentlig ikke overraskende, at man tit kan regne med dy/dx som om det var en almindel brøk. F.eks. siger reglen om differentiation af en sammensat funktion at dz/dx = dz/dy · dy/dx.
Med den nye navngivning nævner Leibniz straks, at
∫ x = ½ x2
og i det fortsatte arbejde finder han en lang række af de almindelige formler for differentiation og integration. Under dette arbejde indså han, at det var hensigtsmæssiget at skrive f.eks. ∫ ydx i stedet for blot ∫ y. ∫ ydx er jo sum af en masse produkter af formen y·dx hvor dx er en uendelig lille tilvækst til x.
Leibniz´ første artikel om differential- og integralregning kom i 1684. Den var ikke særlig pædagogisk, og det var af stor betydning
for udbredelsen af kendskabet til især differentialregning, at l´Hospital i 1696 udgav sin lærebog i differentialregning.
l´Hospitals bog byggede i
vid udstrækning på hans samarbejde med Johann Bernoulli.
| Hvis du støder på et ord, hvis betydning du ikke kender, så søg på ordet. |