|
Forside
Søgning
Liste |  |
Gravitationsloven
1. Indledning
Gravitationsloven (eller tyngdeloven) er menneskeskabt, men den kan på ingen måde siges alene
at være et produkt
af Newtons genialitet.
I 1625 tyngdekraft har vi
forklaret, at tyngdeloven er
et resultat af en lang udvikling, hvis detaljer vi ikke kan komme ind på her. Vi nævner dog, at flere
fysikere, deriblandt Hooke, havde foreslået en tyngdekraft, hvis styrke var omvendt proportional med
kvadratet på afstanden a. En af inspirationskilderne til dette synspunkt var sandsynligvis den tilsvarende lov
for lysstyrke, bl.a. formuleret af Kepler i 1612. I 1666 havde Newton
kendskab til formlen for accelerationen i en jævn cirkelbevægelse, og han havde påvist det, i denne sammenhæng
meget vigtige, faktum, at det af Keplers
love følger, at planeternes acceleration er rettet mod Solen, og i størrelse er omvendt proportional med
kvadratet på afstanden til Solen. Det er et vægtigt argument, for at gravitationsloven har
et a2 i nævneren. Newton var også klar over, at hvis tyngdeloven
har et a2 i nævneren, da bliver planetbanerne ellipser med Solen
i det ene brændpunkt. Det var hans formodning, at
Galileis faldlove er et specialtilfælde, og at planeternes bevægelser kan beregnes
ved brug af loven. Men han manglede et afgørende bevis for, at den samme lov kunne bruges både på
Jordens overflade og ude i Månens afstand.
Et æbles fald fra et træ og Månens bevægelse på himlen skulle altså kunne beskrives af samme lovmæssighed. Det fremgår af en bemærkning af Newton, at han anså en påvisning af dette for at være en afgørende test af teoriens holdbarhed.
2. Gennembruddet
På det tidspunkt kendte man ikke Jordens radius med acceptabel nøjagtighed, og Newton kunne
derfor ikke få tallene til at stemme, og han droppede foreløbig sagen. I 1682
hørte han så et fordrag i Royal Society om en ny måling af Jordens radius, udført af franskmanden
Jean Picard. Picard
havde (omsat til km) målt radius
til 6329 km, (hvilket er under ½ % forkert). Nu kunne Newton udføre testen.
Vi udregner først Månens acceleration. I 1659 havde Huygens fundet ud af, at Månens acceleration er
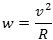
Her betyder v Månens fart, og R dens afstand fra Jordens centrum. Vi bruger nu enhederne
meter og sekund. Da R er 60 jordradier, fås, at
R = 60·6329000 = 3,80·108 m. Månens omløbstid er
27,32 døgn = 27,32·24·3600 sek. = 2,36·106 sek. Længden af
månebanens cirkel er L = 2πR = 23,88·108 m. Derfor er
v = 23,88/2,36·102 = 1012 m/sek., og Månens acceleration
bliver derfor
w = v2/R = 10122/3,8·108 =2,70 ·10-3 m/sek2.
Her på Jorden er tyngdeaccelerationen som bekendt
g = 9,81 m/sek2
Da Månen er 60 gange så langt væk fra jordcentret som en iagttager på jordoverfladen, er
Newtons forventning at g = 602·w. Ved udregning fås, at
602·w = 9,72 m/sek2. I betragtning af
usikkerheden på Månens afstand, er det en fuldt tilfredsstillende overenstemmelse. Newton udtrykte
sin tilfredshed med sit resultat ved at udtale, at
| Lunam gravitare in Terram et vi gravitatis retrahi semper a motu rectilinio et in orbe suo retineri. |
dvs. "... at Månen har tyngde i retning mod Jorden, og at den ved denne tyngdes kraft altid trækkes væk fra en retlinet bevægelse og holdes tilbage i sin egen kreds."
3. Gravitationsloven
Vi går nu over til at betragte Newtons gravitationslov i sin helhed. Den siger, at to partikler
med masser m1 og m2
og afstand a påvirker hinanden med en tyngdekraft F af størrelsen
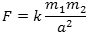
Tyngdekraften på den ene partikel peger på den anden. k er en universel konstant, hvis værdi kun afhænger af de valgte enheder. Værdien af konstanten k må findes ved måling af tiltrækningen mellem to kendte masser. Det er en meget vanskelig måling, der først rigtigt lykkedes for Cavendish i 1798. Kraftenheden newton (N) defineres som den kraft, der giver et lod på 1 kg en acceleration på 1 m/sek2. Da tyngdeaccelerationen er ca. 10 m/sek2 er tyngdekraften på loddet ca. 10 newton. 1 newton er derfor ca. tyngdekraften på et lod på 100 g. Bruges enhederne m, sek, kg og N, får k værdien 6,7·10-11. Det viser, at tyngdepåvirkningen mellem almindelige legemer her på Jorden er forsvindende. Vi kalder k for Newtons konstant.
Vi fremhæver, at værdien af tyngdeloven i første omgang viste sig ved, at man kunne beregne planeternes banebevægelser med en fornuftig nøjagtighed ved brug af tyngdeloven og Newtons bevægelseslove. (Se nærmere om det under Newton og Keplers love, 1687.) I dag bruges gravitationsloven flittigt i forbindelse med rumfart og satellitnavigation.
Newton foretog omfattende beregninger på baggrund af tyngdeloven. En af de ting, han fandt ud af, handlede om en kugle, der består af homogene koncentriske kugleskaller, hvilket specielt gælder, hvis den er ens hele vejen igennem. Newton beviste (- se beviset i den anden linie 1682 Newton), at hvis man flytter hele massen af en sådan kugle til dens centrum, da ændrer man ikke tyngdekraften uden for kuglen. Det brugte vi i argumentet om Månen og æblet ovenfor.
4. Solens og de månebærende planeters masser
Tyngdeloven udtrykker tyngdekraften ved de to masser og deres afstand. Men den muliggør også bestemmelse af den ene masse, når den anden, afstanden og tyngdekraften kendes. Denne ide brugte Newton til at bestemme forholdet mellem Solens masse S og Jordens masse J. Vi gengiver her argumentet fra la Cour.
Til venstre på figuren nedenfor viser vi Jorden med masse J i sin bane om Solen med masse
S. Vi bruger månebanens radius som længdeenhed, så bliver jordbanens radius 390. Til højre viser vi
Månen i sin bane om Jorden og desuden en tænkt måne med masse Z, der bevæger sig om Jorden i en bane,
der også har radius 390. Omløbstiderne i døgn er også vist på figurerne. Z gennemløber sin bane
på x døgn. Dette x kan bestemmes af Keplers 3. lov:
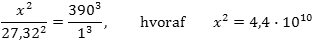
På figurerne viser vi også hastigheder v og accelerationer w for Jorden til venstre og for Z til højre.
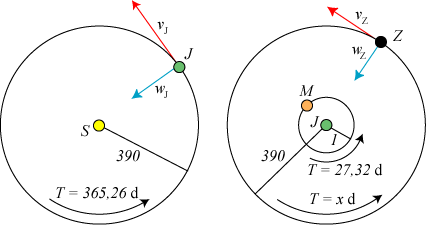
Vi bruger nu Newtons 2. lov og gravitationsloven på Jorden til venstre og på Z til højre:

Heraf fås ved division, at
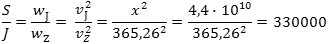
Her følger det andet lighedstegn af Huygens´ formel for accelerationen i en jævn cirkelbevægelse (w = v2/R), og det tredje lighedstegn følger af, at omløbshastighederne forholder sig omvendt af omløbstiderne.
Solen vejer altså 330.000 gange så meget som Jorden.
Nøjagtigheden af resultatet afhænger især af, hvor nøjagtigt afstanden til Solen er kendt. Her har vi brugt et tal, der først blev kendt efter en venuspassage i 1769.
På Newtons tid kendte man de relative afstande og omløbstiderne for de fire dengang kendte jupitermåner. Det var derfor let at eftervise, at Keplers tredie lov også gælder for Jupiter og dens måner. Dette forhold var vigtigt for Newton. Det viser nemlig, at gravitationen ikke kun er knyttet til Solen, men at den også virker på Jupiter. På den baggrund kunne Newton hævde, at gravitationen er en almen naturkraft, der virker mellem to vilkårlige legemer.
Den yderste af Jupiters 4 gammelkendte måner er 5 gange så langt fra Jupiter, som vores måne er fra os.
Ved at opfinde en tænkt måne om Jorden ude i den afstand, kan man på tilsvarende måde regne ud, at Jupiter
vejer 310 gange så meget som Jorden. På den måde fandt Newton massen af Mars, Jupiter og Saturn målt med
Jordens masse som enhed. For fuldstændighedens skyld følger her en tabel over planeternes masser, sådan som
de kendes i dag. Enheden er Jordens masse, som vi nu ved er 6·1024 kg.
| PLANET | Merkur | Venus | Jorden | Mars | Jupiter | Saturn | Uranus | Neptun | Pluto |
| MASSE | 0,055 | 0,81 | 1 | 0,107 | 318 | 95 | 14,6 | 17,1 | 0,0002 |
6. Konklusion
Det er et fantastisk fremskridt i menneskehedens
historie, at man kan finde ud af den slags og ikke må overlade det til uvidenhed og overtro.
| Hvis du støder på et ord, hvis betydning du ikke kender, så søg på ordet. |