1. Newtons 2. lov

Vi starter med Newtons 2. lov. Den siger, at

Formlen siger dels, at kraftvektoren F og accelerationsvektoren w har samme retning, og dels, at de tre størrelser er forbundet af ligningen F = m·w

Med denne ligning indfører Newton endeligt de to begreber kraft og masse. Begreberne havde ligget i luften i århundreder, men først nu får de et forpligtende indhold. Newtons definitioner er ikke særlig klare, og nedenfor prøver vi at forklare begreberne i mere moderne sprog.

Vi har ovenfor brugt ordet partikel i stedet for legeme. Mens forskellige dele af et fast legeme godt kan have forskellige hastigheder og forskellige accelerationer, er en partikel et legeme, der er praktisk talt punktformet. En partikel har altså én bestemt hastighed og én bestemt acceleration. En partikel har en masse. Hvis den ikke har en masse, taler man om et punkt.

2. Om begrebet masse

Begrebet vægt er knyttet til Jordens overflade, og vægten af et legeme afhænger af omgivelserne. F.eks. af, om det befinder sig i luft, i et lufttomt rum eller i vand. På Månen vejer en ting kun en sjettedel af, hvad den vejer her på Jorden, og ude i verdensrummet er det svært at veje noget som helst på en vægt. Men når man nu skal beskrive en sammenhæng mellem en kraft og den acceleration, den giver legemet, så må der nødvendigvis et eller andet vægtagtigt ind i billedet. Og det er det, som bliver kaldt masse.

Det er en ved talrige forsøg bekræftet kendsgerning, at hvis to legemer har samme vægt, så har de også samme masse, dvs., at så får de samme acceleration, når de påvirkes ensartet. Mange af disse forsøg blev lavet af Newton selv. Han lavede to lige lange og lige tunge (og, af hensyn til luftmodstanden, lige store) penduler af forskellige materialer og efterprøvede, at de har samme svingningstid. Det ville de jo ikke have, hvis de på trods af ens vægt havde forskellig masse og dermed forskellig tyngdeacceleration. Partikler med samme vægt har altså samme masse. Vi definerer derfor et legemes masse som den vægt, vi finder, hvis vi vejer den med en almindelig vægt her på jordoverfladen. Hvis man skal være meget omhyggelig, skal man, af hensyn til at Jorden er lidt fladtrykt, vælge et bestemt sted, f.eks. Paris. Og hvis man skal være endnu mere omhyggelig, skal vejningen foregå i et lufttomt rum, så opdriften i luften ikke får betydning. Så får selv en tivoliballon positiv masse, selv om den har negativ vægt.

Men lad os slå fast: Det er ikke en trivialitet, at når en partikel er tungere end en anden, da er den også sværere at accelerere end den anden.

3. Kræfter

Også begrebet kraft var der mange forudanelser om i århundrederne før Newton. En kraft er en påvirkning af en partikel, der ændrer dens hastighed. Som en (næsten udtømmende) række eksempler på kræfter kan nævnes: Fjederkræfter, gnidningsmodstand, magnetiske og elektriske kræfter og gravitationskræfter. Kræfter kan f.eks. måles i den enhed, der hedder newton, forkortet N. 1 newton defineres som den kraft, der giver en masse på 1 kg en acceleration på 1 m/sek². Definitionen bygger på den erfaring, at en konstant kraft giver en konstant acceleration. Vi går nu over til at beskrive, hvordan man kan måle størrelsen af en vilkårlig kraft.

Vi bygger et måleinstrument som vist på figuren til venstre. Føleren er en fjeder. Den sidder fast på et stativ i den ene ende. I den anden ende er der en viser, der peger på en gul skala. Når fjederen ikke er spændt, peger viseren på 0. Fjederen skal opfylde Hookes lov (1664). Det starter vi med at kontrollere: Vi tager en masse ens små lodder, og hænger dem på den nederste krog en ad gangen. Så skal vi hver gang få samme fjederforlængelse.

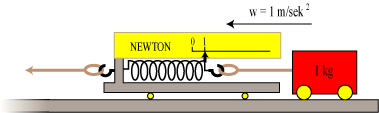
Så skal vi tegne en inddeling ind på den gule skala. Vi lægger instrumentet på ruller på et langt bord og binder en vogn på 1 kg i enden af fjederen. Så trækker vi i tovet i den anden ende af fjederen, og vi trækker præcis så meget, at vognen og stativet får en acceleration på 1 m/sek². Når det er opnået, peger viseren på et bestemt sted på den gule skala. Det sted tegner vi en inddelingsstreg og skriver 1 på den, underforstået 1 newton.

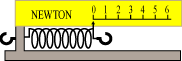Nu mangler vi så at gøre inddelingen færdig. Det gør vi, som vist på figuren til venstre, ved at vælge samme afstand mellem stregerne, som der er mellem 0 og 1. Det retfærdiggøres af Hookes lov. På billedet viser vi den færdige kraftmåler. En vilkårlig kraft kan måles ved, at man lader den virke på fjederens frie ende i forlængelse af fjederen.

Med disse definitioner har Newtons 2. lov fået en præcis mening. Når en partikel bevæger sig, kan vi på ethvert tidspunkt måle de tre størrelser F, m og w, og de passer altså hele tiden - inden for målenøjagtigheden - i ligningen F = m·w. Men det er nu ikke hovedpointen. I anvendelserne er der typisk én af størrelserne, man ikke kender. Eller der er to, man ikke kender, og dem har man en relation imellem, f.eks. tyngdeloven. Newtons 2. lov er nødvendig, når man skal beregne baner for planeter eller satellitter.

Enheden newton kan ifølge Newtons 2. lov udtrykkes ved grundenhederne således: N = kg·m/sek². Kræfter har altså dimensionen MLT^-2.

Her på jordoverfladen er tyngdeaccelerationen 9,8 m/sek². Et lod på 1 kg er derfor påvirket af en tyngdekraft på 9,8 N. 1 N er derfor tyngdekraften på et lod med massen 1/9,8 kg = 102 gram.

4. Eksempler på anvendelse af Newtons 2. lov

Vi betragter en partikel med masse m, der udfører en jævn bevægelse med fart v på en cirkel med radius R. Huygens fandt i 1659 accelerationen i bevægelsen til w = v²/R, rettet mod cirklens centrum. Partiklen er derfor påvirket af en kraft af størrelsen mv²/R, rettet mod cirklens centrum. Det er den kraft, man mærker, når man svinger en ting rundt i en snor. Jeg har lige været ude i haven og svinge en tennisbold på 60 g hurtigt rundt i en snor på 1 m. Det tog ½ sek pr. omgang på ca. 6 meter, så farten var ca. 12 m/sek. Accelerationen var derfor 144 m/sek², og kraften 144·0,06 = 8,6 N, svarende til tyngden af et lod på knap 1 kg. Det mærkedes som noget i den retning.

Eksempel 2

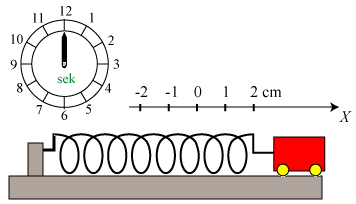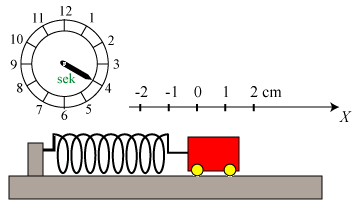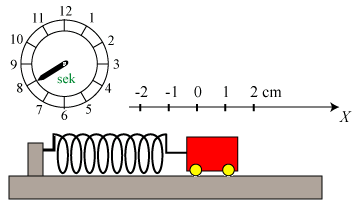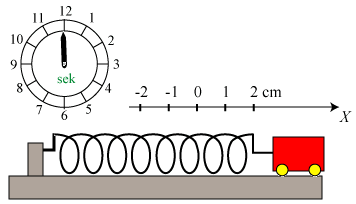
Vi tager igen udgangspunkt i Hookes lov fra 1664 om fjederkræfter. Figuren nedenfor til venstre viser en fjeder. Den er fastgjort til venstre, og den er ikke påvirket af nogen kraft. Man siger, at fjederen er i sin ligevægtsstilling, og dens længde kaldes ligevægtslængden. Den højre ende af fjederen er placeret ud for X-aksens nulpunkt. Til højre viser vi, hvad der sker, når vi påvirker fjederens højre ende med en kraft F. Det bevirker, at fjederen forlænges med et stykke x, og Hookes lov fra 1664 siger så, at forholdet k = F/x ikke afhænger af størrelsen af F. k kaldes fjederkonstanten. Den måles i newton/meter. k er den kraft, der skal bruges for, ud fra ligevægtsstillingen, at gøre fjederen 1 meter længere, så k er et mål for fjederens stivhed. Hookes lov er ikke en naturlov på samme måde som Newtons love. Det er jo klart, at der er grænser for, hvor meget man kan strække eller sammenpresse en fjeder. Men her antager vi altså, at loven gælder.

Hvis vi regner både kraften F og forlængelsen x med fortegn, gælder ligningen F = kx også med fortegn, idet F og x begge bliver negative, når fjederen gøres kortere. Som vist nedenfor til venstre fastgør vi nu en letløbende vogn med masse M i fjederens højre ende, og vi trækker vognen 2 cm til højre og holder den fast der. Vi vil nu illustrere styrken af Newtons 2. lov ved at bruge den til at finde ud af, hvordan vognen vil bevæge sig, når vi giver slip på den til tidspunktet t = 0.

Til højre viser vi situationen til et tidspunkt t. x(t) betegner altså positionen af højre ende af fjederen til tidspunktet t. Ifølge definitionen af acceleration er vognens acceleration w til tidspunktet t bestemt ved to differentiationer, w = x´´(t). Den kraft F, som fjederen påvirker vognen med, er modsat til den kraft, som vognen påvirker fjederen med, så F = -kx(t). Newtons 2. lov siger nu, at

I denne ligning er M og k kendte tal, og x(t) er en ukendt funktion. Ligningen kaldes en differentialligning, og ligninger af denne type spiller en stor rolle i fysikken. De er tit vanskelige at løse, men i vores tilfælde kan vi klare det. Vi bestemmer nu et positivt tal ω, så ω² = k/M. Så får differentialligningen formen

Det handler altså om at finde en funktion x(t), som differentieret to gange giver minus sig selv multipliceret med ω². I vores omtale af differentiation har vi nævnt, at x(t) så må have formen

og her kan man se det fornuftige i at indføre dette ω.

Da vognen kører på en ganske bestemt måde, må det være muligt at bestemme a og b. Det gør man ved at benytte de såkaldte begyndelsesbetingelser. Begyndelsesbetingelserne er her, at x(0) = 2 og at x´(0) = 0, da vognen har fart 0 for t = 0. Den første betingelse medfører, at b = 2. Derfor er

For at kunne udnytte den anden betingelse må vi differentiere funktionen:

Sætter vi her t = 0, får vi, at a = 0. Resultatet er altså, at vognens bevægelse er bestemt af formlen

Vognen svinger altså sinusformet frem og tilbage med amplituden 2 cm. Vi vil nu gerne have en svingningstid på 12 sekunder, dvs. en vinkelfrekvens, der er ω = π/6. Vi vælger altså M og k sådan, at ω får denne værdi. For dette valg af ω viser vi bevægelsen på animationen nedenfor.

Vognens hastighed v (regnet med fortegn) til tidspunktet t fås ved differentiation. v = - π/3·sin ωt, hvor ω = π/6. Farten er altså størst, når fjederen har sin ligevægtslængde, hvilket man godt kunne have forudset.

Man kan få meget at vide af denne teoretiske behandling. Uanset begyndelsesbetingelserne bestemmes vognens svingning af ligningen

Her angiver b den forlængelse, som fjederen har på starttidspunktet. Og af hastighedsformlen ovenfor følger, at starthastigheden er aω. Svingningstiden er T = 2π/ω. Svingningstiden er altså uafhængig af begyndelsesbetingelserne, og det kunne man ikke vide i forvejen. Uanset begyndelsesbetingelserne er svingningen sinusformet. Udtrykket for x(t) kan nemlig omskrives til en faseforskudt sinus, sådan som vi har nævnt det i omtalen af sinus.

Eksempel 3

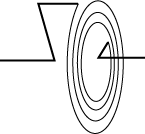Dette eksempel er en udvidelse af det foregående. Vi benytter igen en fjeder og en partikel, men denne gang er vi nødt til at antage, at fjederen har ligevægtslængde 0, ellers kan vi ikke udføre beregningerne. En fjeder med ligevægtslængde 0 kan f.eks. laves som vist på figuren, men nedenfor tegner vi den som en sædvanlig fjeder.

Figuren til højre viser det system, vi vil beskrive. En rød partikel med masse M bevæger sig i XY-planen. Vi tænker os, at planen er vandret, så vi kan se bort fra tyngdekraften. Partiklen sidder på enden af en fjeder med ligevægtslængde 0 og fjederkonstant k. Den anden ende af fjederen er fastgjort i koordinatsystemets begyndelsespunkt. Partiklen er kun påvirket af fjederkraften, og dens bevægelse er sat i gang til tidspunktet t = 0 med en begyndelsesbeliggenhed og en begyndelseshastighed, de såkaldte begyndelsesbetingelser. Ved hjælp af Newtons 2. lov vil vi nu finde ud af, hvordan partiklen bevæger sig.

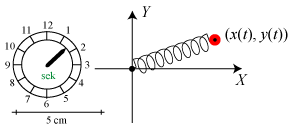Koordinaterne for partiklen til tidspunktet t betegnes (x(t), y(t)). Partiklens acceleration er så (x´´(t), y´´(t)). (x(t), y(t)) er en vektor, hvis længde er fjederens længde, og hvis retning er modsat retningen af den kraft, som fjederen påvirker partiklen med. Fjederkraften er derfor -k(x(t), y(t)), og Newtons 2. lov siger så, at

Vi indfører nu som ovenfor tallet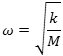

og får så, at

Nu har vi fundet to differentialligninger til bestemmelse af henholdsvis x(t) og y(t). Ligningerne er faktisk ens og magen til den ligning, vi løste i eksemplet ovenfor. Resultatet er, at

hvor a, b, c og d er konstanter, der er bestemt af begyndelsesbetingelserne. Vi har altså fundet en parameterfremstilling for banekurven.

Allerede på denne baggrund kan man sige meget om partiklens bevægelse. Bevægelsen er periodisk med periode

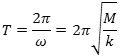
Det er overraskende, at bevægelsen er periodisk, og det er også overraskende, at perioden er uafhængig af begyndelsesbetingelserne. Som nævnt under omtalen af koordinatsystemer i 1637 fremstiller parameterfremstillingen normalt en ellipse, der er drejet i forhold til koordinatsystemet. Med specielle begyndelsesbetingelser kan det blive en cirkel eller et liniestykke, gennemløbet frem og tilbage, som vi så ovenfor.

Vi afslutter dette eksempel med at beskrive den bevægelse, der fremkommer ved et bestemt valg af de indgående størrelser. Vi vil have en periode på 12 sekunder og vælger derfor ω = π/6 sek^-1. Det kan man få for passende værdier af M og k. Så skal vi vælge begyndelsesbetingelser. Vi sørger for, at den røde partikel har koordinaterne (5,0) for t = 0, den er altså 5 cm fra koordinatsystemets begyndelsespunkt. For t = 0 er partiklens hastighed (0, π/2). Den er altså ensrettet med Y-aksen og har størrelsen π/2 cm/sek = 1,57 cm/sek. (-Dette specielle valg er truffet for at få pæne tal nedenfor). Den første betingelse giver a = 5 og c = 0. Efter en differentiation giver den anden betingelse b = 0 og dω = π/2, dvs. d = 3. Banekurvens parameterfremstilling bliver altså

Animationen nedenfor viser bevægelsen.

For t = 0 er farten π/2 = 1,57 cm/sek. I de første 3 sekunder øges farten, fordi fjederkraftens komposant i ellipsetangentens retning går i bevægelsens retning. For t = 3 er farten maksimal, den er 5π/6 = 2,62 cm/sek. I de næste 3 sekunder går fjederkraftens komposant i ellipsetangentens retning modsat bevægelsens retning. Derfor aftager farten igen.

Ovenfor har vi fundet ud af, at når en partikel bevæger sig under påvirkning af en kraft, der vokser proportionalt med afstanden fra et fast punkt O, da bliver banekurven en ellipse med centrum i O. Et andet af Newtons resultater var, at når en partikel bevæger sig under påvirkning af en kraft, der aftager omvendt proportionalt med kvadratet på afstanden fra O, da bliver banekurven en ellipse (eller et andet keglesnit) med et brændpunkt i O. Det er uventet, at det bliver ellipser begge gange.

5. Newtons 1. lov

Newtons 1. lov siger, at

Loven kaldes inertiens lov, og bevægelser, som foregår uden kraftpåvirkning, kaldes inertialbevægelser. Loven havde mange forgængere i de foregående århundreder. Galilei havde f.eks. også loven, men han anså også en jævn cirkelbevægelse for at være mulig uden kraftpåvirkning. Måske tænkte han specielt på planeternes banebevægelser i denne sammenhæng. I oldtiden og middelalderen var det almindeligt at sige, at hvis et legeme ikke blev påvirket udefra, ville det gå i stå. Det er interessant at tænke over denne modsætning. De gamle havde jo ret. Hvis motoren stopper, standser bilen. Den fejl, de begik, hvis man bedrevidende kan tillade sig at sige sådan, var, at de betragtede den komplekse, men virkelige situation, hvor der var uundgåelige gnidningskræfter. Fysikken fik først fremdrift, da man som Galilei skabte forenklede situationer, hvor man kunne se bort fra gnidningen. - Skøjteløbere er bedst til at mærke inertiens lov.

6. Newtons 3. lov

Newtons 3. lov siger, at

Man formulerer undertiden kort Newtons tredie lov ved at sige, at aktion er lig reaktion.

Eksempel 1

Et af de forsøg, som Newton lavede for at teste loven, er vist på figuren nedenfor.

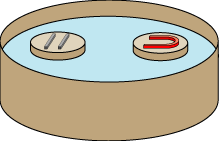Newton placerede en magnet og noget jern på to ens flydere i et kar med vand. Og så iagttog han, at de to flydere bevægede sig hen mod hinanden med samme hastighed. Magneten trækker altså lige så meget i jernet, som jernet trækker i magneten. Gad vist, om det har nogen betydning, om jernet vejer lige så meget som magneten?

Eksempel 2

I litteraturen nævnes følgende overraskende eksempel på Newtons 3. lov: Når to partier trækker tov, trækker de på ethvert tidspunkt lige meget i tovet. Tovet er jo lige stramt i begge ender. Det er en sandhed med en lille modifikation: Hvis tovet har en masse, må vinderne på et tidspunkt have påvirket tovet med en større kraft end taberne. Ellers kunne tovet jo ikke accelerere i vindernes retning.

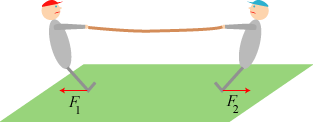Men hvis tovet nu er så let, at man kan se bort fra dets masse, så er det rigtigt nok, at vindere og tabere på ethvert tidspunkt trækker lige meget i tovet. Hvem er det så, der vinder? Det, der sker, er, at begge partier sætter hælene i græplænen og skubber til den ind mod midten. Og så skubber græsplænen lige så stærkt på personerne med kræfter F1 og F2, der er rettet udad. Og hvis så rødt hold sætter hælene mest i, er F1 > F2. Og så er hele legemet, bestående af de to personer og tovet, påvirket af en resulterende kraft af størrelsen F1 - F2 , rettet mod venstre, og så accelererer legemet mod venstre. Det er altså dem, der sætter hælene mest i, der vinder.

Eksempel 3

Newton havde også et argument, der handler om to legemer A og B, der tiltrækker hinanden: " Lad os antage, at en opstillet forhindring forhindrer to legemer, der tiltrækker hinanden, i at mødes. Hvis så legemet A bliver tiltrukket stærkere mod B end B mod A, så vil forhindringen blive påvirket stærkere fra A end fra B. Forhindringen vil derfor ikke forblive i ligevægt, men det stærkeste pres vil dominere, og det vil få systemet af de to legemer og forhindringen til at bevæge sig den vej, B ligger. Og i det åbne rum vil dette fortsætte i det uendelige i en stadig accelereret bevægelse. Dette er absurd og i modstrid med den 1. lov. For af den 1. lov følger, at systemet vil bevare sin tilstand, enten hvile eller jævn bevægelse på en ret linie. Derfor må legemerne presse lige meget på forhindringen og blive tiltrukket lige meget af hinanden."

7. Afrunding

Newtons tre bevægelseslove danner sammen med gravitationsloven et solidt fundament for mekanikkens videre udvikling. Lovene er stadig aktuelle, det er dem, man bruger, når man beregner satellitbaner, og når man planlægger en rumfart. Herunder følger en opgave med et eksempel på, at når man kender Newtons og Huygens grundlæggende resultater, da kan mange spørgsmål i mekanikken besvares. Eksemplet her har jeg fra gymnasielærer Steffen Samsøe.

Opgave 5 Vi tænker os at ballongyngen i Tivoli drejer jævnt rundt, og at de kurve, man sidder i, hænger lodret nedad hele tiden. En passager i ballongyngen har fået den sære ide, at medtage sin personvægt og stille sig på den under turen. Vil vægten så stå på det samme hele tiden?

Hvis du støder på et ord, hvis betydning du ikke kender, så søg på ordet.