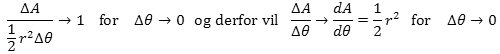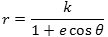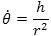Keplers areallov og afstandskvadratloven i polære koordinater

Som man kan se under 1684 Newton, er det bevis, som Newton publicerede for afstandskvadratloven, overordentlig kompliceret. Her viser vi, at loven kan udledes meget lettere, når man arbejder i polære koordinater. Det er også let at vise, at når Keplers areallov gælder, da vil accelerationen være rettet mod det faste punkt O. Vi starter med det sidstnævnte.

1. Arealloven

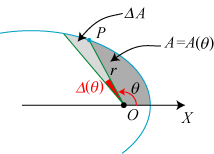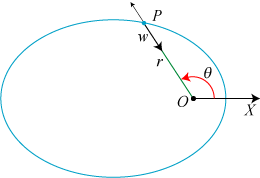
På figuren til venstre viser vi et polært koordinatsystem med begyndelsespunkt O og polarakse X. Den blå kurve har parameterfremstillingen OP: (r, θ) = (r(t), θ(t)). Det mørkegrå areal A = A(θ) overstryges af liniestykket OP, når vinklen fra X-aksen til OP varierer fra 0 til θ. Vi vil finde differentialkvotienten A´(θ). Vi giver θ en lille tilvækst Δθ, og A får derved en tilvækst ΔA som er vist lysegråt på figuren. Når Δθ → 0 vil det lysegrå område nærme sig til at være en ligebenet trekant med 2 sider af længden r, der danner en vinkel af størrelsen Δθ. Heraf følger, at

Arealet A er en funktion af t, som man kan opfatte som sammensat af funktionen A = A(θ) og funktionen θ(t). Vi bruger nu reglen om differentiation af en sammensat funktion til at finde arealhastigheden A´(t). Prik over er Newtons betegnelse for differentiation mht. tiden.

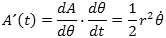
Her er både r og θ med prik over funktioner af tiden. Vi forudsætter nu i overensstemmelse med Keplers 2. lov, at arealhastigheden A´(t) er en konstant som vi kalder ½h,

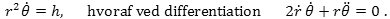
Denne formel har en uventet konsekvens. For i omtalen af polære koordinatsystemer så vi, at accelerationen for bevægelsen er

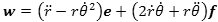
Her betyder e en enhedsvektor, der danner vinklen θ med X-aksen, og  f betyder dens tværvektor. Det at arealhastigheden er konstant medfører altså at koefficienten til  f  er 0. Da en accelerationsvektor altid peger ind mod banekurvens hulhed, har vi vist følgende resultat:

Når arealhastigheden mht. et punkt O er konstant, vil accelerationen hele tiden være rettet mod punktet O

Hvis kurven ikke vender den hule side ind mod O bliver w<0. Accelerationsvektoren peger så væk fra O. Regningerne viser også, at den omvendte sætning gælder.

Det er interessant at sammenligne dette matematiske bevis med det mere anskuelige bevis for samme sag, som du kan se i 1684 Newton. Hvor det i beviset ovenfor fremtræder som et lille mirakel, at man ved differentiation af arealloven lige præcis får, at koefficienten til  f  bliver 0, forekommer der i det andet bevis ikke den slags mirakler.

2. Afstandskvadratloven

Vi går nu over til at vise, at hvis et punkt P bevæger sig på en ellipse med brændpunkt O på en sådan måde, at Keplers areallov gælder, da vil accelerationens størrelse være omvendt proportional med kvadratet på afstanden r = OP.

Vi vil vise, at når et punkt P bevæger sig på en ellipse med brændpunkt O, således at arealloven gælder, da er størrelsen w af accelerationen omvendt proportional med kvadratet på afstanden r = OP. Når polaraksen ligger på ellipsens storakse og har begyndelsespunkt i brændpunktet O, da er ellipsens ligning i polære koordinater Her er k = a(1 - e2), hvor a er ellipsens halve storakse og e dens excentricitet. Da arealloven gælder vil,

Når vi om lidt skal regne størrelsen w af accelerationen ud, får vi brug for dr/dθ, så den starter vi med at regne ud:

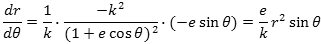
Vi skal også bruge den anden afledede af r. Den kommer her

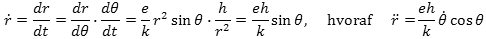
I formlen for w ovenfor er sidste led lig 0. Den med fortegn regnede størrelse af accelerationen bliver derfor

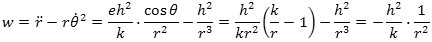
og her står jo, at accelerationen er omvendt proportional med kvadratet på afstanden r.

Det er interessant at sammenligne dette bevis med Newtons eget (1684). Beviset her kræver ingen gode ideer, men man skal kende polære koordinater. Hvis man spørger om, hvordan accelerationen afhænger af afstanden, så må man jo regne accelerationen ud og se, hvad det giver. Newtons publicerede bevis er helt anderledes. Det er ikke til at gennemskue, hvordan han har fået ideerne. Sammenligningen viser, hvilket vidunderligt hjælpemiddel differential- og integralregningen er. Det kan ikke 100% udelukkes, at Newton i første omgang har fundet resultatet, som vi har gjort her. Han kendte polære koordinater og vidste, hvordan man differentierer i polæære koordinater. Og i publikationerne foretrak han tit en græsk præget fremstillingsform frem for brug af differential- og integralregning.

Hvis du støder på et ord, hvis betydning du ikke kender, så søg på ordet.